Review: Regime-Aware Factor Allocation with Optimal Feature Selection
해당 게시글은 Bosancic et al.(2024)의 “Regime-Aware Factor Allocation with Optimal Feature Selection” 논문을 리뷰한 글입니다. 본 게시물에서 인용한 논문 및 자료에 대한 상세 정보는 아래의 링크를 통해 확인하실 수 있습니다.
Bosancic et al.(2024)
Introduction
이 논문은 기존 국면분석에 가장 많이 활용되는 은닉 마코프 모델(Hidden Marcov Model: HMM) 대신 Bemporad et al. (2017)의 statistical Jump Model을 활용하여 시장의 국면을 분할하여 팩터투자 전략을 구현했다.
이 모델은 HMM이 낮은 신호 대 잡음 비율(signal to noise ratio)과 시장의 높은 차원성, 복잡성으로 인해 상당한 거래 비용을 초래한다는 문제점을 완화한다는 장점이 존재한다.
이때 Jump Model(JM)을 구현하는데에 있어서 가장 중요한 것은 각 특성이 목표 팩터에 미치는 상대적 중요도가 시간에 따라 변화하는 것을 얼마나 반영할 수 있느냐 이다. JM 프레임워크 내에서 이러한 조건을 무시하면 시간에 따라 변화는 특성의 중요도에 적절히 대응하지 못함으로 인해 안좋은 결과가 나올 수 있다. 이에 본 논문에서는 혁신적인 최적 특성 선택 접근 방식을 활용한다. 이는 Nystrup, Kolm, and Lindström (2021)의 기존 방법을 확장하여 각 훈련 윈도우마다 최적의 feature 조합을 선택한 후 팩터 모델을 재적합하는 시점마다 업데이트하는 방식이다.
본 논문에서 보인 결과는 다음과 같다.
- 국면 인식 single-factor 전략은 국면을 분할하지 않은 단순한 buy and hold 전략을 능가한다.
- 국면 인식 multi-factor 전략은 국면을 분할하지 않은 단순한 동일 가중 멀티팩터 전략을 능가한다.
- 최적 기능 선택은 시간 국면 식별 능력을 크게 개선하고 고정되 특성 조합을 능가한다.
Methodology
데이터는 일별 데이터, 국면은 2개로 설정.(상승국면, 하락국면)
Discrete JM
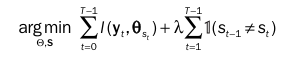
$\lambda$: 점프 패널티를 조절하는 파라미터
$y_t$: t시점의 수익률 데이터
$\theta_{S_t}$: t시점에서의 국면 중심 데이터 이 식에서 중요한 것은 손실함수인 I함수이다. 일반적으로 손실함수는 L2 norm을 사용하기 때문에 해당 논문에서도 동일한 손실함수를 적용하였다.
$\ell(y_t, \theta_{s_t}) = \frac{1}{2} | y_t - \theta_{s_t} |^2$
위 손실함수는 각 시점의 feature가 군집 중심과 가까워지도록 하여 시간 구간들을 클러스터링하는 것으로 두번째 항이 없다면 K-means 클러스터링 방법론으로 근사할 수 있다.
두번째 항은 국면의 전환을 최소화하도록 하며 $\lambda$ 값을 통해 조절할 수 있다.
이를 통해 얻어진 결과는 discrete한 국면 식별 결과를 나타낸다. 이때 각 시점에 숨겨진 상태(state)는 0 or 1로 식별된다.
Aydinhan et al. (2023)은 이렇게 칼같이 국면을 분할하여 계산하는 하드 클러스터링의 문제점을 지적하기도 했다.
Continuous JM
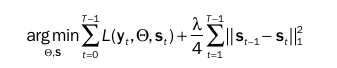
continuous JM에서의 첫번째 항도 L2 norm을 활용하여 손실함수가 구성된다. 하나의 국면에만 속한다고 가정하고 해당 국면의 파라미터로 손실함수를 계산하는 Discrete JM의 첫번째 항과 달리 여기서는 각 국면 k의 손실에 대해 해당 확률만큼 가중 평균하는 방식이다. 따라서 여러 군집에 동시에 속함을 가정하는 구조라고 할 수 있다.
두번째 항의 경우도 단순히 국면이 다르면 1, 같으면 0을 출력하는 Discrete JM과는 달리 L1 norm을 활용하여 두 확률 벡터 사이의 거리를 최소화하고 상태 전환에 다시 페널티를 주는 구조이다.
본 논문에서는 국면에 대한 클러스터링의 상대적 신뢰도 또는 강도에 대한 더 깊은 이해를 얻을 수 있다는 장점을 가지는 Continuous JM 모델을 활용하였다. 이후 국면을 분할하는 기준이 되는 기능을 위해 고정된 임곗값을 설정해주었다.
Regime Identification
본 논문에서는 각각의 팩터를 개별적으로 국면에 분할시킨다. 6개월 간격으로 모델 피팅과 매개변수 업데이트를 진행해준다.
Optimal Feature Selection
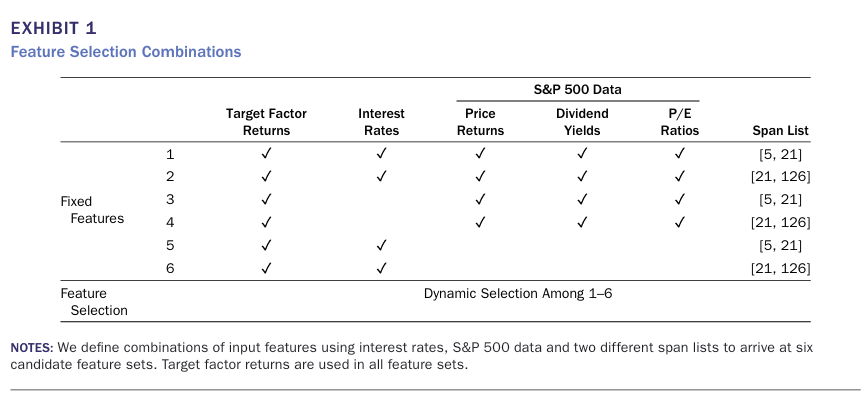
본 논문에서는 자산 조합을 구성할 때 세가지 종류의 특성 카테고리를 구성했다.
(1) 미국 금리(US interest rates)
(2) S&P 500 시장 데이터
(3) 최근 데이터의 지수 가중 이동 평균을 서로 다른 주기(span list, lookback length)에 적용한 것.
※ 본 논문에서는 국면을 통게 모델이나 기계학습을 활용하여 예측하지 않고 미래의 국면 r(t+1)을 현재 국면 r(t)로 사용한다. 예측 성능을 끌어올리는 데에는 더 효과적일 수 있지만 해당 논문에서는 간단한 국면분석만으로도 기존 전략을 능가할 수 있다는 것을 보이고자 하였다.
Portfolio Construction
- single-factor portfolio
r(t+1) = 0(성장 국면) → 보유량의 100% 해당 팩터에 할당 r(t+1) = 1(하락 국면) → 보유량의 100% 3개월 만기 미국 국채에 할당
이러한 전략과 기존 국면에 관계없이 single-factor로 buy and hold 하는 전략을 비교. 이를 통해 폭락 기간 동안 투자자를 보호하여 Max-drawdown을 줄이는 것을 목표로 한다.
- Multi-factor portfolio
이 전략은 해당 시점에 성장 국면으로 분류된 팩터들을 동일 가중치로 설정함으로써 포트폴리오를 구성한다. 이는 매일 리밸런싱되며 만약 모든 팩터에서 하락국면(crash regime)이 발생할 경우 자산 보유량의 100%를 미국 국채에 할당한다.
또한 실증 분석을 위해 1970년 1월부터 2023년 12월까지의 일일 데이터를 사용하였다.
전략에 포함될 팩터는 Momentum, Quality, Size(Small, Big), Value(Growth, Value)이다. 팩터가 선택되면 해당 팩터 기준 상위 10%를 매수함으로써 팩터 포트폴리오를 구성한다.
EMPIRICAL RESULTS
여기서는 표본 외 샘플 데이터를 활용하여 국면-팩터 전략과 단일 팩터 전략의 성과를 비교해본다.
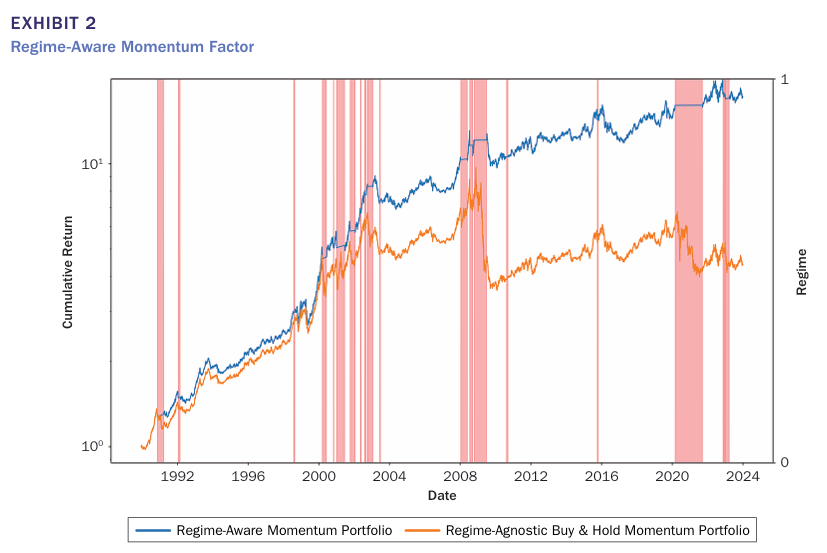
위 그림은 모멘텀 팩터에 대해 국면 포트폴리오와 기존 buy and hold 포트폴리오의 일일 누적수익률을 비교한 그래프로 국면분석을 통해 구성한 포트폴리오가 더 높은 성과를 보이고 있는 것을 알 수 있다. 이외에도 퀄리티, 밸류, 사이즈 팩터 모두 Regime-Aware Portfolio가 더 높은 성과를 기록했다. 특히 하락장에서 기존 전략은 큰 폭락을 보이는 반면 Regime-Aware Portfolio는 T-bill을 통해 폭락을 방지한 것을 알 수 있다.
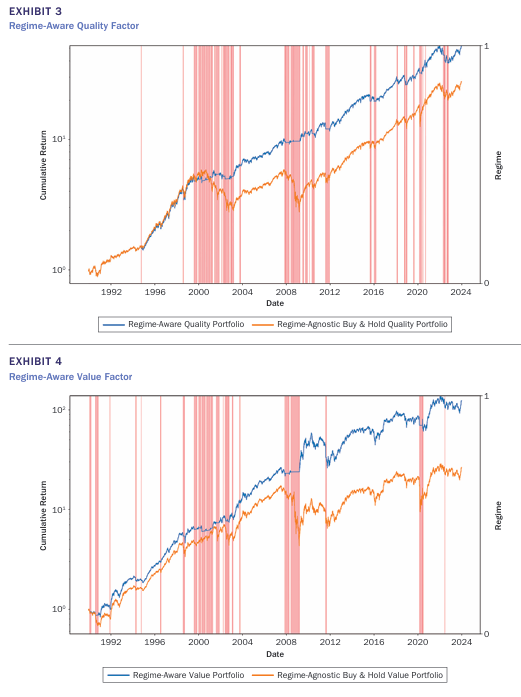
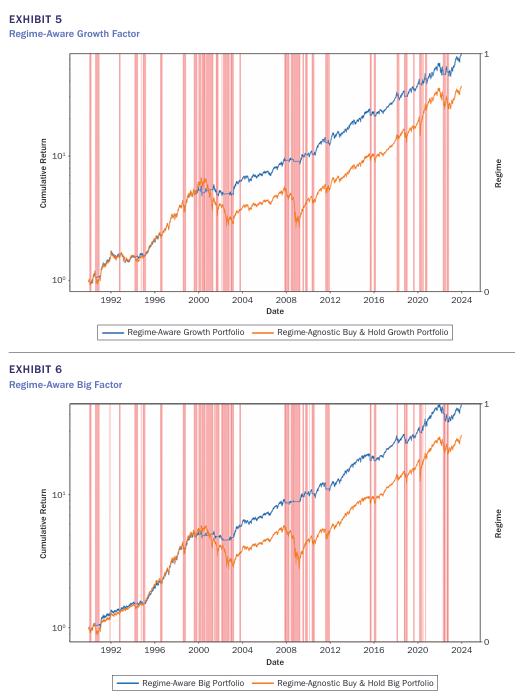
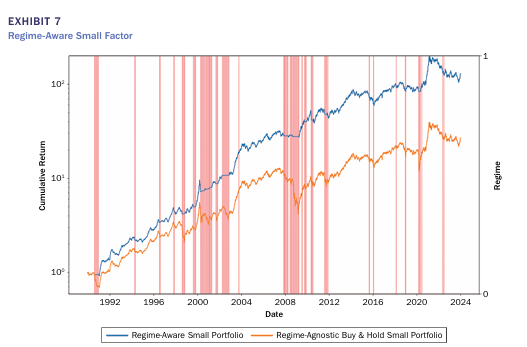
위 그림들에서 볼 수 있듯이 분홍색으로 표시된 crash regime은 2000~2002년 닷컴 버블, 2007~2008년 글로벌 금융위기, 2020년 COVID-19 기간에 나타나고 있는 것을 볼 수 있다.
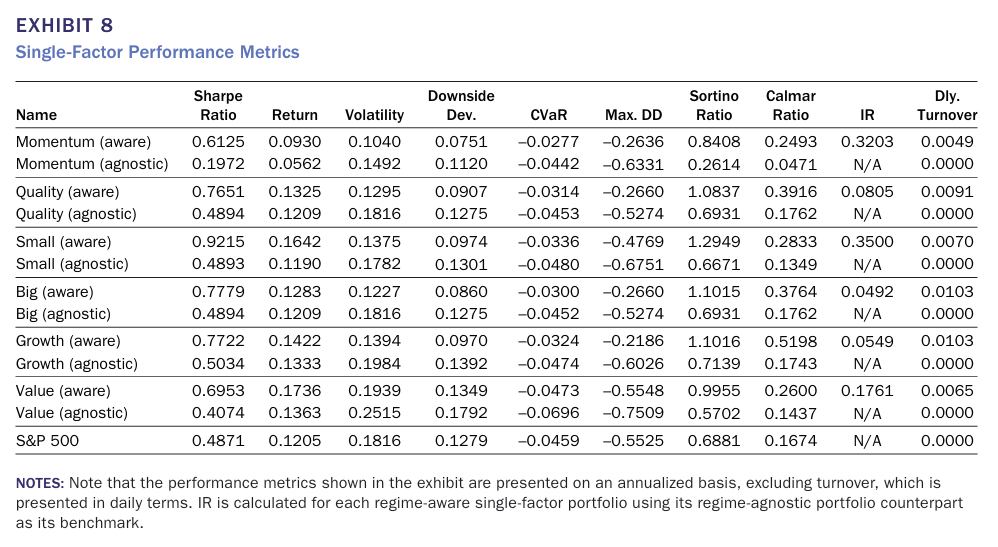
single-factor portfolio에 대해 다양한 성과 평가 지표를 통해 비교한 결과이다(annualized). 가장 일반적으로 활용되는 샤프비율의 경우 모든 팩터 포트폴리오에서 기존 Buy and hold 전략보다 높았으며, S&P500 시장 수익륣보다도 높았다.
음의 수익률만을 기준으로 성과를 측정하는 지표인 소티노 비율(Sortino Ratio) 또한 Buy and hold 전략과 S&P500 대비 높은 값을 기록했다.
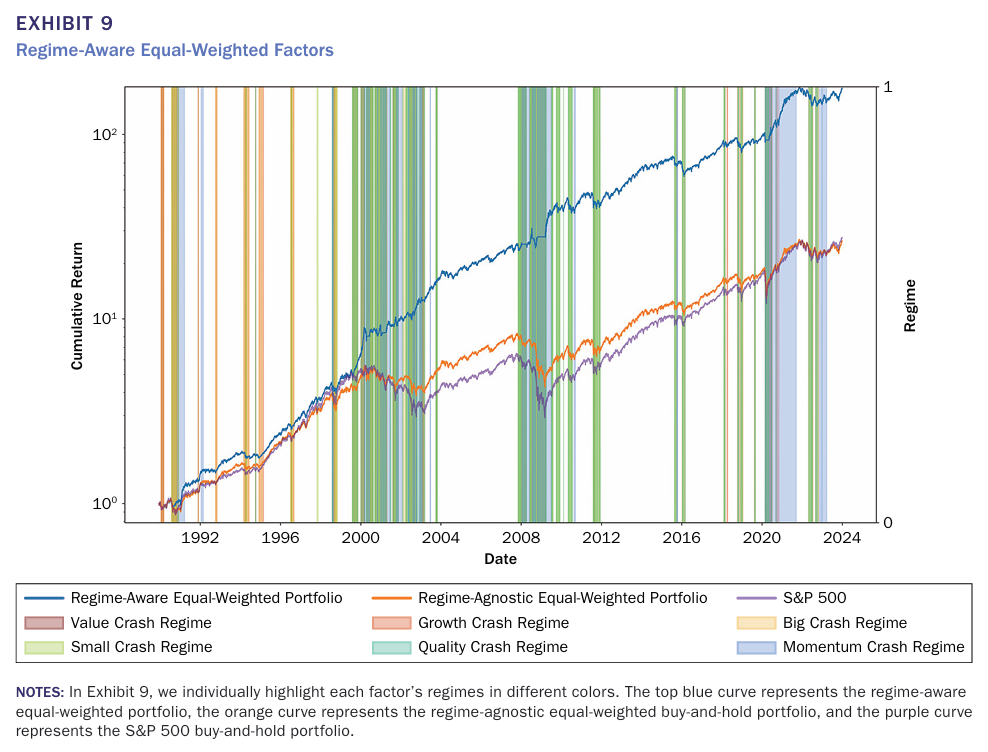
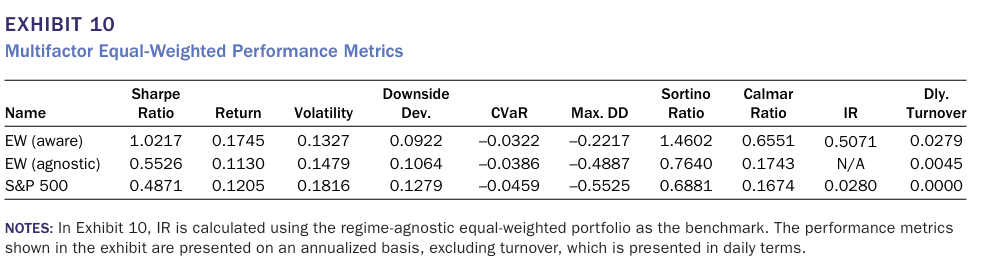
이번에는 국면 분석에 따른 멀티 팩터 포트폴리오의 성과를 나타낸 그림과 표이다.
일일누적수익률 뿐만 아니라 샤프비율, 소티오 비율, 변동성 등 다양한 지표에서 우위에 있는 것을 알 수 있다.
Fixed versus Dynamic Feature Selection
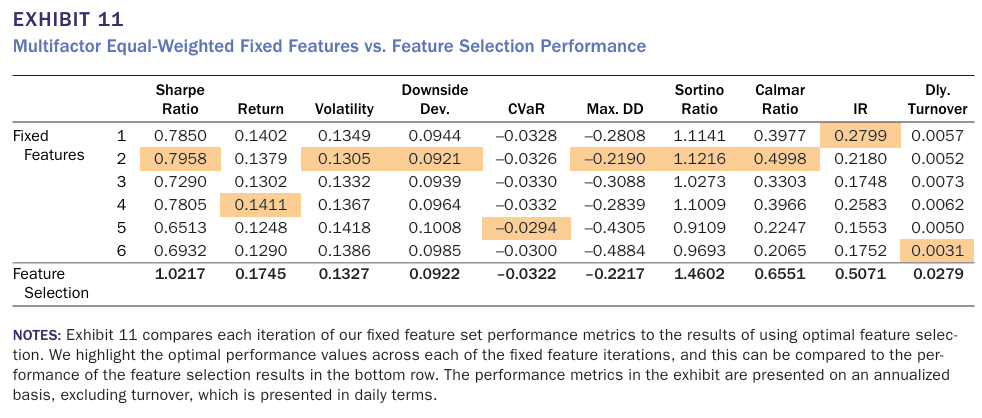
여기서는 각각의 feature들에 대해 최적의 조합을 구성하는 방법론에 대해 논의한다.
6개월마다 feature 조합을 업데이트 함으로써 고정적으로 조합을 사용하는 방식과 비교한 결과 Dynamic Feature Selection 방법이 더 높은 연간수익률, 샤프비율을 기록했다. 변동성, Max.DD 등의 지표에서는 약간 더 높은 값을 보이긴 했으나 근소한 차이기 때문에 Dynamic Feature Selection 방법이 더 효과적이라고 할 수 있다. 추가적으로 일일 매매 회전율(Dly.Turnover) 지표를 추가하여 각 전략의 리밸런싱 빈도를 분석하였는데 Dynamic Feature Selection에서 가장 높은 값을 보임을 통해 가장 자주 리밸런싱이 진행되고 있다는 것을 알 수 있다. 이는 거래비용을 반영했을 경우 수익률이 다소 감소할 수 있음을 시사한다.
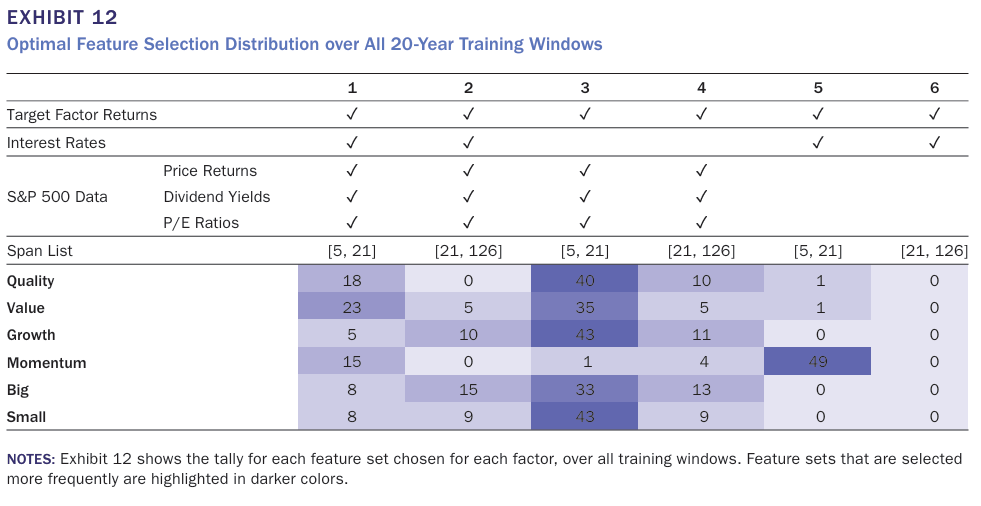
위 표는 Dynamic Feature Selection에서 각 팩터 포트폴리오가 feature 조합을 선택한 횟수를 보여주고 있다. 대부분 짧은 span list인 [5,21]을 선택하였으며 S&P 500 Data가 쓰인 조합을 반영하였으나 모멘텀 팩터의 경우 금리와 팩터수익률만을 feature로 한 조합을 압도적으로 많이 선택했다. 이를 통해 각 팩터와 시장의 근본적인 관계에 대한 어느 정도의 논평을 제공한다.
Case Study
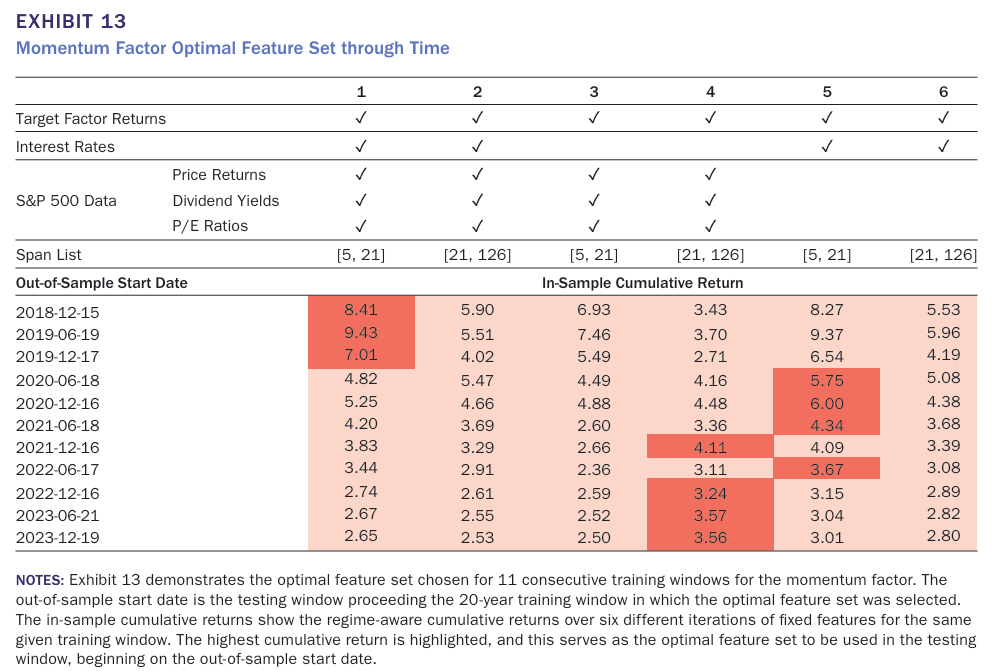
이후 모멘텀 팩터의 시간적 흐름에 따른 Dynamic Feature Selection 과정에 대해 설명한다.
2018년 12월 ~ 2023년 12월 사이의 11개 테스트 구간으로 각 테스트 구간 앞에는 20년치 훈련 데이터를 이용해서 최적 피처 조합을 선택한다.
주목할만한 점은 시장 이벤트에 따라 feature 조합이 유연하게 변동한다는 것이다. 2020년 6월, 2022년 6월에는 짧은 span과 금리 데이터만을 활용한 피쳐 조합을 선택했는데 이는 2020년 코로나 바이러스로 인해 연준에서 급격하게 금리를 인하하였기 때문으로 볼 수 있다. 반면 2021년 12월과 2022년 12월부터는 다시 S&P500 기반 feature조합을 선택하면서 금리 데이터의 정보력이 줄어들었다는 것을 보였다.
Conclusion
본 논문에서는 Statistcal Jump Model를 활용한 국면 분석과 동적으로 feature 조합을 선택하는 전략을 통해 기존 single-factor portfolio, multi-factor portfolio 대비 성과를 크게 향상시켰다.
추가적으로 이 논문의 아이디어를 기반으로 하여 랜덤 포레스트, XGBoost 등과 같은 기계학습 방법론을 활용해 국면을 예측하여 성능을 향상시키거나 다양한 포트폴리오 최적화 방법론을 활용한 multi-factor portfolio 성과 향상, 실제 투자에 활용을 위해 거래비용을 반영하여 다양한 리밸런싱 전략을 구성하는 것을 고려해볼 수 있다.