Review: Factor Momentum and the Momentum Factor

해당 게시글은 Ehsani and Linnainmaa,(2022)의 “Factor Momentum and the Momentum Factor” 논문을 리뷰한 글입니다. 본 게시물에서 인용한 논문 및 자료에 대한 상세 정보는 아래의 링크를 통해 확인하실 수 있습니다.
Ehsani and Linnainmaa,(2022)

구글스칼라에 “Factor Momentum”이라고 검색하면 가장 먼저 뜨는 3개의 논문, Arnott et al.,(2023)의 “Factor Momentum”과 Gupta and Kelly(2018)의 “Factor Momentum Everywhere”에 이어 마지막 이 논문에 대해 리뷰해보고자 한다.

1. Introduction

모멘텀은 약형 효율적 시장가설을 위반한다. 만약 자산 가격이 새로운 정보에 즉시 반응한다면 과거 수익률이 미래 수익률을 예측하는 것이 불가능하고, 이는 과거 수익률이 체계적 위험의 변화와 상관관계가 없는 한 그렇다.
지금까지 많은 연구자들이 모멘텀을 시간에 따라 변하는 위험, 행동적 편향, 거래 마찰으로 설명하려고 했지만 긴 기간과 넓은 자산 범위에서 독립적으로 작동했기 때문에 별도의 팩터로 취급되어 왔다.

※ 효율적 시장 가설?
자산 가격이 이용 가능한 정보를 얼마나 빨리 반영하느냐에 따라 3가지 형태로 나뉘는데,

1. 약형 효율적 시장가설(Weak-form)
   과거 가격, 거래량과 같은 시장 데이터는 이미 가격에 반영이 되어있기 때문에 차트 패턴 or 과거 수익률만으로는 초과수익을 지속적으로 낼 수 없다.
2. 준강형 효율적 시장가설(Semi-strong form)
   과거 가격 뿐만 아니라 재무제표, 공시, 뉴스 등의 공개된 모든 정보는 빠르게 가격에 반영되기 때문에 기본적 분석만으로는 지속적 초과수익을 낼 수 없다.
3. 강형 효율적 시장가설(Strong-form)
   공개 정보 뿐만 아니라 내부자만 아는 비공개 정보까지도 가격에 반영된다.

본 논문에서는 모멘텀이 다른 팩터를 시기별로 조정하는 동적 포트폴리오임을 보여준다.
즉 모멘텀은 다른 팩터들과 관련이 있다.

먼저 팩터의 과거 수익률이 미래 수익률에 대한 정보를 제공한다는 것을 보여주며, 이 효과는 본 논문에서 연구한 20개의 팩터에서 경제적, 통계적으로 큰 효과를 보인다.
→ 평균적으로 전년도에 수익이 있었던 경우 월 51bp를 가지지만 전년도에 손실이 있었던 경우 6bp에 불과하다. 이는 t-statistic = 4.22 로 유의하게 나타난다.

또한 본 논문에서는 Kozak, Nagel, Santosh(2018)의 투자심리 모델이 팩터 수익률의 반전 현상이나 모멘텀을 초래할 수 있으며, 이는 심리의 지속성에 따라 달라진다는 것을 보여준다.
이러한 심리가 충분히 지속된다면 팩터 수익률에도 영향을 미치게 된다.
이 모델은 모멘텀이 더 체계적인 팩터들에 집중될 것임을 예측하는데 이는 심리로 인한 수요가 상관관계를 생성해 공분산에 영향을 줌으로써 자산 가격을 왜곡시키기 때문이다.

본 논문에서는 KNS에서 제시한 47개의 팩터로부터 주성분(PC)을 추출한다. 이를 통해 팩터 모멘텀이 높은 고유값을 가지는 PC에 집중되어 있음을 발견했다.
상위 10개의 PC를 거래하는 전략은 t=6.51로 유의미한 5팩터 모델의 알파를 가진다. 이들은 다른 PC 집합의 모멘텀을 거의 흡수한다.

모멘텀이 고유값이 높은 팩터에 집중된다는 사실은 근사 차익거래 기회의 부재와 일치하는데, 만약 낮은 고유값 팩터들에서도 모멘텀이 나타난다면 차익거래자들로 인해 빠르게 사라질 가능성이 높다. Hadded, Kozak and Santosh(2020)에서 팩터의 가치 비율에 기반한 예측 가능성 또한 이와 같은 결과를 보였다.

팩터 수익률의 모멘텀은 개별 주식 수익률의 횡단면으로 전달되는데, 전달되는 양은 팩터 로딩의 분산 정도에 달려있다. 따라서 본 논문에서는 다음과 같은 가설을 검정한다.
“개별 주식 수익률은 팩터 수익률로 인해 나타나는 부분을 넘어서는 모멘텀을 보이는가?”

이 가설을 검정하기 위해 과거 1년 수익률로 정렬한 포트폴리오를 설명하는 것부터 시작한다. 결과적으로 오히려 팩터 모멘텀이 Carhart(1997)의 4-factor model의 UMD 팩터보다 과거 1년 수익률로 정렬한 포트폴리오를 더 잘 설명한다는 것을 발견했다.
GRS 검정을 통해 고유값이 큰 PC에 대한 모멘텀을 5팩터 모델에 추가하면 평균 알파가 0이라는 것을 기각하지 못한다.

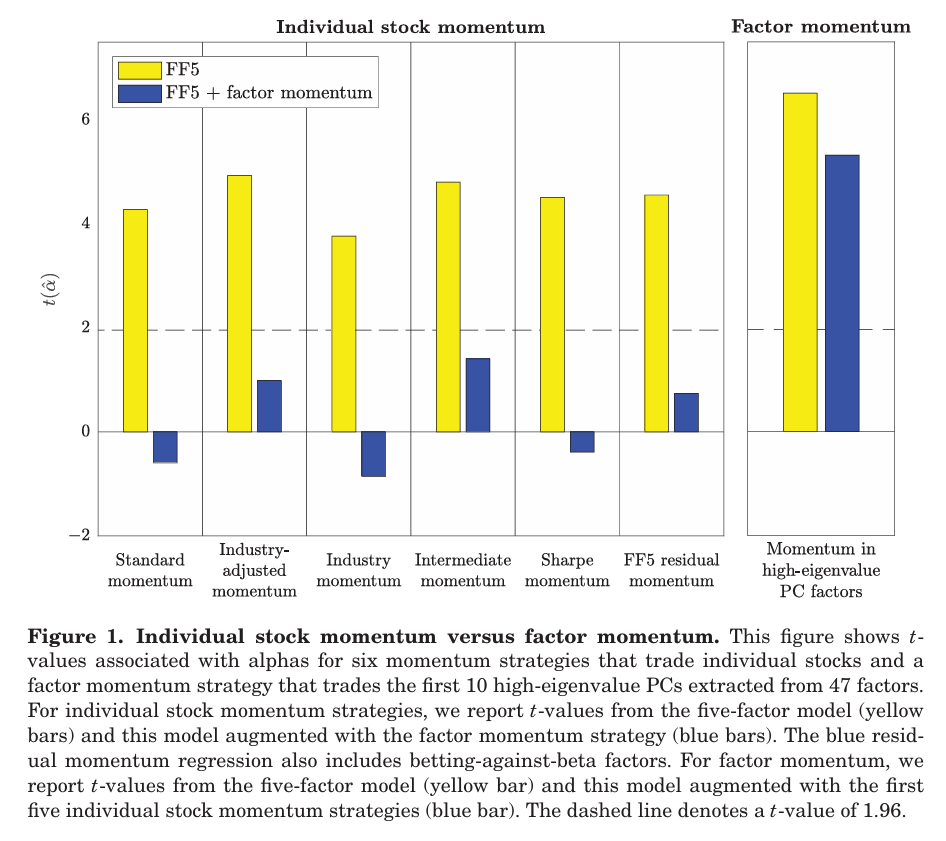
이외에도 팩터 모멘텀은 산업 모멘텀, 산업 조정 모멘텀, 중간 모멘텀, 샤프비율 모멘텀 등을 설명하는데 그림 1의 왼쪽 패널은 각 개별 주식 모멘텀에 대해 두개의 t값을 보여준다.

• 노란색 그래프는 해당 전략의 5팩터 모델에 대한 알파
• 파란색 그래프는 상위 10PC 모멘텀을 추가로 넣었을 때의 알파
• 오른쪽 패널은 이 5가지 개별 주식 모멘텀을 5팩터 모델에 추가해도 팩터 모멘텀이 여전히 유의한 t값을 가짐으로써 알파를 유지한다는 것을 보인다.

여기서 주의깊게 봐야 할 것이 바로 잔차 모멘텀인데, 잔차 모멘텀은 CAPM의 잔차를 기준으로 주식을 고르는 전략으로 과거 수익률을 기준으로 주식을 고르는 기존 모멘텀보다 더 높은 수익을 낸다. 그러나 size, value와 같은 팩터들을 통제할수록 잔차 모멘텀 전략의 성과가 약해지는데, 이러한 패턴은 팩터 모멘텀과도 연관이 있다.
→ 잘못된 자산가격모형을 사용하여 잔차 모멘텀을 구성할 경우 반영이 되지 않은 팩터에 대한 모멘텀이 잔차 모멘텀에 포함이 되버리는데, 이는 기업에 대한 고유 충격이 IID를 따른다고 해도 발생하게 된다. 따라서 기업 고유 수익률이 모멘텀을 가진다고 말할 수 없으며 실제로 위 그림에서 팩터 모멘텀을 통제할 경우 잔차 모멘텀의 알파도 사라지게 된다.

팩터는 결국 개별 주식의 선형결합으로 이루어진 부산물 아닌가?
→ 앞의 결과를 통해 팩터가 개별 주식과는 구별된다는 것을 시사한다.

추가적으로 본 논문에서는 모멘텀 중립 팩터를 구성한다. 원래 팩터와 최대한 가깝게 유지하면서 과거 주식 수익률과는 직교하도록 만드는 것으로, size의 경우 과거 주식 수익률이 동일한 소형주와 대형주를 롱숏하는 구조이다.
→ 결과적으로 모멘텀 중립 팩터가 기존 팩터보다 더 큰 모멘텀을 보이며 팩터 모멘텀 또한 모멘텀 중립 팩터가 기존 팩터를 흡수하는 것을 보였다.

또한 본 논문에서 고려한 다양한 팩터 모멘텀 전략 중 샤프비율이 가장 높은 전략은 모멘텀 중립 팩터에서 추출한 고유값이 큰 PC 팩터에서의 모멘텀 전략으로, 이 전략의 5팩터 모델에 대한 알파는 t=7.53 으로 유의하게 나타났다.

이러한 결과는 Cochrane(2011) 이 제기한 질문인 “왜 모든 모멘텀 주식들이 다음 달에 함께 상승하고 하락하는가? 마치 하나의 공통 리스크에 노출된 것처럼” 에 대한 답을 제공한다.
모멘텀 주식이 함께 움직이는 이유는 동일한 체계적 위험에 노출되어 있기 때문으로, 수익률이 좋은 주식은 잘나가는 팩터와 양의 상관관계를, 못나가는 팩터와 음의 상관관계를 가지기 때문이다.

이러한 모멘텀이 독립적인 리스크 팩터인지에 대해서는 명확히 짚고 넘어갈 필요가 있는데, FF5 팩터 모델의 5개 팩터의 정적 조합으로는 모멘텀을 설명할 수 없기에 구분되지만, 본 논문에서는 다른 팩터들을 타이밍함으로써 모멘텀 수익을 전부 포착할 수 있음을 보인다.

본 논문의 실증분석에서는 10개의 PC 팩터에서 발견된 모멘텀이 개별 주식 모멘텀의 모든 버전을 포함한다는 것을 보여준다. 그러나 이를 팩터 모멘텀에서 비롯된 것 이외에 주식 수익에서 모멘텀이 존재하지 않는다고 해석할 수는 없다. 보다 신중한 해석은, 팩터 모멘텀이 주식 모멘텀 수익의 상당 부분을 설명한다는 것이다.
→ 팩터 모멘텀을 제외한 순수 주식 수익에도 모멘텀이 존재할 가능성을 배제하지 않음.

2. Autocorrelation in Off-the-Shelf Factors

2.1 Data

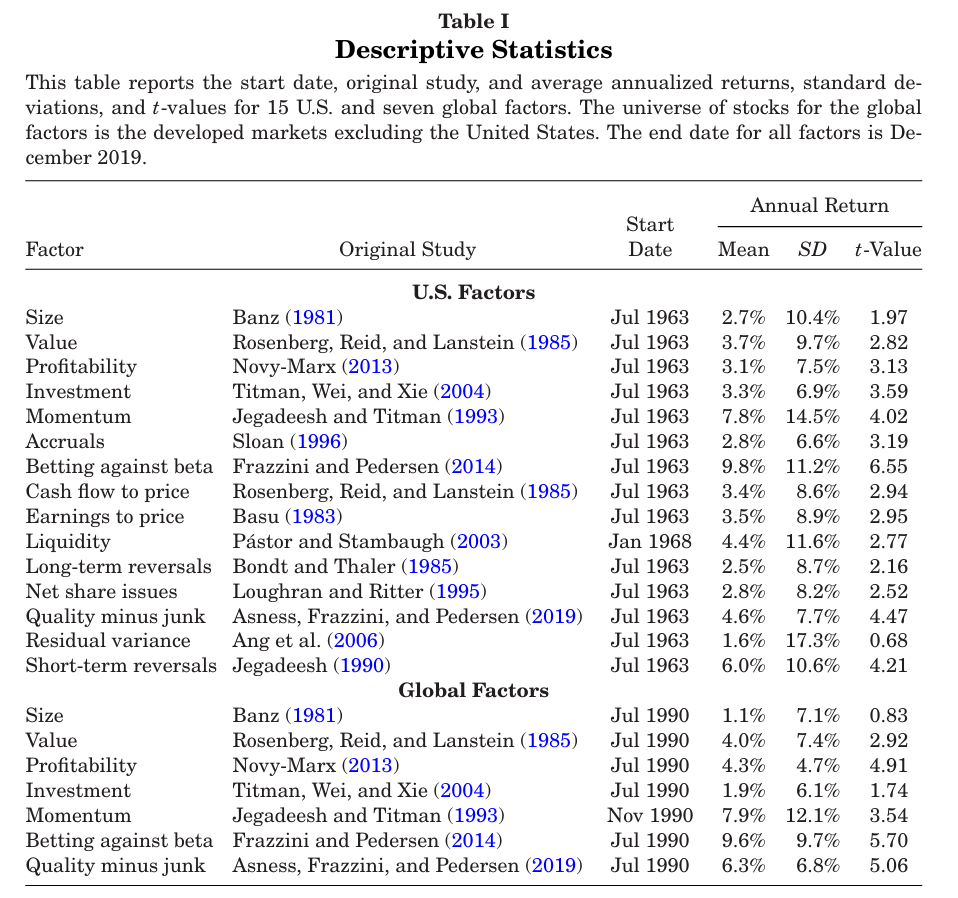
데이터는 Kenneth French, AQR, Robert Stambaugh의 데이터 라이브러리에서 월간 팩터 데이터를 수집한다.
데이터가 제공되지 않을 경우, 팩터 수익률을 상위 3개 decile - 하위 3개 decile로 계산하여 사용한다. 상&하위 decile 정의는 기존 연구에서 사용된 방식을 따른다.

위 표에 존재하는 22개의 팩터를 본 논문에서는 “off-the-shelf” 팩터라고 부른다. 이후 47가지의 미국 팩터로 구성된 더 넓은 집합에 대해 연구한다.

2.2 Factor Returns Conditional on Past Returns

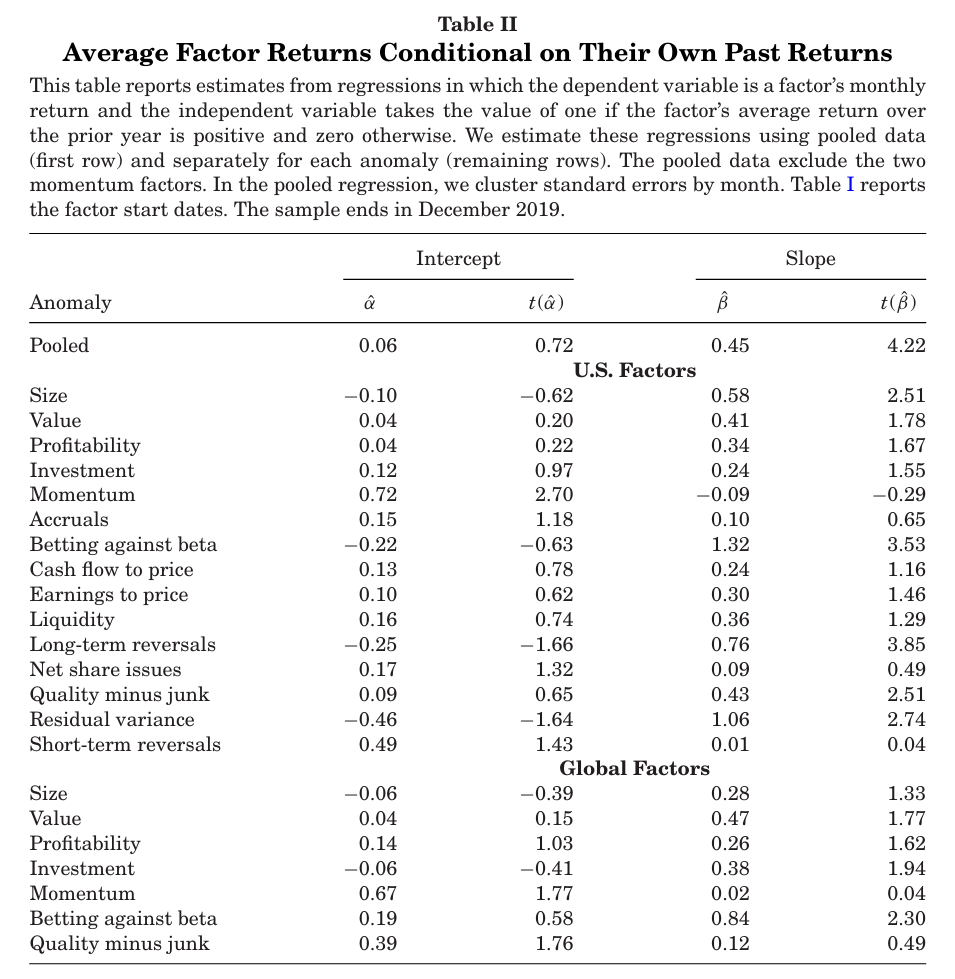
표 2는 팩터들의 과거 수익률이 미래 수익률을 유의미하게 예측함을 보여준다.

• 종속 변수가 팩터의 t월 수익률, 독립변수가 t-12월 부터 t-1월까지의 팩터 성과 지표인 시계열 회귀분석을 진행.
• 팩터 수익률이 양수일 경우 1, 아닐 경우 0의 값을 가짐.

베타값의 경우 US 모멘텀 팩터를 제외한 모든 팩터가 양의 기울기를 가지며, 10개의 팩터가 10% 수준에서 유의하다. 알파의 경우 표1의 결과에서 모든 팩터의 무조건 평균이 양수였음에도 불구하고 6개의 팩터에서 음의 평균 수익률을 가진다.

또한 첫 번째 행인 Pooled는 팩터 프리미엄의 예측 가능성이 경제적 및 통계적으로 큰 수준임을 보여준다.

• 모멘텀 팩터 2개를 제외한 20개 팩터를 대상으로 Pooled regression을 진행한 결과 알파는 6pb(t=0.72)에 불과하며, 기울기는 45bp로 유의한 값을 가진다.

※ Section 1의 Internet Appendix에서는 표2에 나열된 팩터를 거래하는 팩터 모멘텀 전략을 각각 시계열, 횡단면 전략으로 구분하여 분석한다. 결과적으로 연환산 수익률은 시계열 팩터 모멘텀의 경우 3.9%, 횡단면 팩터 모멘텀은 2.4%로 모두 유의했다.
→ 시계열의 경우 팩터 수익률의 자기상관관계에 순수하게 베팅하기 때문에 횡단면 전략보다 더 좋은 성과를 낸다. 전반적으로 여러 팩터들이 동시에 움직이기 때문.

팩터 모멘텀 전략의 특징 중 하나는 투자자들이 평균적으로 어느쪽 구간이 더 높은 수익을 얻는지 미리 지정하지 않고도 모멘텀 프리미엄을 포착할 수 있다는 점이다.
→ ex. AMB 팩터가 있다고 가정하자. 이 팩터가 무조건적 수익률 프리미엄이 존재한다고 믿는 투자자의 경우 A or B 중 어느쪽이 더 성과를 내는지 판단해야 한다. 반면 팩터 수익의 자기상관관계로 이익을 얻고자 하는 투자자는 팩터의 무조건적 수익 평균이 필요하지 않다. 단순히 AMB 팩터가 과거 1년동안 양수 수익률이었으면 매수, 음수 수익률이었으면 매도하면 된다.

이는 표2의 결과에서도 알 수 있는데, 완벽하게 방향을 예측한 투자자도 51bp(45+6)을 얻는 반면, 팩터 모멘텀 투자자도 45bp만큼의 수익을 챙겨갈 수 있음을 보인다.

3. Factor Momentum and the Covariance Structure of Returns

3.1 Factor Momentum in Economies with Sentiment Investors

팩터가 자기상관을 갖는 이유는 무엇인가?
이 질문에 답하기 위해 본 절에서는 KNS를 바탕으로 팩터가 모멘텀을 나타내는 조건을 도출하고, 가장 큰 모멘텀을 나타내는 팩터의 특성을 설명한다.

※ KNS?
경제에는 두 가지 유형의 위험 회피 투자자가 존재하는데,

• 완전히 합리적인 차익거래자 → 진짜 분포를 알고있음.
• 자산 수익률의 실제 분포에 대한 잘못된 믿음을 가진 심리 투자자
  자산 현금흐름은 IDD이며(즉 모멘텀 X), 공분산 행렬은 소수의 지배적인 팩터들로 설명된다.
  심리 투자자의 수요에는 감정에 의해 유발된 추가적인 수요 성분이 존재하며, 높은 레버리지를 사용할 수 없고 공매도도 제한된다. 합리적 차익거래자는 심리 투자자와 반대 방향으로 거래하게 되는데, KNS는 이러한 조건 하에서 심리적 요소가 자산가격을 언제 얼마나 왜곡하는지 분석한다.

KNS의 핵심 발견은 차익거래자들이 공통 팩터 공분산과 일치하지 않는 감정 기반 수요는 거의 완전히 흡수하지만, 공분산과 연결된 심리적 요소는 팩터 리스크를 안아야 하기 때문에 반대 투자를 꺼려하므로 팩터 모멘텀 현상이 일어난다는 것이다.

따라서 KNS의 결론은 근접 차익거래 기회의 부재와 자산 수익률의 공통성이 결합되어 확률적 할인 요인(SDF)을 몇 가지 팩터의 함수로 표현시킬 수 있음을 보장한다는 것이다.
→ 그렇다고 이렇게 만든 가격이 합리적이라고 볼 수는 없음. 팩터에도 왜곡이 남을 수 있기 때문.

여기서부터는 팩터 모델 안에서 어떻게 자산 수익률과 팩터 수익률이 자기상관을 가지고 움직이게 되는지 이론적으로 밝혀본다.
$R_{t+1} = D_{t+1} + a_1 (\xi_{t+1} - \xi_t) - R_f (a_0 + a_1 \xi_t)$

• $R_{t+1}$ 은 자산 수익률의 N by 1 벡터
• $D_{t+1}$ 은 배당금, $R_f$ 는 무위험 이자율, $\xi_t$ 는 투자자 심리 수요
  → 투자자 심리 수요는 AR(1) 과정을 따르며, $\xi_{t+1} = \mu + \phi \xi_t + \nu_{t+1}, \,\text{var}(\nu_{t+1}) = \omega^2$ 가 성립한다.
• 아때 투자자 심리 수요는 $\xi_t$ 크기만큼 $\delta$ 방향으로 왜곡된다.

수익률의 자기공분산 행렬은
$\text{cov}(R_t, R_{t+1}) = a_1 a_1’ \sigma^2 \left[(1+R_f^2)\phi - R_f - R_f \phi^2\right]$

※ $R_{t+1}$ 의 수익률 식에서 상수인 a, D 는 제외하고 공분산을 계산하면 $\text{cov}(R_t,R_{t+1})=\text{cov}(a_1(\xi_t-R_f\xi_{t-1}),a_1(\xi_{t+1}-R_f\xi_t))$
이때 공분산에서 상수계수는 밖으로 빼낼 수 있음.
$\text{cov}(R_t,R_{t+1})=a_1a_1’\text{cov}(\xi_t-R_f\xi_{t-1},\xi_{t+1}-R_f\xi_t)$
위 공분산을 전개하면
$\text{cov}(\xi_t-R_f\xi_{t-1},\xi_{t+1}-R_f\xi_t) =\text{cov}(\xi_t,\xi_{t+1}) -R_f\text{cov}(\xi_t,\xi_t) -R_f\text{cov}(\xi_{t-1},\xi_{t+1}) +R_f^2\text{cov}(\xi_{t-1},\xi_t)$
여기서 AR(1) 성질을 활용하면, 정상성 가정 하에서

• $\text{var}(\xi_t)=\sigma^2=\frac{\omega^2}{1-\phi^2}$
• $\text{cov}(\xi_t,\xi_{t+1})=\phi\sigma^2$
• $\text{cov}(\xi_{t-1},\xi_t)=\phi\sigma^2$
• $\text{cov}(\xi_{t-1},\xi_{t+1})=\phi^2\sigma^2$
  이제 위 공분산 식에 대입하면
  $\text{cov}(R_t, R_{t+1}) = a_1 a_1’ \sigma^2 \left[(1+R_f^2)\phi - R_f - R_f \phi^2\right]$

KNS에 따르면, $a_1$ 을 미정계수법을 사용하여 차익거래자의 1차 조건(FOC, $E_t[R_{t+1}]-\gamma Var_t(R_{t+1}) y_t = 0$ )과 시장 균형 조건($Ny_t+\delta \xi_t=0$)을 결합하여 해결할 수 있다.

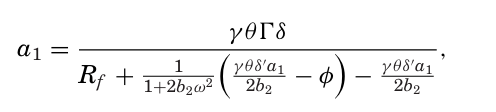
이때 $b_2$ 는 1차 조건에서 $\xi_t$ 에 곱해지는 항에 나타나며, 시장 균형이 $\xi_t$ 의 어떤 값에 대해서도 성립해야 하기 때문에 기울기는 0이어야 한다.

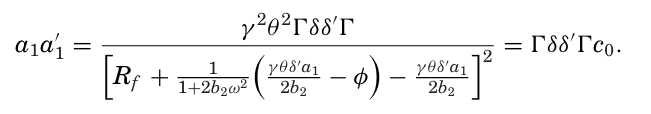
→ (KNS의 논문을 읽어보지 못해서 수식 유도를 완벽히 숙지하지 못했다. 이부분을 이해하기 위해서는 더 많은 공부가 필요할 것 같다…)

KNS에서의 팩터는 자산 현금 흐름의 공분산 행렬의 고유벡터로, $\Gamma = Q \Lambda Q’$ 로 나타난다.
Q는 고유벡터 행렬이고 $\Lambda$ 는 고유값을 가진 대각 행렬이다(이때 Q는 직교행렬이므로 Q’Q = I 성립).
k번째 주성분 팩터 $q_k$ 를 고려하여 자기공분산을 구하면

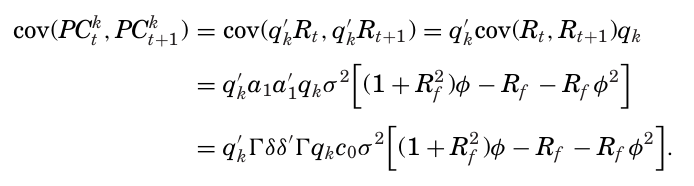
KNS는 δ를 PC들의 선형 결합으로 나타내 δ = Qβ로 표현함으로써 PC와 δ 사이의 연관성을 특징지었다. 이 식과 고유값 분해 식으로 $q’_k \Gamma δδ’ \Gamma q_k$ 를 다음과 같이 나타낼 수 있다.

따라서 따라서 k번째 주성분의 자기공분산은

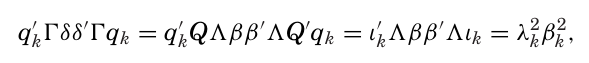
위 식의 대괄호 안 표현은 자기공분산의 부호를 결정한다. 이 표현은 φ에 대한 이차함수로, 오목하며(2차계수 음수) 두 개의 근을 갖는다.
$\phi=\frac{1}{R_f} \quad\text{and}\quad \phi=R_f$

이때 ϕ는 정상성 가정에 의해 절댓값이 1보다 클 수 없고 $R_f$ (무위험 총수익률) 는 1보다 크므로, 대괄호 안의 식이 양수가 되는 구간은 ($\frac{1}{R_f}$, 1]이다.

이는 심리가 유지될 때 팩터 모멘텀 현상이 발생하고 심리 요소에 대해 평균회귀가 이루어질 경우 팩터 리버절 현상이 발생함을 의미한다.
→ 차익거래자는 팩터가 리버절( $φ < \frac{1}{R_f}$ )이나 모멘텀( $φ > \frac{1}{R_f}$ )을 나타낸다는 것을 알긴 하지만, 이러한 패턴을 무효화하는 포지션을 취할 경우 팩터에 대한 리스크를 감수해야 하기 때문에 적극적으로 거래하기를 주저한다. 따라서 팩터 모멘텀이 완전히 상쇄되지 않고 남아있다.

이 모델에서는 감정이 팩터 모멘텀을 생성하기 위해 매우 높은 자기상관을 가져야 한다.
1965년 7월부터 2018년 12월까지 평균 월간 무위험 수익률이 0.39%일 때, 팩터 모멘텀에 대한 임계값은 φ>0.996이다.
→ 이렇게까지 높아야 하는가? 실질적으로 가능한 값인가?
같은 기간동안 Baker and Wurgler(2006) 의 감정 지수의 1차 자기상관 계수가 0.986이고, Dickey and Fuller(1979) 의 단위근 검정이 10% 수준에서 귀무가설을 기각하지 않는다는 것을 통해 φ가 팩터 모멘텀의 임계값을 초과한다는 귀무가설도 기각되지 않는다고 할 수 있다.

또한, KNS모델은 분석의 용이성을 위해 단순화된 모델이기 때문에(현금흐름 IID, 심리의 외생적 영향) 수치적으로 정확하지 않을 수는 있지만 심리의 지속성이 팩터 모멘텀을 만든다는 논리구조는 여전히 성립할 수 있다. 현실 데이터에서도 팩터 수익률이 양의 자기상관을 가지기 때문에 심리 또한 현실 데이터 상에서도 충분히 자기상관적일 것임을 알 수 있다.

그렇다면 KNS 모델에서 어떤 팩터들이 더 큰 모멘텀을 가질까?

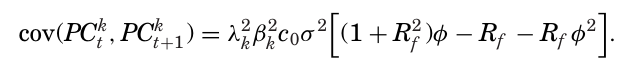
→ 이 방정식에서 $\delta$ 와 일치하는 고유값이 큰 팩터가 더 큰 모멘텀을 가진다는 것을 보여준다.
따라서 해당 결과를 통해 고유값이 큰 팩터들이 모멘텀을 더 잘 나타낸다는 것을 보인다.

3.2 High-Variance PCs and Factor Momentum

이 섹션에서는 Kozak, Nagel, Santosh(2020)의 54개 팩터 데이터를 사용하여 팩터 모멘텀이 고유값이 높은 주성분에 얼마나 집중되는지를 측정한다.
이때 모멘텀과 관련되거나 모멘텀을 다른 특성과 결합한 7개의 팩터는 제외한다.
또한 시가총액이 매우 작거나 유동성이 낮은 주식이 결과에 지나치게 영향을 주지 않도록 분석에서 초소형주는 제외한다.
각 기업 특성 $c_{i,t}$ 에서 i는 기업을 나타내며, 횡단면 순위를 통해 $rc_{i,t} = \frac{rank!\left(c_{i,t}\right)}{n_t + 1}$ 로 나타난다.
이후 정규화를 통해 각 자산의 가중치는 다음과 같이 나타난다.

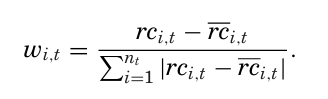
기업 특성값이 누락될 경우에는 가중치를 0으로 설정되며, 팩터 수익률은 $f_t = \sum_{i=1}^{n_t} w_{i,t-1} \, r_{i,t}$ 으로 계산된다.

※ Out-of-Sample 구성 절차

1. 1973년 7월부터 t월까지의 47개 팩터 일일 수익률을 사용하여 상관행렬에서 고유벡터를 계산.
2. PC 팩터 f의 수익률은 $r_{f,t}^{PC} = \sum_{j=1}^{47} v^f_j \, r_{j,t}$ 로, 여기서 $v^f_j$ 는 f번째 고유벡터의 j번째 요소, $r_{j,t}$ 는 개별 팩터 j의 수익률을 의미.
3. 개별 팩터의 분산을 t월까지의 데이터를 사용하여 계산. PC 팩터의 분산이 t월까지의 평균 개별 팩터의 분산과 같고, 평균 수익률이 t월까지 0이 되도록 평균을 제거하고 레버리지를 조정.
4. t-11월부터 t월까지의 평균 수익률이 양수인 팩터는 매수, 음수인 팩터는 매도함으로써 팩터 모멘텀 전략 구축.
5. t+1월에서 팩터 모멘텀 전략의 수익률 계산.

시계열 팩터 모멘텀 또한 모든 팩터의 변동성을 월말까지 동일하게 맞춰 PC 팩터와 비교 가능하도록 조정해준다(3번 과정). 이때 팩터 회전 불안정성(rotation instability)은 모멘텀 신호에 영향을 주지 않는데, 이는 이미 t월에서 고유벡터를 고정했기 때문.

PC를 추출하기 위해서는 최소 10년 이상의 데이터가 필요하므로 팩터 모멘텀 전략의 수익은 1973년 7월부터 시작된다.

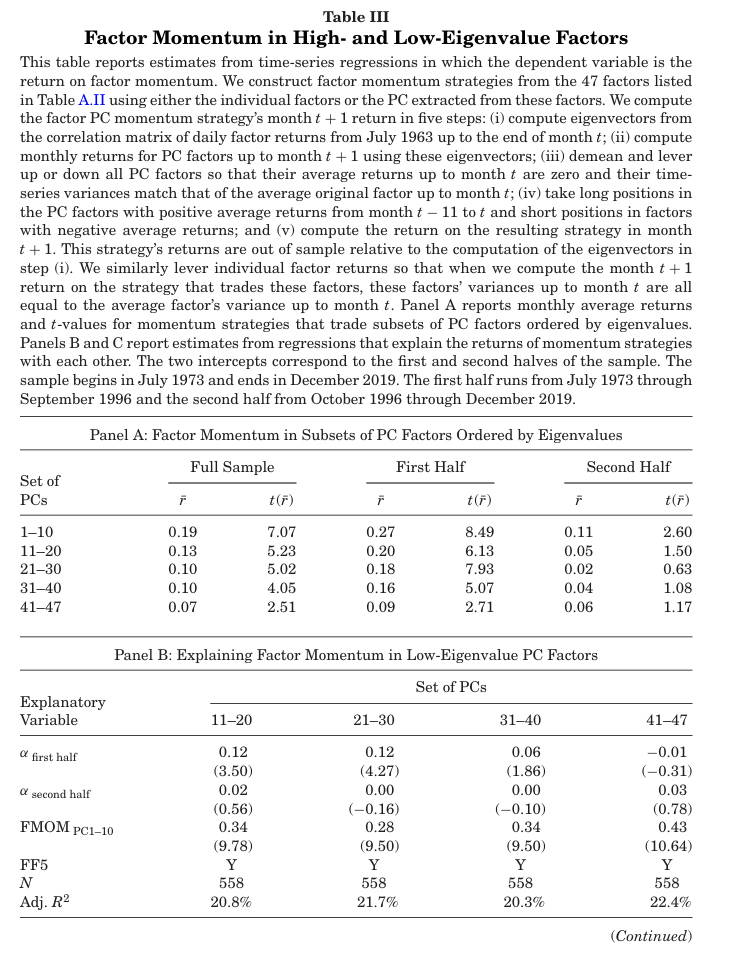
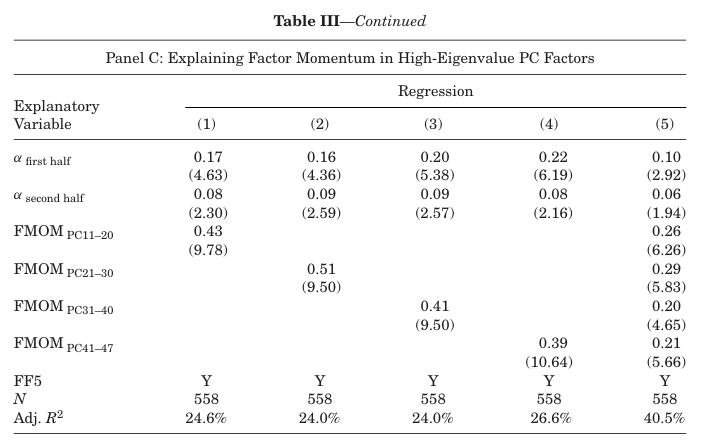
표 3은 47개의 팩터에서 추출한 PC 팩터를 거래하는 팩터 모멘텀 전략의 수익성에 대한 결과를 나타낸다.
예견 편향(lookahead bias)을 피하기 위해 본 연구에서는 t월 말 시점에서 이용 가능한 정보만을 사용하여 PC 팩터의 t+1월 수익률을 계산한다.

• 표 3의 패널 A는 고유값에 따라 정렬된 PC 팩터의 일부를 거래하는 모멘텀 전략의 평균 수익률 및 t-statistics 를 보여준다.
  • 전체 기간동안 PC1-10 에 대한 모멘텀 전략은 매월 19bp의 수익을 가진다(t=7.07).
  • 낮은 고유값의 PC 팩터 모멘텀은 평균 수익률과 t-statistics 값이 더 낮다.
  • 팩터 모멘텀 전략은 샘플 후반부(1996.10~2019.12)에서 수익률 및 t-statistics 값이 더 낮다.
• 패널 B와 C에서는 5가지 팩터 부분집합에서 발견된 모멘텀 수익률이 서로 얼만큼의 상관관계가 존재하는지를 측정한다.
• 패널 B에서는 다음과 같은 회귀분석으로 추정치를 분석한다.
  
  여기서 두 알파는 각 샘플 구간의 PC11-20 팩터 모멘텀 전략의 점진적 수익률을 나타내며, FF5는 Fama-French 5 팩터 모델의 팩터들을 나타낸다.
  → 패널 C에서는 이 회귀를 PC1-10 팩터 모멘텀을 종속변수로, 다른 PC 부분집합 팩터 모멘텀을 설명변수로 하여 진행한다.
• 결과적으로 팩터 모멘텀 전략들은 서로 유의미한 상관관계를 가진다.
  • 기울기 추정치 $\hat b$ 의 t값은 10에 가까운 값을 가진다.
  • 이러한 양의 상관관계는 개별 PC 팩터들은 이론상 서로 직교하기 때문에 놀라운 결과라고 할 수 있음.
    → 이러한 양의 상관관계는 모든 PC 팩터 집합이 동시적으로 모멘텀을 보인다는 것을 나타낸다.
• 패널 B의 first half alpha는 표본의 전반부 동안 PC1-10 팩터 모멘텀이 PC31-40, PC41-47 팩터 모멘텀 전략은 포함하지만 나머지 전략은 포함하지 않음을 보여준다.
• 이는 고유값이 큰 PC 팩터들만으로도 팩터 모멘텀의 기대수익률을 잘 설명할 수 있다고 발견한 KNS와 대조된다.
  → 패널 B의 전반부에 대한 유의미한 알파는 표본의 전반부 동안 모든 모멘텀 수익을 잡기 위해서 더 많은 수의 PC가 필요함을 시사한다.
• 반면 후반부에 대한 알파는 PC1-10 팩터 모멘텀이 다른 모든 전략을 포함한다는 것을 나타낸다.

패널 C는 이러한 스패닝 결과가 양방향으로 작동하지 않음을 보여준다.

• PC1-10 팩터 모멘텀은 다른 모든 팩터 모멘텀을 통제할 때 샘플 전반 및 후반기 수익의 횡단면에 대한 정보 제공 역할을 한다.
  → 이는 고유값이 큰 PC 팩터가 더 많은 모멘텀을 나타낸다는 결과는 모멘텀이 수익의 공분산 구조와 연결되어 있음을 시사한다.
• 인터넷 부록의 Section IV에서도 미국 팩터 14개에 대한 분석 결과 또한 횡단면 변동성을 더 잘 설명하는 특성에 기반한 팩터들(Size, Market Beta, Idiosyncratic Volatility, QMJ 등)이 더 많은 모멘텀을 나타냈다.

샘플 구간에 따른 알파값 차이는 차익거래 활동과 관련이 있는데, 차익거래자들은 시간이 지나면서 모멘텀에 대해 더 많이 알게 될 것이다. 상위 몇 개의 PC 만으로 SDF를 특징짓는 것이 충분하다는 결과는 근사 차익거래 기회가 없다는 가정에 의존하게 되는데, 차익거래자들이 모멘텀에 대해 더 알게되면서 시간이 지날수록 샘플 후반에 알파가 감소하게 되는 것이라고 추측할 수 있다.

4. Factor Momentum and Individual Stock Momentum

4.1 Transmission of Factor Momentum into the Cross Section of Stock Returns

주식 수익률이 팩터 구조를 따른다면, 팩터 모멘텀은 주식 모멘텀의 형태로 나타난다.
자산 초과 수익률이 F-factor 구조를 따르는 팩터 모델을 고려해보자.
$R_{i,t} = \sum^F_{f=1} \beta^f_i r^f_t + \epsilon_{i,t}$
자산 가격이 위 방정식에 따라 변한다고 가정하고, 횡단면 모멘텀 전략을 시행할 때 주식 i에 대한 포지션의 기대 수익은 다음과 같다.
$E [ \pi_{i,t}^{mom} ] = E [ (R_{i,-t}-\bar R_{-t})(R_{i,t}-\bar R_t) ]$
이는 공분산으로 변환해주면,

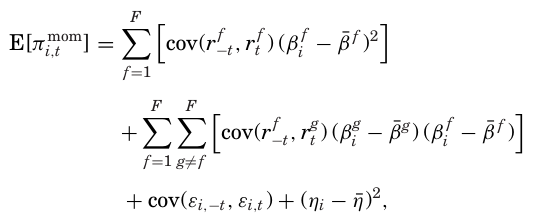
이를 양변에 N을 나눠줌으로써 횡단면 모멘텀 전략의 기대수익률을 구하면,

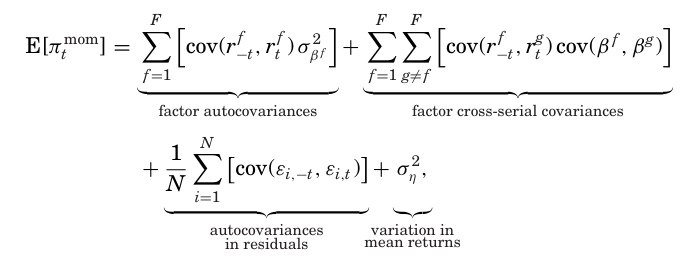
이 식은 횡단면 주식 모멘텀 전략의 수익이 4가지로부터 생성된다는 것을 보여준다.

1. 팩터 수익의 자기상관성이 양수이면 모멘텀 수익이 발생한다(첫 번째 항). 베타의 횡단면 분산은 이러한 효과를 증폭시킨다. 모멘텀의 크기는 팩터의 개수 및 얼마나 자기상관을 가지는지에 달려있다.
2. 팩터 간 수익의 lead-lag 관계가 모멘텀 수익에 기여할 수 있다. 이러한 효과의 크기는 팩터 수익 간의 교차 시차 공분산과 팩터 노출도 간 공분산에 모두 영향을 받는다.
   → 그러나 이 조건은 다소 제한적인데, 이는 팩터 수익의 교차 시차 공분산과 베타 간 공분산의 부호가 같아야 하기 때문.
3. 팩터로 설명되지 않는 개별 기업만의 고유 수익의 자기상관 또한 횡단면 모멘텀의 수익을 증가시킬 수 있다.
4. 개별 종목 평균수익의 횡단면 분산 또한 모멘텀 수익에 기여한다.

4.2 Pricing Momentum-Sorted Portfolios with Equity Momentum and Factor Momentum

이 섹션에서는 팩터 모멘텀이 횡단면 모멘텀 전략의 수익률에 기여하는지에 대해 분석한다.

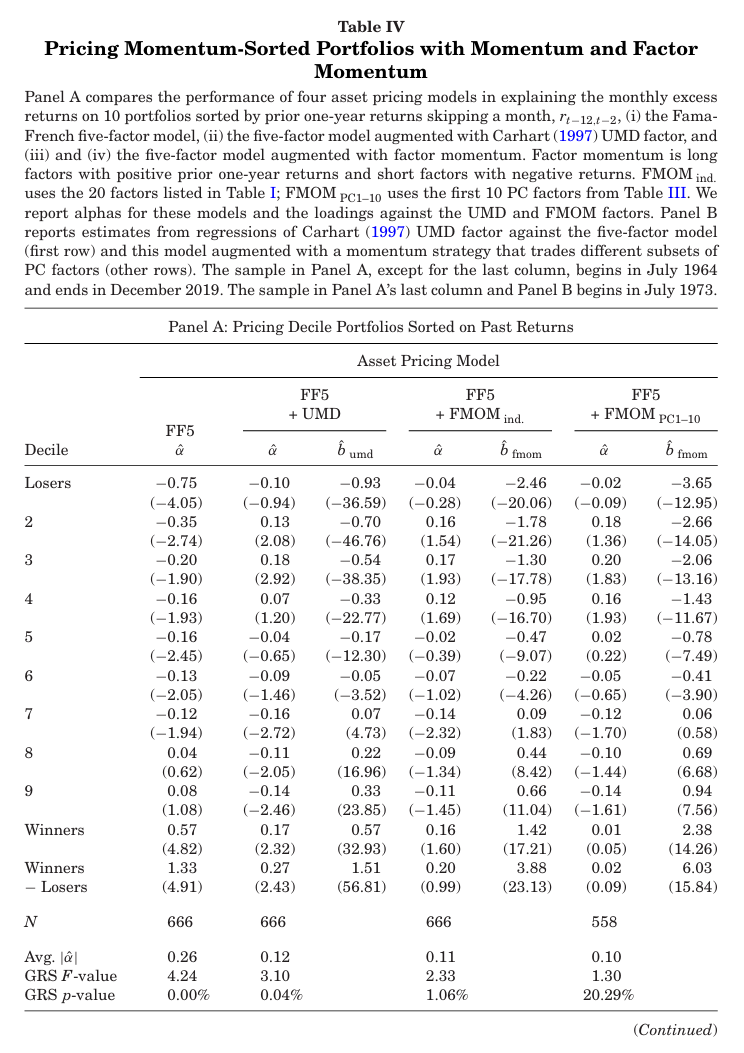
표 4에서는 개별 주식과 팩터 모멘텀 간의 연결성을 보인다. 십분위수에 대한 알파 및 베타(팩터 로딩) 값을 보고한다.

• 패널 A에서는 과거 1년 수익률을 기준으로 직전 한달을 건더뛴 포트폴리오를 가격 책정할 때 4가지 팩터 모델에 대한 성과를 비교한다.
  • 주식 모멘텀은 FF5 팩터 모델의 알파에서 명확히 나타난다. Losers와 Winners의 알파는 각각 -0.75%(t=-4.05), 0.57%(t=4.82)이며, 10분위수에 대한 평균 알파의 절댓값은 26bp이다.
  • FF5+UMD 에 대한 알파의 경우 평균은 12bp로 감소하며, 롱숏 포트폴리오의 수익률 또한 1.33%에서 0.27%로 떨어진다. 하지만 여전히 t-statistics는 2.43으로 유의하다.
  • 20개의 개별 팩터로 구성된 팩터 모멘텀을 추가한 FF5+FMOM(ind)에 대한 알파의 절댓값은 평균 11bp로 떨어지며 GRS 검정 통계량 또한 3.10에서 2.33으로 하락, 롱숏 포트폴리오 수익은 0.27%에서 0.2%로 감소한다.
  • PC1-10 팩터 모멘텀을 추가한 FF5+FMOM(PC1-10)에 대한 알파의 절댓값은 9bp이며 GRS 검정 결과 10개의 테스트 포트폴리오 전체 알파가 0이라는 귀무가설을 기각하지 못한다.
  • 베타값의 경우 모든 모델에서 10분위수에 대해 순서대로 값이 커지는 것을 확인할 수 있다.
    → 결과에서 FF5+FMOM 버전이 FF5+UMD 보다 더 잘 설명된다는 것은 매우 놀라운 일인데, 실질적으로 주식 모멘텀을 나타내는 UMD 팩터가 포함된 것보다 팩터 모멘텀을 포함시킨 모델이 주식 모멘텀을 더 잘 설명하기 때문. 이는 팩터 모멘텀만으로도 주식 모멘텀을 대부분 설명할 수 있다는 것을 나타낸다.
• 표 4의 패널 B는 UMD 팩터를 종속변수로 한 시계열 회귀 추정치를 나타낸다. 첫 번째 행의 모델인 FF5 팩터 모델을 기준으로 각각 PC 팩터 부분집합을 추가 독립변수로 설정해주었다.
  • 높은 고유값을 가지는 PC에 대한 팩터 모멘텀일수록 UMD 수익을 잘 설명하는데, PC1-10 팩터 모멘텀의 경우 UMD의 알파는 -9bp(t=-0.59)인 반면 PC41-47 팩터 모멘텀의 경우 알파는 40bp(t=2.33)이다.
  • 높은 고유값을 가지는 PC에 대한 팩터 모멘텀(PC1-10)은 42.5%의 $R^2$ 값을 가진다.

4.3 Alternative Momentum Factors: Spanning Tests

여기서는 Jegadeesh and Titman(1993) 의 표준 개별 주식 모멘텀 이외에도 UMD 방법론을 사용하여 세가지 다른 모멘텀 팩터를 구성하는데,

1. Cohen and Polk(1998)의 산업 조정 모멘텀(industry-adjusted momentum)
   • 주식을 산업 조정 수익률에 따라 분류
2. Novy-Marx(2012) 의 중간 모멘텀(mediate momentum)
   • t-12월 부터 t-7월 까지의 수익률에 따라 주식 분류
3. Rachev et al.,(2007) 의 샤프비율 모멘텀(Sharpe ratio momentum)
   • 수익률의 변동성으로 조정된 수익률에 따라 주식을 분류
   • 추가적으로 Moskowitz and Grinblatt(1999) 의 산업 모멘텀 전략도 구성(t-6월 수익률 기준으로 20개 산업 분류 후 상위 및 하위 3개 산업에 롱숏).

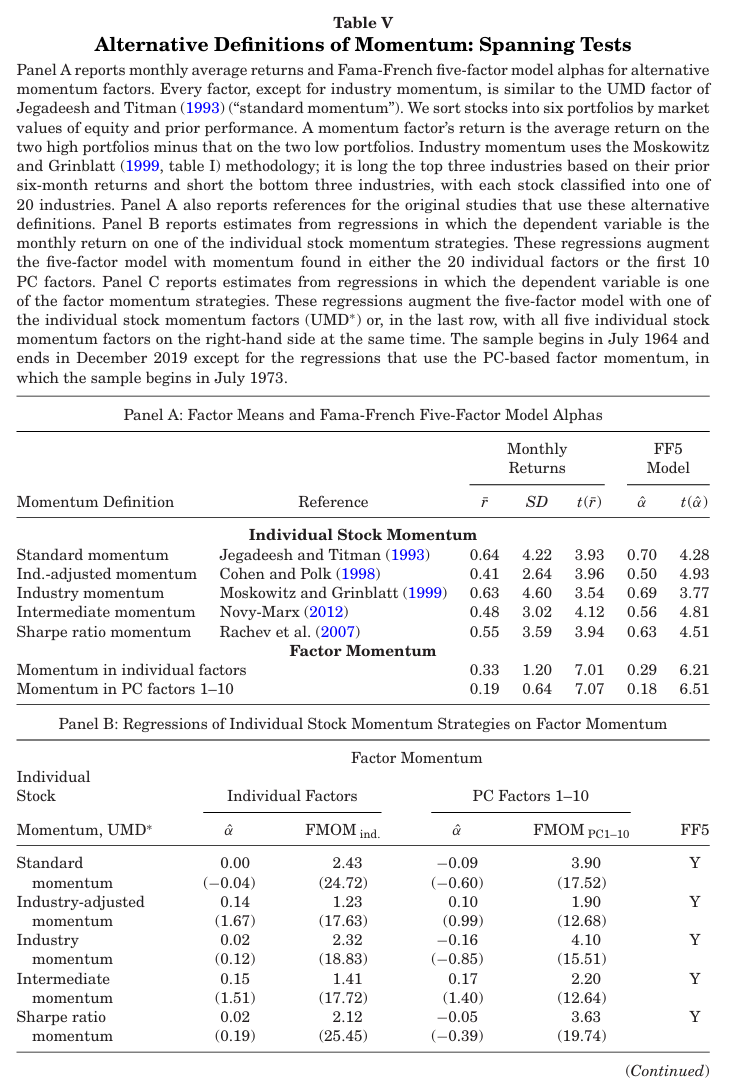
표 5에서는 팩터 모멘텀이 다른 횡단면 모멘텀 전략을 포함한다는 것을 보여준다.

• 패널 A에서는 두개의 팩터 모멘텀 전략(20개 팩터 모멘텀, PC1-10 팩터 모멘텀)과 함께 위에서 구성한 대체 모멘텀 팩터들을 소개한다.
  • 모든 모멘텀 팩터는 통계적으로 유의한 월평균 수익률 및 FF5 팩터 모델에 대한 알파를 보여준다.
  • 두개의 팩터 모멘텀 전략은 가장 낮은 평균 수익률을 보이지만 그만큼 변동성도 가장 낮다.
  • 월평균 수익률 및 FF5 팩터 모델에 대한 알파의 t-statistics 또한 팩터 모멘텀이 가장 크게 나타난다.
    → 월평균 수익률에 대한 t-statistics는 샤프비율, 팩터 모델에 대한 알파의 t-statistics는 정보비율과 비례하기 때문에 위 결과는 팩터 모멘텀의 샤프비율, 정보비율이 가장 높다는 것을 의미함.
• 패널 B는 종속변수를 위에서 구성한 대체 주식 모멘텀 팩터이며 FF5 팩터 모델에 각 팩터 모멘텀 전략을 추가로 독립변수로 넣어준 모델에 대한 회귀분석이다.
• 이 분석은 두 가지의 해석이 존재하는데,
  1. 투자 관점에서 통계적으로 유의한 알파: 투자자가 독립변수로 설정한 팩터 뿐만 아니라 종속변수로 설정한 팩터를 거래한다면 더 높은 샤프비율을 얻었을 것임을 의미.
  2. Asset Pricing 관점에서 통계적으로 유의한 알파: 독립변수 팩터만을 포함한 자산 가격 모델이 종속변수 팩터도 포함하는 모델에 의해 대체된다는 것을 의미.
  • 결과적으로, 패널 A에서 볼 수 있듯 모든 모멘텀 팩터가 통계적으로 유의한 평균 수익 및 FF5 모델에 대한 알파를 보였음에도 불구하고, 두개의 팩터 모멘텀에 의해 알파가 사라지는 것을 확인할 수 있다.

• 패널 C는 개별 모멘텀 팩터들이 사실상 어떤 팩터 모멘텀 전략도 포함하지 못한다는 것을 보여준다.
  • 12번의 회귀 결과에서 팩터 모멘텀의 알파의 t값이 가장 낮은 것은 4.07이다.
  • 마지막 행(All of above)은 FF5 팩터 모델에 주식 모멘텀 팩터들을 전부 추가한 경우로, 이또한 두 팩터 모멘텀 전략의 알파가 유의하게 나타났다(각 t=4.30, 5.45).

따라서 표 5는 팩터 모멘텀이 다른 어떤 형태의 모멘텀 전략에서도 나타나지 않는 정보를 포함하며, 동시에 다른 어떤 형태의 모멘텀도 팩터 모멘텀을 통제했을 때 주식 수익률의 횡단면에 대해 전혀 도움이 되지 않는다는 사실을 보여준다.

4.4 Individual Stock Momentum versus Factor Momentum with Alternative Sets of Factors

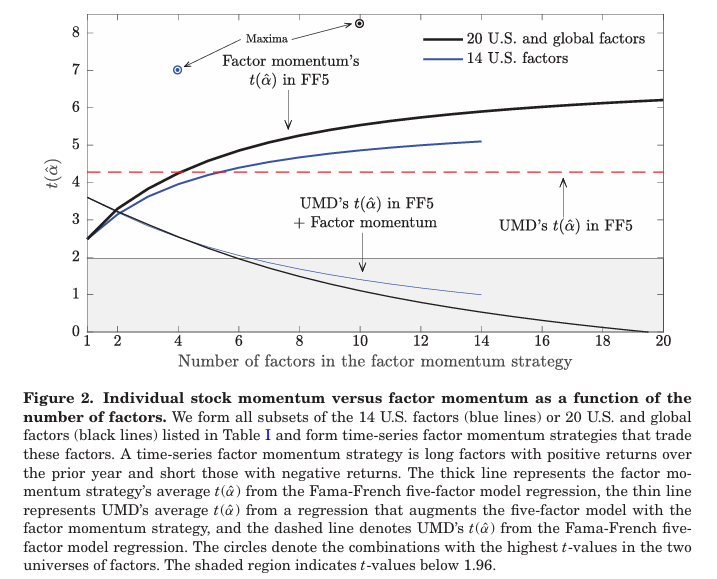
그림 2에서는 20개의 개별 팩터를 거래하는 팩터 모멘텀 전략에 포함된 팩터의 수와 종류에 대한 결과의 민감도를 보여준다.

• 팩터 모멘텀의 5팩터 모델 알파에 대한 t값이 팩터 수에 따라 단조 증가하는 것을 보여준다. 팩터 모멘텀이 단 하나의 팩터에서 거래를 할 경우의 t값은 2.49인 반면, 10개의 팩터를 거래할 때는 5.54, 20개의 팩터를 거래할 때는 6.21이 된다.
• UMD를 포함하는 능력 또한 팩터 수가 증가할수록 향상되는데, 팩터 하나에 대한 팩터 모멘텀 전략은 UMD의 알파가 t=3.60 으로 유의하게 남아있는 반면 10개로 증가할 경우 t=1.10, 20개의 경우 t=-0.04로 알파의 유의성이 사라진다.
• 14개의 US 팩터로 진행해도 패턴은 유사하게 나타난다.

이러한 결과는 팩터 모멘텀이 UMD를 포함하는 능력이 사용된 팩터 집합에 국한되지 않는다는 것을 시사한다.
팩터의 수가 증가하면 대부분의 팩터 집합에서 발견되는 자기상관이 합쳐져 개별 주식 모멘텀을 설명한다. 이는 개별 주식 모멘텀이 팩터 수익에서 발견되는 자기상관의 집합이라는 본 논문의 예측을 뒷받침한다고 할 수 있다.

4.5 Do Firm-Specific Returns Display Momentum?

4.5.1 Simulation Evidence

만약 팩터 모멘텀이 주식 수익률의 횡단면에서 모든 모멘텀을 주도한다면, 개별 기업의 수익률(firm-specific returns)은 어떤 지속성도 나타나지 않아야 한다.
→ 이를 검증하기 위해 본 논문에서는 개별 기업 수익률에서 모멘텀을 측정한다.

그러나 이러한 수익률을 팩터 모델에서 잔차로 추정해야 할 경우 세 가지 문제에 직면하게 되는데,

1. 모든 팩터의 정체를 다 알 수 없음.
2. 실제 팩터 수익률을 관찰할 수 없음(포트폴리오로 근사한 수익률만 있을뿐).
3. 주식의 팩터 로딩을 오차 없이 알 수 없음. 즉 추정치에는 오차가 무조건 존재함.

따라서 진정한 firm-specific returns를 식별할 수 있는 자연 실험이 없는 한, 횡단면 모멘텀을 팩터 모멘텀과 잔차 모멘텀으로 결정적으로 구분하는 것은 불가능하다.
→ 모델에 포함되지 못한 팩터로 인해 발생하는 문제를 설명하기 위해, 두 가지 systematic factor가 초과 주식 수익률을 주도한다고 가정하자.
$R_{i,t} = \beta_{i,1} F_{1,t} + \beta_{i,2} F_{2,t} + \varepsilon_{i,t}$
첫 번째 팩터에 대해서만 아는 연구자는 잔차를 다음과 같이 추정한다.
$\hat\varepsilon_{i,t} = r_{i,t} - \beta_{i,1} F_{1,t}- \beta_{i,2} F_{2,t}$
연구자가 실제 팩터 $F_1$ 과 이에 대한 주식 i의 베타를 관찰한다고 가정하자.
추정된 잔차는 개별 기업 수익이 IID일지라도(즉 모멘텀이 없음) 모멘텀이 나타나버릴 수 있다.

위 식에서, 생략된 팩터 $F_2$ 가 모멘텀을 나타낸다면, $\hat{\varepsilon}_{i,t}$ 도 모멘텀을 나타낼 것이다. 연구자가 기업 고유의 잔차로 보는 것은 알려진 팩터를 뺀 순수 잔차에 불과하며, 진짜 팩터나 베타를 관찰하지 못할 경우 생략된 팩터 모멘텀 문제는 더욱 심각해질 것.

아래 실험에서는 팩터 모멘텀과 잔차 모멘텀의 분리 어려움을 보인다.
오직 팩터 수익률만 양의 자기상관을 가지는 경제상황을 가정하여 수익률을 시뮬레이션한다. 주식 수익률은 10개의 systematic factor와 IID인 firm-specific으로 이루어진다.
팩터의 위험 프리미엄은 AR(1) 과정을 따르며 팩터 수익률은 이 위험 프리미엄과 기업 고유 충격의 합으로 구성된다.

본 논문에서는 두 가지 팩터 가정 하에서 데이터를 시뮬레이션한다.

1. Sysmmetric factors
   • 10개 팩터의 분산이 모두 동일
   • 모든 팩터 위험 프리미엄의 지속성도 동일
2. Uncorrelated market factor
   • 첫 번째 팩터가 다른 9개 팩터보다 횡단면 수익을 5배 더 많이 설명
   • 하지만 이 첫 번째 팩터의 위험 프리미엄은 자기상관 X
     → 즉 첫 번째 팩터를 시장 팩터로 설정

시뮬레이션에서 평균 비시장 팩터의 자기상관은 실제 데이터와 유사하다.
→ 실제 데이터에서 t월 수익과 t-12~t-1 월 평균 수익 상관은 0.25, 시뮬레이션은 0.2

이러한 시뮬레이션 수익률을 사용하여 세 가지 모멘텀 전략을 구성한다.

1. 개별 주식 모멘텀 전략
   • 지난 1년 동안 수익률이 가장 높은 상위 10% 주식 매수, 하위 10% 주식 매도
2. 잔차 모멘텀 전략
   • 지난 1년 동안 firm-specific 수익률 기준으로 상하위 10% 롱숏
   • t-72~t-13월 까지의 각 팩터만큼 사용한 모델에서 추정한 베타값으로 t-12~t-1월 까지의 잔차 계산
3. 팩터 모멘텀 전략
   • 지난 1년 동안 수익률이 양수인 팩터 매수, 음수인 팩터 매도

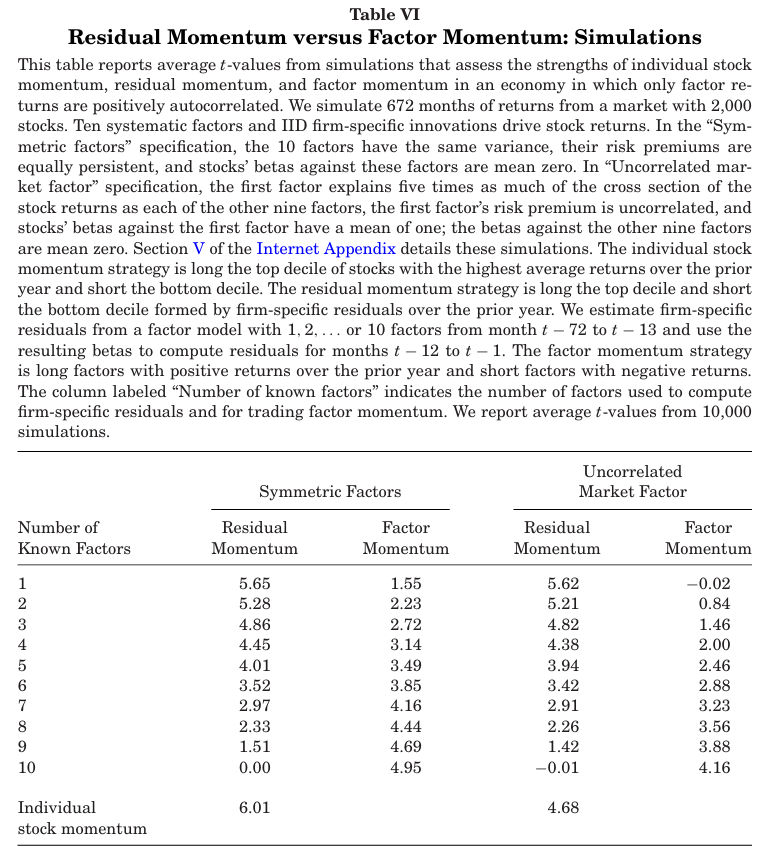
표 6은 위 시뮬레이션 구성에 맞게 10,000번 진행하여 얻은 t-statistics를 나타낸다.

• Sysmmetric factors 에서 개별 주식 모멘텀 전략은 t=6.01로 유의하며, 이는 팩터 위험 프리미엄의 지속성에 간접적으로 베팅하기 때문에 수익성이 생기는 것이다.
• 잔차 모멘텀 전략은 팩터를 2개 생략하는 것 까지 유의한 수익을 가진다. 이때 t값은 2.33이다.
• 모든 팩터를 모델에 넣을 경우 잔차는 기업의 고유 충격과 같아지며 이때의 잔차 모멘텀은 수익이 나지 않는다.

• 팩터 모멘텀 전략은 팩터가 양의 자기상관을 가지기에 수익이 생기며, 팩터 수가 많아질수록 수익이 더 유의하게 나타난다.

• Uncorrelated market factor 에서는 첫 번째 팩터만 사용하는 모델에 대한 잔차 모멘텀의 t=5.62인 반면 개별 주식 모멘텀은 t=4.68로 잔차 모멘텀이 더 강한 것을 알 수 있는데, 이는 자기상관이 존재하는 9개의 팩터가 잔차로 들어가버리면서 잔차 모멘텀이 생기기 때문이다.
• 팩터를 모델에 추가할수록 잔차 모멘텀의 수익이 감소하지만 최대 3개의 팩터까지는 개별 주식 모멘텀보다 높은 수익을 가진다.
• 팩터를 추가할수록 팩터 모멘텀의 수익은 높아지지만 시장 팩터를 추가하면 손해를 본다.

따라서 표 6에서는 자산 가격 모델이 불완전할 경우 잔차 모멘텀 전략은 누락된 팩터로 인한 모멘텀에서 수익이 발생하기 때문에 팩터 모멘텀과 잔차 모멘텀을 분리하는 것이 어렵다는 것을 보여준다.

4.5.2 Actual data

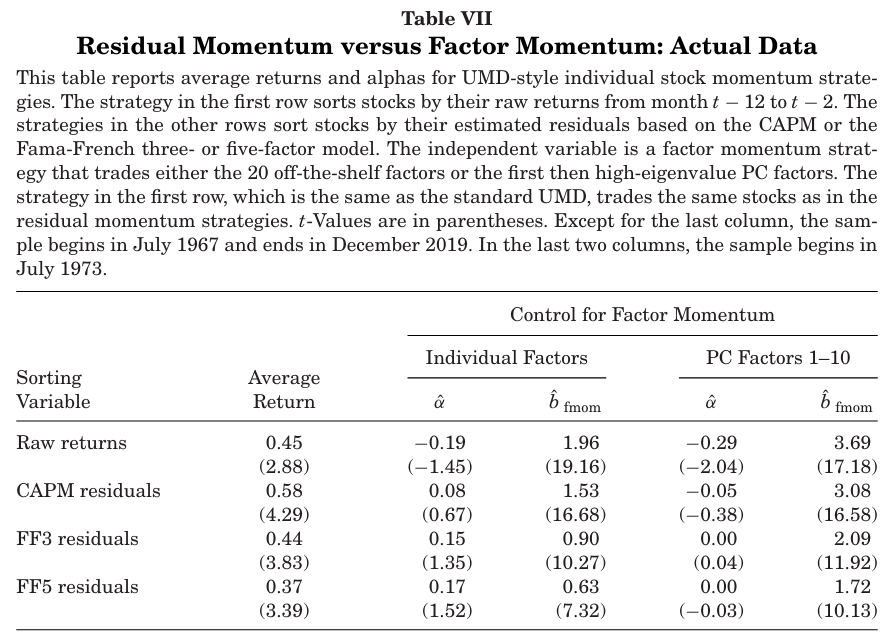
표 7에서는 세가지 잔차 모멘텀 전략의 수익성을 살펴본다(CAPM, FF3, FF5).
t-72~t-13월 까지의 데이터를 사용하며 이렇게 추정된 베타값으로 t-12~t-2월의 평균 잔차를 계산한다. 이후 주식을 시가총액과 과거 수익률에 따라 6개의 포트폴리오로 나누고 상하위 포트폴리오에 롱숏하여 UMD와 유사한 형태로 구성한다.

• 비교를 위해 같은 자산군으로 UMD 팩터 재계산

• 개별 주식 모멘텀 전략은 월평균 45bp(t=2.88)의 수익을 보인다. 알파값은 팩터 모멘텀 전략 중 하나를 통제하면 음수로 전환된다.
• CAPM 잔차 모멘텀은 58bp(t=4.29)로 주식 모멘텀 전략보다 수익성이 더 높다.
  → 이 결과는 시장 팩터가 수익률의 횡단면 변동성을 설명하는 정도에 비해 자기상관이 약하다는 견해와 일치하며, 이 팩터를 제거하면 잔차가 다른 팩터들에 대해 더 많은 정보를 제공한다.
• CAPM 잔차 모멘텀은 두개의 팩터 모멘텀 전략과도 유의하게 상관된다. 20개 팩터 모멘텀 전략을 통제할 경우 알파는 8bp(t=0.67), PC1-10 팩터 모멘텀을 통제할 경우 -5bp(t=-0.38)의 수익을 가진다.
• FF3 잔차 모멘텀은 CAPM 잔차 모멘텀보다 수익성이 낮다(44bp, t=3.83).
• FF5 잔차 모멘텀은 수익성이 낮은데(37bp, t=3.39), 이는 추가적으로 통제되는 팩터들이 모멘텀 수익에 의미있게 기여했기 때문임을 시사한다.
• 위에서 구성한 3개의 잔차 모멘텀 전략 모두 팩터 모멘텀을 통제하면 알파는 0에 가깝다.

표 7의 결과는 개별 주식 수익률의 모멘텀이 팩터에서 비롯되어 증가한다는 것과 일치한다.
매우 체계적인 팩터가 자기상관은 낮을 때 해당 팩터를 제거하면 모멘텀 수익이 높아지지만, 모멘텀 수익에 기여하는 팩터가 제거될 경우 잔차 모멘텀의 수익은 감소한다.

즉, “잔차가 팩터 모멘텀을 제외한 기업의 고유 모멘텀을 얼마나 나타내는가?”는 잔차를 추정할 때 사용된 팩터 모델에 들어가지 않은 팩터의 특성에 따라 달라진다. 또한 FF5 팩터 모델에 없는 추가 팩터가 무엇이던간에, 잔차 모멘텀은 PC-10 팩터 모멘텀으로부터 포함된다.

인터넷 부록의 Section III에서는 선형 가중치 분해(linear weight decomposition)를 다시 살펴보고, 팩터 모멘텀, 잔차 모멘텀, 누락된 팩터 모멘텀 사이의 긴장 관계에 대해 동일한 결론에 도달한다.

CAPM 하에서는 이 분해가 수익의 거의 대부분을 기업고유 수익의 자기상관으로 귀속시키는 반면, 7팩터 모델에서는 수익의 대부분을 팩터 수익의 자기상관에 귀속시킨다. → omitted-factor tension

또한 잔차 모멘텀 전략은 기업 고유 수익에 대한 모멘텀 뿐만 아니라 베타에 대한 반대 포지션으로 인해 수익성이 생긴다. → 기업의 추정 잔차 수익 = 해당 기업의 수익 - 추정된 팩터 로딩 * 팩터 수익
→ 즉 잔차가 높은 기업은 수익이 높거나 추정 베타가 낮은 경우이므로, 잔차 모멘텀은 간접적으로 저베타 주식을 매수 & 고베타 주식을 매도하는 전략

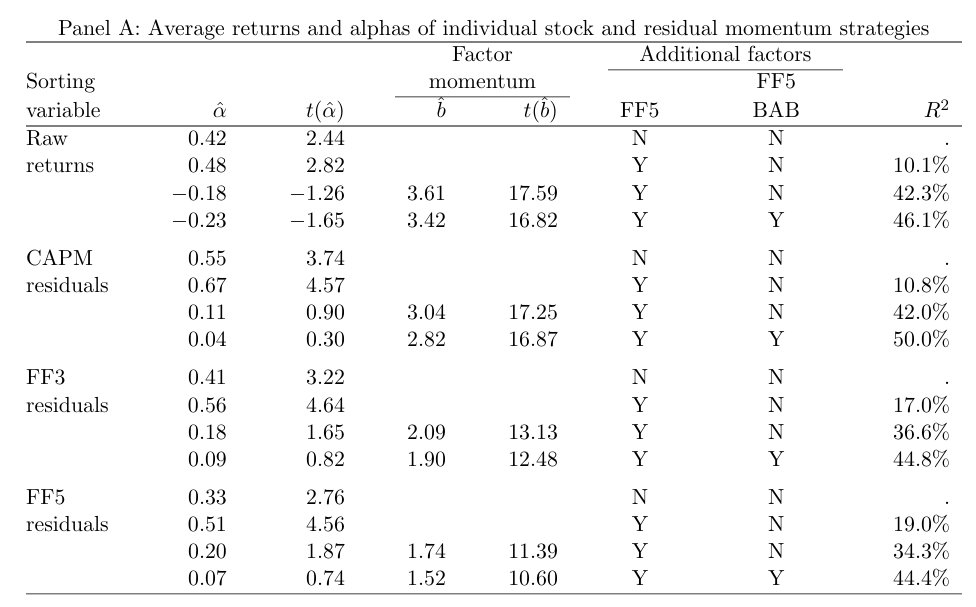
인터넷 부록 Section VI에서는 잔차 모멘텀 전략이 실제로 유의미하게 베타에 대해 반대 베팅을 하고 있음을 보인다. 이 전략의 5팩터 모델 알파가 평균 수익보다 큰 이유는 이러한 베타 반대 베팅 때문이며 베타에 대한 반대 베팅 팩터를 통제하면 팩터 모멘텀 전략이 세가지 잔차 모멘텀 전략을 포괄한다.

5. Momentum vis-à-vis Other Factors

5.1 Unconditional and Conditional Correlations with the Momentum Factor

개별 주식 모멘텀의 가장 신기한 점은 다른 팩터들과 상관관계가 낮다는 것이다.
1963년 7월부터 2019년 12월까지 UMD를 FF5 팩터 모델에 회귀한 adjusted $R^2$ 는 고작 9%에 불과하다.
그러나 UMD와 다른 팩터들 간의 무조건적 상관관계는 이들 간의 연관성을 과소평가한다.
ex. Size 팩터를 고려해보자. Size 팩터가 좋은 성과를 냈다면 UMD는 소형주에 롱, 대형주에 숏을 취했을 것. 그러면 UMD와 SMB 모두 소형주에 롱, 대형주에 숏을 치게 되므로 다음 달에는 두 팩터가 양의 상관관계를 가질 것이다. 반대의 경우는 두 팩터가 음의 상관관계를 가질것.

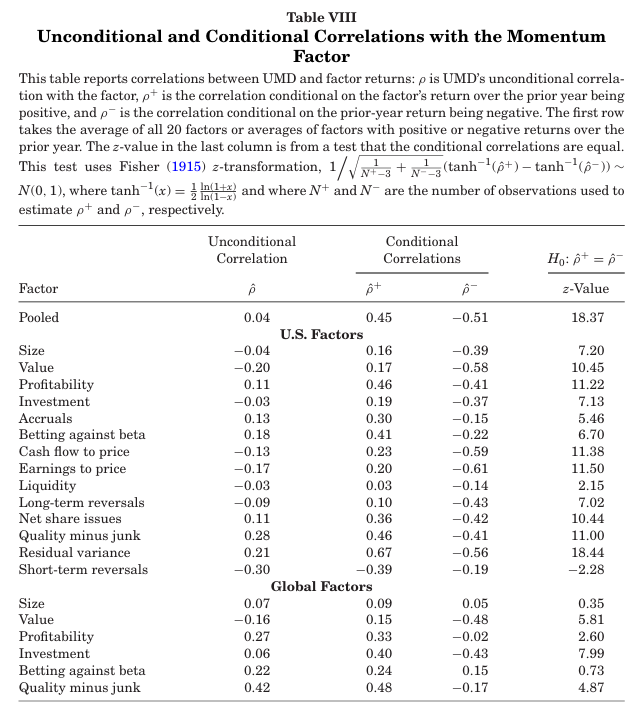
표 8에서는 팩터들과 UMD의 상관관계를 나타낸다.
여기서는 세 가지의 상관관계를 보이는데,

1. 무조건적 상관관계(unconditional correlation)
2. 전년도 팩터 수익률이 양수일 때 조건부 상관관계
3. 전년도 팩터 수익률이 음수일 때 조건부 상관관계

• UMD와 팩터들 간의 무조건적 상관관계는 낮다. 팩터 20개중 11개가 양수이며, 20개 팩터 전체 포트폴리오(Pooled)와의 상관관계는 0.04이다.
• 전년도 팩터 수익률이 양수일 때의 조건부 상관관계는 단기 반전 팩터(Short-term reversals)를 제외하고 모든 팩터에서 무조건적 상관관계보다 높았으며, 19개 팩터중 17개 팩터에서 5% 유의수준에 통계적으로 유의했다.
• Pooled의 경우 각각 0.45, -0.51의 상관관계를 가지며 통계적으로 유의하다.

모멘텀과 다른 팩터들 간의 무조건적 상관관계가 0에 가깝기 때문에 5팩터 모델과 같은 대부분의 팩터 모델들은 모멘텀 수익을 설명하지 못한다.
→ 그러나 이 결과가 “모멘텀이 다른 팩터들과 무관하다.” 를 의미하진 않음.

표 8은 이러한 무조건적 상관관계가 0에 가까운 이유는 이 상관관계가 시간에 따라 유의미하게 변하기 때문임을 보여준다. 따라서 실제로 모멘텀 팩터(UMD)는 다른 팩터들과 관련이 있다고 할 수 있다.

5.2 Momentum in Momentum-Neutral Factors

모멘텀은 팩터에 존재하는가, 아니면 개별 주식에 존재하는가?
이러한 인과관계를 보여주는 데 있어 모호한 부분은, 개별 주식 모멘텀이 우연히 팩터 수익률에 모멘텀을 유발할 수 있다는 것이다.
ex. Size팩터가 지난 1년 동안 좋은 성과를 보였다면, 이 팩터의 롱 대상(소형주)은 정의상 숏 대상 집단(대형주)보다 과거 수익률이 더 높다. 개별 주식 모멘텀이 존재한다면, 과거에 수익이 좋았던 주식인 소형주를 매수, 수익이 좋지 않았던 대형주를 매도하기 때문에 Size 팩터 또한 좋은 성과를 낼 것.
→ 이러한 우연적인 모멘텀 효과는 모멘텀이 실제로 팩터에 존재하지 않더라도 팩터 모멘텀이 있는 것처럼 보이게 할 수 있다.

따라서 이 섹션에서는 이러한 메커니즘이 팩터 모멘텀 수익에 얼마나 기여하는지 측정한다. 이전 절에서는 팩터 모멘텀을 통제했을 때 개별 주식 모멘텀이 남아있는지 확인했다면, 이번에는 개별 주식 모멘텀을 통제했을 때 팩터 모멘텀이 얼마나 남아있는지 확인한다.

따라서 모멘텀의 기원을 모멘텀 중립 팩터에서 팩터 모멘텀을 측정함으로써 조사한다.
팩터가 우연적인 모멘텀을 가지려면 다음과 같은 식을 만족해야 한다.
$\sum_{i=1}^{N} w_{i,t} \, r_{i,t-12,t-2} \neq 0$ (즉 w와 r이 서로 무관해야함.)

본 논문에서는 Kozak, Nagel and Santosh(2020)의 팩터를 활용하고 팩터의 과거 수익률과 직교하도록 팩터 가중치를 가능한 한 적게 조정하여 모멘텀 중립 팩터를 구성한다.
→ 새로운 가중치 $x_i$ 를 찾기 위함.

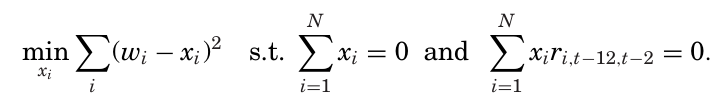
→ 이 문제의 해 $x_i$ 는 원래 가중치 $w_i$ 를 과거 수익에 대해 횡단면 회귀했을 때의 잔차와 동일.
$w_{i,t} = a + b\, r_{i,t-12,t-2} + x_{i,t}$
이 $x_i$ 가중치를 가진 팩터를 모멘텀 중립 팩터라고 부른다. 이는 모든 팩터에 대해 적용된다.

위 회귀식에서의 47개 팩터의 평균 $R^2$ 는 0.4% ~ 10.2% 사이이며, 전체 팩터 평균은 2.4%이다.
→ 이는 표준 팩터 가중치와 모멘텀 중립 가중치가 매우 가깝다는 것을 의미함(독립변수가 설명을 못하여 대부분이 잔차로 이동하기 때문).

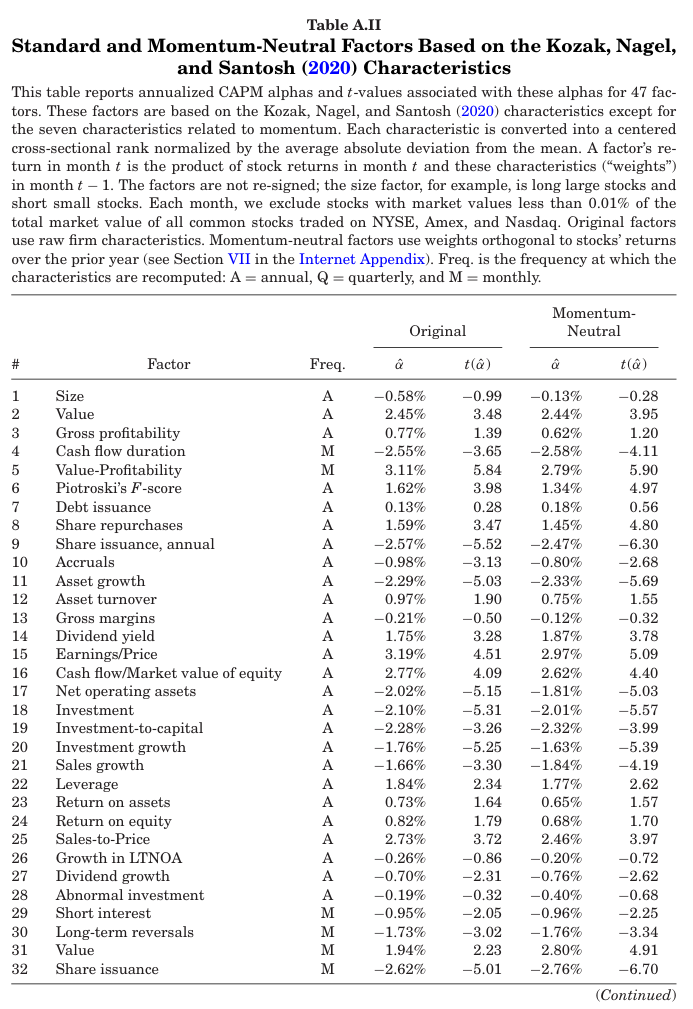
표 A.II는 47개 모멘텀 중립 팩터에 대한 연환산 CAPM 알파를 보여준다(위 사진은 일부분만 존재).
모멘텀 중립 팩터는 일반적으로 표준 팩터와 유사한 프리미엄을 얻지만 변동성이 더 낮기 때문에 더 높은 정보비율을 기록한다(즉 t-statistics가 더 높다).

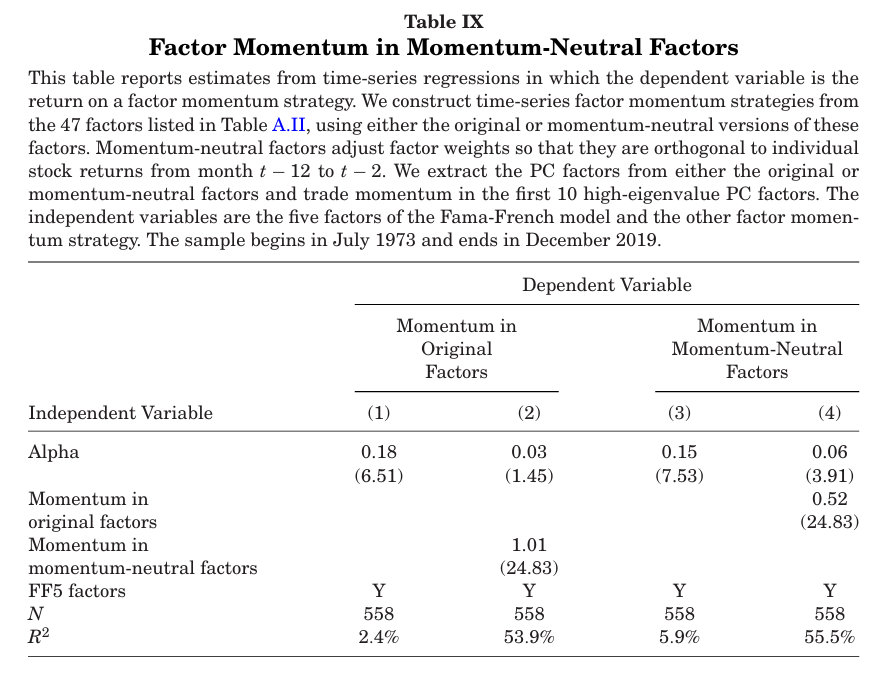
표 10은 모멘텀 중립 팩터를 거래하는 팩터 모멘텀 전략이 표준 팩터를 거래하는 전략보다 수익성이 더 높다는 것을 보여준다.

• 표준 팩터에서 추출한 고유값이 높은 PC1-10 을 거래하는 팩터 모멘텀 전략이 t=6.51을 가지는 반면 모멘텀 중립 PC 팩터를 사용하여 전략을 구성하면 t=7.53으로 더 증가한다.
• 모멘텀 중립 팩터를 통제할 경우, 표준 PC 팩터 모멘텀 전략의 알파는 3bp(t=1.45)인 반면, 팩터 모멘텀을 통제할 경우 모멘텀 중립 PC 팩터 모멘텀 전략의 알파는 6bp(t=3.91)로 여전히 유의하다.
  → 이러한 발견은 팩터 모멘텀이 단순한 우연적 모멘텀이라는 가능성을 배제한다.

6. Conclusion

팩터 수익률에는 양의 자기상관이 광범위하게 존재한다.
지난 1년동안 수익이 좋았던 팩터들은 유의한 프리미엄을 계속 얻는 반면, 수익이 나빴던 팩터들은 통계적으로 0과 구분되지 않는 프리미엄을 얻는다.

팩터 모멘텀은 이러한 팩터 수익의 자기상관에 베팅하는 전략으로, 팩터 모멘텀이 다음의 모멘텀 전략들을 설명함을 보인다.

• Jegadeesh and Titman(1993)의 표준 주식 모멘텀
• 산업 조정 모멘텀
• 산업 모멘텀
• 중간 모멘텀
• 샤프비율 모멘텀
• 세가지 버전의 잔차 모멘텀
  반면 이러한 모멘텀 팩터들은 팩터 모멘텀을 설명하지 못한다.

또한 고유값이 큰 주성분 팩터들에서 발견되는 모멘텀은 다른 모멘텀 및 다른 PC 팩터 모멘텀을 잘 설명하며, 모멘텀이 독립적인 팩터가 아니라 다른 팩터들에서 발견되는 자기상관의 합이라는 결과를 보인다.

추가적으로 KNS 모형을 통해 감성이 충분히 지속될 경우 팩터 모멘텀이 발생한다는 것, 이 경우 모멘텀이 주식 수익률의 횡단면을 더 많이 설명하는 팩터에 집중된다는 것을 보였다.

본 논문에서는 2가지의 향후 발전 요소를 제시한다.

1. 팩터 모멘텀이 KNS 모형의 감성 투자자 가설과 일치한다고 해서 반드시 팩터 모멘텀이 미스프라이싱에서 비롯된다고 결론지을 순 없다.
   만약 시간에 따라 변하는 위험 프리미엄을 갖는 합리적인 모형을 설정한다면, 이 모형은 팩터 모멘텀에 대해 추가적이면서 구별되는 예측을 제시할 수 있을 것이다.

2. 팩터 모멘텀을 통제하면 잔차 모멘텀이 남지 않음을 발견했지만, 이것이 기업 고유 수익이 자기상관을 전혀 갖지 않는다는 것을 결정적으로 증명한 것은 아니다(누락된 팩터 및 추정 베타 문제).
   따라서 팩터 모멘텀과 기업 고유 모멘텀 사이의 최종 결론을 내리기 위해선 기업 고유 수익을 정확하게 추출하거나 식별할 수 있는 방법 및 자연실험을 고안해야 할 것이다.

리뷰를 마치며

이 논문은 팩터 모멘텀 뿐만 아니라 주식 모멘텀과의 관게, 주식 모멘텀의 특성 등을 포괄적으로 다룬 논문인 것 같다. 팩터 모멘텀에 초점을 두었다기 보다는 오히려 주식 모멘텀에 좀 더 초점을 두었다고 느꼈으며, 정말 깊이 있고 엄밀한 실험을 진행했다.
개인적으로 기억에 남는 것은 주식 모멘텀의 수익을 수식으로 풀어서 팩터 로딩으로 인해 발생한다는 것을 보였다는 것이다. 기존 논문들에서는 “여러가지 실험을 해보니 무슨 짓을 해도 팩터 모멘텀이 다른 모멘텀을 포함하더라” 같은 느낌이었다면, 이 논문에서는 그 원인을 이론적으로 풀어낸 것이 인상깊었다. 팩터의 개수도 모멘텀에 영향을 준다는 점 또한 새롭게 알게 된 사실이었다. 역시 탑저널에 실린 논문들은 정말 배워가는 것이 많은 것 같다.