chapter.6 심화 발제: 주성분 분석

주성분 분석(principal component analysis)

주성분 분석이란?
차원 축소(Dimensionality Reduction)의 한 방법으로, 데이터의 패턴을 보존하며 데이터의 차원을 줄이는 방법.


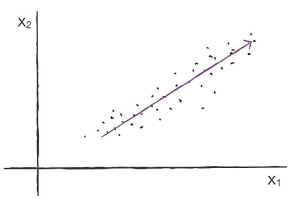
PCA는 데이터의 분산을 최대한 설명하는 새로운 축(주성분)을 찾는다.

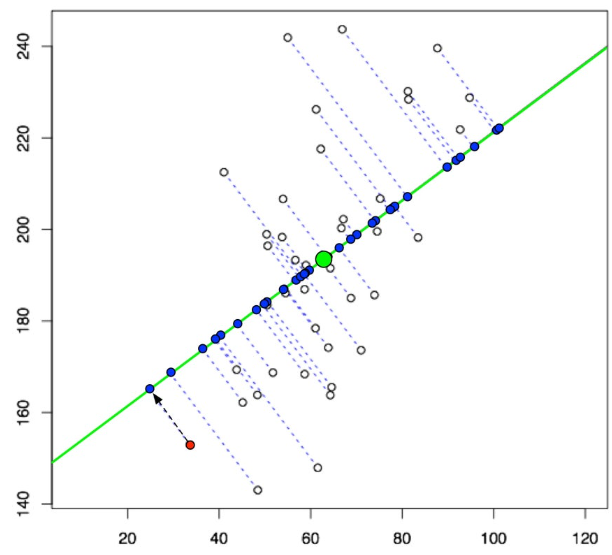
주성분을 찾으면 해당 주성분 방향으로 기존 데이터들을 사영시킨다. 이렇게 각 주성분 축으로 사영된 값들을 주성분 점수(Principal Component Scores)라고 부르며, 이는 원본 데이터가 주성분 방향으로 변환된 결과이다.

첫 번째 주성분(PC1)은 데이터의 가장 큰 분산 방향을 따라가며, 두 번째 주성분(PC2)은 첫 번째 주성분에 직교하면서 그다음으로 큰 분산을 설명한다. 주성분의 개수는 모델의 factor 수보다 클 수 없다.

특이값 분해(Singular Value Decomposition)

행렬을 세 개의 행렬로 분해하는 기법으로 주성분 분석에서 데이터 행렬을 직접 분해하여 주성분을 구할 때 사용된다.
$X=UΣV^T$
$X$: 원본 데이터 행렬. PCA분석에서는 공분산 행렬
$U$: 데이터의 주성분 방향을 나타내는 직교 행렬.
$\sum$: 대각 행렬로, 데이터의 분산을 나타내는 특이값들이 포함되어 있다.
$V^T$: 주성분(새로운 축) 방향을 나타내는 행렬.

여기서, SVD의 결과로 얻어지는 $V^T$행렬의 열 벡터들(고유벡터)이 PCA의 주성분 벡터에 해당한다. 이 벡터들은 원본 데이터의 방향을 변환하는 데 사용됨.

로딩(Loading)과 분산 설명력(Explained Variance)

로딩은 각 원래 변수(특징)가 주성분에 얼마나 기여하는지를 나타내는 값. 로딩은 주성분 벡터의 요소들로, 각 변수와 주성분 간의 상관관계를 설명한다.
주성분 벡터의 각 점수는 기존 팩터들의 선형 결합을 나타내며, 팩터 계수 값이 클수록 해당 팩터가 그 주성분에 더 많이 기여하는 것을 의미한다. $PC_i = a_{i1}X_1 + a_{i2}X_2 + … + a_{in}X_n $
$PC_i$: i번째 주성분 점수
$X_1, X_2, … , X_n$: 기존 팩터
$a_{i1}, a_{i2}, … , a_{in}$: 주성분 벡터의 요소들로 기존 팩터 X의 선형 결합 계수 값이자 주성분의 로딩 값이 된다.

• 로딩의 부호(+, -)는 해당 변수와 주성분 간의 방향성을 나타낸다.
• 주성분 벡터의 로딩 값들은 행렬의 고유벡터의 원소이기 때문에 보통 정규화되어 있어, 로딩의 제곱합이 1이다.

분산 설명력(Explained Variance)은 주성분분석(PCA)에서 각 주성분(Principal Component)이 원본 데이터의 전체 분산 중에서 얼마나 많은 비율을 설명하는지를 나타내는 지표이다.

주성분 분석에서 구해지는 PC1, PC2,…는 기존 데이터의 분산을 가장 잘 설명하는 순으로 정렬된다. 일반적으로 누적 분산 설명력이 70~90%일 때의 주성분들을 선택한다.

이 값을 통해 주성분의 중요성을 평가하고, 적절한 차원 축소를 수행할 수 있다.

PCA 단계

1. 선형성 충족 여부 확인: PCA과정이 변수들 간의 선형결합으로 이루어져있기 때문에 변수들 간의 관계가 선형적이라는 선형성이 충족되어야한다.

2. 데이터 스케일링 진행: 주성분 분석에서 각 팩터간의 스케일이 다르면 값의 오류가 발생할 수 있기 때문에 모든 팩터가 같은 스케일을 가지는 경우가 아니라면 스케일링은 필수로 진행한다.

3. 공분산 행렬 계산: 주어진 데이터에 대해 공분산 행렬을 계산한다.(공분산 행렬은 대칭 행렬이기 때문에 고유값 분해가 항상 가능)

4. 고유값과 고유벡터 계산: 공분산 행렬의 고유값과 고유벡터를 계산한다. 이때 고유값은 주성분이 설명하는 분산의 크기를 나타내며, 고유벡터는 각 주성분의 방향을 나타낸다.

5. 주성분 선택: 고유값의 크기에 따라 주성분을 내림차순으로 정렬하고, 상위 몇 개의 주성분을 선택. 선택된 주성분의 수가 최종 데이터의 차원이 된다.

6. 새로운 데이터 표현: 원래 데이터를 선택된 주성분의 고유벡터들에 사영(projection)하여 새로운 저차원 데이터를 생성. 이 새로운 데이터는 원래 데이터의 주요한 정보(분산)를 유지하면서도 차원이 축소된 형태로 표현된다.

PCA 장&단점

PCA의 장점

1. 차원 축소
   PCA는 데이터의 중요한 정보를 유지하면서 데이터의 차원을 줄일 수 있다. 이는 계산 효율성을 높여주고, 머신러닝 모델에서 과적합(overfitting)을 방지하는 데 도움이 된다.

2. 다중공선성 방지
   상관관계가 높은 팩터들의 관계를 서로 독립적인 주성분으로 변환하기 때문에 기존 팩터 값이 아닌 주성분 값을 독립변수로 설정하여 회귀분석을 진행하면 다중공선성 문제를 해결할 수 있음.

PCA의 단점

1. 해석의 어려움
   PCA는 원래 변수들의 선형 결합으로 새로운 주성분을 생성하지만, 이 주성분이 무엇을 의미하는지는 알기 어려움. 예를 들어 생선의 길이, 무게, 색깔 등의 특성 값으로 주성분 분석을 실시했을 때 도출된 주성분이 어떤 성격을 지니고있는지 직관적으로 파악하기 어렵다.

2. 부호의 무작위성
   주성분 값의 선형 결합 결과가 기존 팩터들이 가지는 데이터의 성격과 완전히 정반대의 값이 나올 수 있음. 따라서 기존 팩터들과 정반대의 형태를 가지고 있다면 수동적으로 부호를 반대로 설정해줘야 한다.

3. 대표성의 한계
   주성분이 모든 특성을 대표한다고는 하지만, 이는 그 특성들의 “주요 변동성”을 대표하는 것이지 각 특성의 원래 값을 그대로 반영하는 것은 아니다. 따라서 주성분 분석에 활용하는 모든 특성이 같은 성격을 가지고 있더라도 주성분 값의 크기는 기존 데이터의 의미를 왜곡할 수 있다.

주성분 분석을 활용한 미국 시장 분석

위에서 설명한 주성분 분석을 활용하여 간단하게 미국 주식 시장을 판단하는 지표를 출력해볼 것이다.

미국 시장을 잘 대표하는 지수들이 많이 존재하긴 하지만 이러한 지수들을 주성분 분석으로 하나의 주성분으로 추출하여 하나만의 지표로 미국 시장을 파악할 수 있도록 하는 것이 목표

import yfinance as yf
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA

# 미국 시장을 대표하는 시장 지수 다운로드 (Dow Jones, S&P 500, Nasdaq, Russell 2000)
tickers = ["^DJI", "^GSPC", "^IXIC", "^RUT", "^W5000", "^OEX", "^MID", "^NDX"]
data = yf.download(tickers, period="4y")['Adj Close']

# 월평균 수익률 계산
returns = data.pct_change().dropna()
monthly_returns = returns.resample('M').mean()

먼저 미국 시장을 대표하는 유명한 지수들(Dow Jones, S&P 500, Nasdaq, Russell 2000)의 4년동안의 데이터를 다운로드하고 월평균 수익률을 계산한다.

# 주성분 분석 진행
pca = PCA(n_components=1)
pc1 = pca.fit_transform(monthly_returns)

results_df = pd.DataFrame(monthly_returns, columns=tickers)
results_df['PC1'] = pc1.flatten()

explained_variance_ratio = pca.explained_variance_ratio_[0]
print(f"Explained Variance Ratio of PC1: {explained_variance_ratio:.2%}")
# output: Explained Variance Ratio of PC1: 86.88%

주성분 분석을 진행하여 가장 분산 설명력이 좋은 PC1을 추출한다. PC1이 전체 데이터의 분산의 86.88%를 설명하고 있으므로 하나의 주성분 만으로도 데이터의 분산을 설명할 수 있다고 판단할 수 있음.

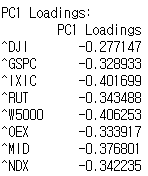
loadings = pca.components_[0]
loadings_df = pd.DataFrame(loadings, index=tickers, columns=['PC1 Loadings'])

print("\nPC1 Loadings:")
print(loadings_df)

# 월평균 수익률 그래프 출력
plt.figure(figsize=(14, 8))

plt.subplot(2, 1, 1)
for ticker in tickers:
    plt.plot(monthly_returns.index, monthly_returns[ticker], label=f'{ticker} Monthly Returns')

plt.plot(results_df.index, results_df['PC1'], label='PC1 Monthly Returns', color='orange', linestyle='--')

plt.title('Monthly Returns of Major US Market Indices with PC1')
plt.legend()
plt.show()

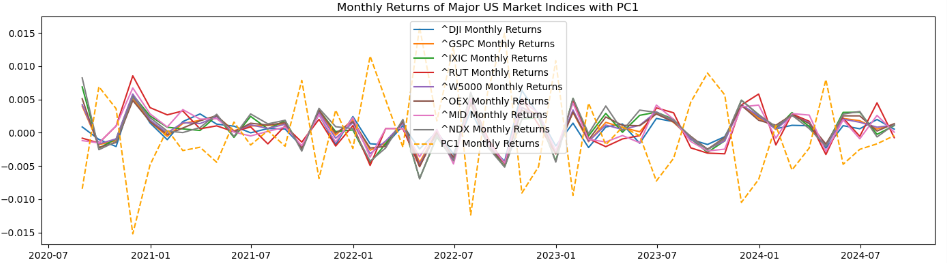
기존 시장 지수들과는 완전히 정반대의 형태를 띄고 있음을 알 수 있음. → 주성분 값의 부호를 바꿔야 한다.

pca = PCA(n_components=1)
# 주성분 값에 부호 변경
pc1 = -pca.fit_transform(monthly_returns)

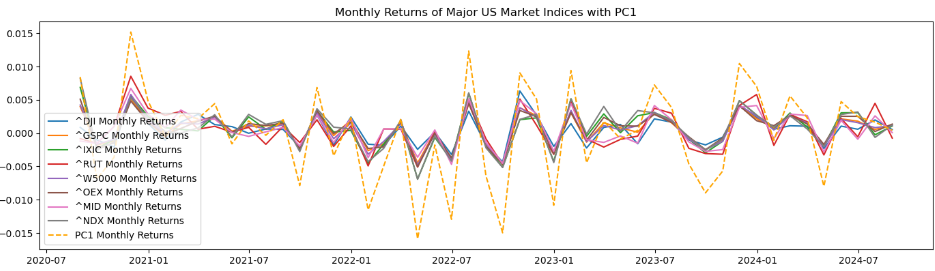
→ 그래프 형태는 거의 비슷하지만 PC1 그래프가 훨씬 더 극단적으로 나타난다.

# 기간별 팩터들과 PC1 값 출력
print(results_df)

이렇게 하면 각 기간별로 시장 지수들과 PC1값이 출력되는데 2024-05-31 데이터의 경우 각각 0.001061 0.002151 0.003057 0.002205 0.002044 0.002536 0.001928 0.002801 0.004743로 출력된다. 가장 마지막 값이 PC1 값인데 다른 지수들의 수익률이 모두 0.1~0.3%을 기록하는 반면 PC1 값은 0.4%를 기록하는 것을 볼 수 있음. 이렇게 기존 팩터 값보다 더 극단적인 값이 도출될 수 있다.

# 4년간의 누적수익률 계산
cumulative_returns = (1 + monthly_returns).cumprod() - 1

plt.subplot(2, 1, 2)
for ticker in tickers:
    plt.plot(cumulative_returns.index, cumulative_returns[ticker], label=f'{ticker} Cumulative Returns')

plt.plot(cumulative_returns.index, (1 + results_df['PC1']).cumprod() - 1, label='PC1 Cumulative Returns', color='orange', linestyle='--')

plt.title('Cumulative Returns of Major US Market Indices with PC1')
plt.legend()

plt.tight_layout()
plt.show()

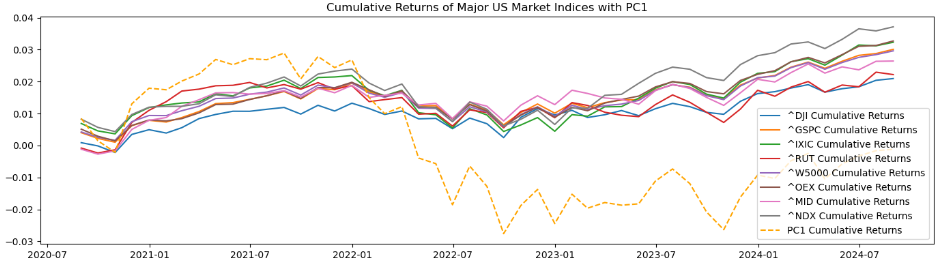
누적수익률 그래프를 보면 다른 시장 지수들과 비슷한 형태를 띄고 있긴 하지만 전반적으로 값이 매우 다름
→ 주성분 값: $PC_i = a_{i1}X_1 + a_{i2}X_2 + … + a_{in}X_n$ 에서 각 로딩의 제곱합이 1인 것이지 값의 합이 1인 것은 아니기에 기존 팩터들의 데이터들로 주성분 분석을 실시하여 계산된 PC1값이 기존 팩터 데이터들보다 훨씬 크거나 작게 출력된다(각 팩터의 로딩이 모두 동일한 부호이기 때문). 따라서 주성분 값의 크기에 왜곡이 일어나 미국 시장 지수를 대표한다고 보기 어려움.

기타 방법론 소개

1. 독립 성분 분석(ICA, Independent Component Analysis)
   PCA와 유사하게 차원 축소를 위한 기법이지만, 데이터의 분산을 최대화하는 대신, 서로 독립적인 성분들을 추출하는 것을 목표로 한다. ICA는 데이터가 비정규 분포를 가질 때 유용

2. PLS(Partial Least Squares Regression)
   독립 변수와 종속 변수 간의 공통된 구조를 찾기 위해 데이터를 변환하는 방법. 즉 PCA는 X의 분산을 최대화하는 데 중점을 두는 반면 PLS는 X와 Y의 상관관계를 최대화하는 성분을 찾는 데 중점을 둔다.
   → 회귀 분석에서 PCA의 단점(궁극적인 통계적 목표의 불일치)를 개선할 수 있음.