chapter.3 회귀 알고리즘과 모델 규제

Posted Jul 31, 2024 Updated Aug 4, 2024

By AhnHyoungMin

18 min read

3.1 k-최근접 이웃 회귀

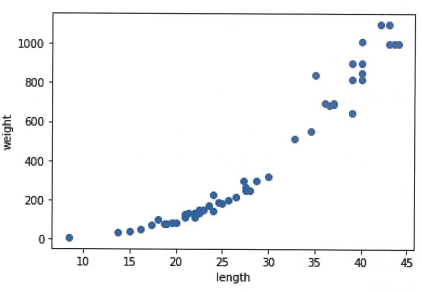
농어 길이 데이터만으로 무게 예측하기 → 농어의 길이가 특성, 무게가 타깃

  
import numpy as np
perch_length = np.array([8.4, 13.7, 15.0, 16.2, 17.4, 18.0, 18.7, 19.0, 19.6, 20.0, 21.0,
       21.0, 21.0, 21.3, 22.0, 22.0, 22.0, 22.0, 22.0, 22.5, 22.5, 22.7,
       23.0, 23.5, 24.0, 24.0, 24.6, 25.0, 25.6, 26.5, 27.3, 27.5, 27.5,
       27.5, 28.0, 28.7, 30.0, 32.8, 34.5, 35.0, 36.5, 36.0, 37.0, 37.0,
       39.0, 39.0, 39.0, 40.0, 40.0, 40.0, 40.0, 42.0, 43.0, 43.0, 43.5,
       44.0])
perch_weight = np.array([5.9, 32.0, 40.0, 51.5, 70.0, 100.0, 78.0, 80.0, 85.0, 85.0, 110.0,
       115.0, 125.0, 130.0, 120.0, 120.0, 130.0, 135.0, 110.0, 130.0,
       150.0, 145.0, 150.0, 170.0, 225.0, 145.0, 188.0, 180.0, 197.0,
       218.0, 300.0, 260.0, 265.0, 250.0, 250.0, 300.0, 320.0, 514.0,
       556.0, 840.0, 685.0, 700.0, 700.0, 690.0, 900.0, 650.0, 820.0,
       850.0, 900.0, 1015.0, 820.0, 1100.0, 1000.0, 1100.0, 1000.0,
       1000.0])

import matplotlib.pyplot as plt
plt.scatter(perch_length, perch_weight)
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

  
from sklearn.model_selection import train_test_split

train_input, test_input, train_target, test_target = train_test_split(
    perch_length, perch_weight, random_state=42)

# reshape()함수를 사용하여 배열을 2차원으로 변경 
train_input = train_input.reshape(-1,1)
test_input = test_input.reshape(-1,1)

※ 결정계수($R^2$)

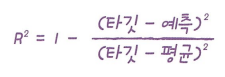
회귀분석에서 모델의 설명력을 나타내는 지표로 활용. 1에 가까울수록 좋음.

  
from sklearn.metrics import mean_absolute_error

# 테스트 세트에 대한 예측을 만듭니다
test_prediction = knr.predict(test_input)

# 테스트 세트에 대한 평균 절댓값 오차를 계산합니다
mae = mean_absolute_error(test_target, test_prediction)
print(mae) # output: 19.157142

타깃과 예측한 값 사이의 차이를 구해봄으로써 어느 정도 예측이 벗어났는지 가늠할 수 있음
→ 약 19g정도 타깃값과 다르다는 것을 알 수 있다.

train set과 test set을 사용해 각각 평가 진행

  
print(knr.score(train_input, train_target)) # output: 0.9698 
print(knr.score(test_input, test_target))  
# output: 0.992

보통 훈련 세트로 모델을 학습시키기 때문에 훈련 세트에서 더 좋은 점수가 산출됨
→ 만약 훈련 세트에서 점수가 좋은데 테스트 세트에서는 점수가 나쁘다면 모델이 훈련 세트에 과적합(overfitting)되었다고 함. 반대로 훈련 세트보다 테스트 세트의 점수가 높거나 두 점수가 둘 다 낮은 경우에는 모델이 훈련 세트에 과소적합(underfitting)되었다고 함.

과소적합이 일어나는 원인으로는 훈련 세트와 테스트 세트의 크기가 매우 작은 경우가 있음

따라서 위 문제에서 일어난 과소적합을 해결하기 위해 모델을 조금 더 복잡하게 만들자
→ k-최근접 이웃 알고리즘으로 모델을 더 복잡하게 만드는 방법은 이웃의 개수 k를 줄이는 것

  
# 이웃의 개수를 3으로 설정합니다
knr.n_neighbors = 3

# 모델을 다시 훈련합니다
knr.fit(train_input, train_target)
print(knr.score(train_input, train_target)) # output: 0.98
print(knr.score(test_input, test_target)) # output: 0.9746  

3-2 선형 회귀

  
print(knr.predict([[50]])) # output: [1033.333]

모델은 50cm 농어의 무게를 1033g정도로 예측했으나 실제 이 농어의 무게는 훨씬 더 많이 나감.

원인 확인을 위해 산점도 표시

  
import matplotlib.pyplot as plt

# 50cm 농어의 이웃을 구합니다
distances, indexes = knr.kneighbors([[50]])

# 훈련 세트의 산점도를 그립니다
plt.scatter(train_input, train_target)

# 훈련 세트 중에서 이웃 샘플만 다시 그립니다
plt.scatter(train_input[indexes], train_input[indexes], marker='D')

# 50cm 농어 데이터
plt.scatter(50, 1033, marker='^')
plt.show()

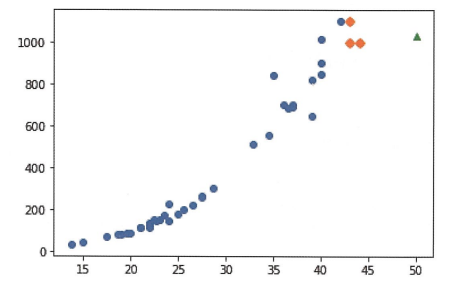
길이가 50cm이고 무게가 1033g인 농어는 삼각형으로 표시되고 그 주변의 샘플은 마름모로 표시. 50cm 농어에서 가장 가까운 데이터가 45cm 근방이기 때문에 k-최근접 이웃 알고리즘은 이 샘플들의 무게를 평균한다.
→ 따라서 새로운 샘플이 훈련 세트의 범위를 벗어나면 엉뚱한 값을 예측할 수 있음(ex. 100cm 농어도 1033g으로 예측)

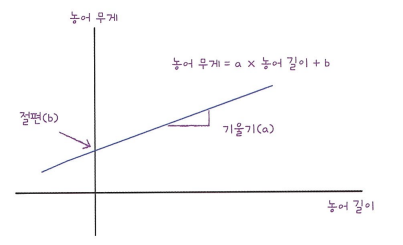
※ 선형 회귀

특성이 하나인 경우 데이터를 가장 잘 표현하는 직선을 학습하는 알고리즘

  
from sklearn.linear_model import LinearRegression

lr = LinearRegression()

# 선형 회귀 모델을 훈련합니다
lr.fit(train_input, train_target)

# 50cm 농어에 대해 예측합니다
print(lr.predict([[50]])) # output: [1241.83860323]

→ k-최근접 이웃 회귀를 사용했을 때와 달리 선형 회귀는 농어의 무게를 더 높게 예측함

  
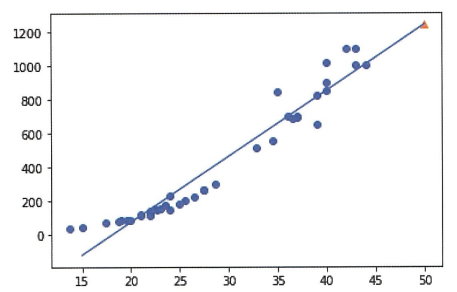
print(lr.coef_, lr.intercept_) # 직선의 기울기, y절편값 확인

# 훈련 세트의 산점도를 그립니다
plt.scatter(train_input, train_target)

# 15에서 50까지 1차 방정식 그래프를 그립니다
plt.plot([15, 50], [15*lr.coef_ + lr.intercept_, 50*lr.coef_ + lr.intercept_])

# 50cm 농어 데이터
plt.scatter(50, 1241.8, marker='^')
plt.show()

  
print(lr.score(train_input, train_target)) # 훈련 세트
print(lr.score(test_input, test_target)) # 테스트 세트
# output: 0.9398
#         0.8247

→ 훈련 세트의 $R^2$ 값도 그렇게 높게 나오지 않았음. 전체적으로 과소적합되었음. 또한 농어 데이터의 산점도를 보면 직선보다는 곡선 형태에 가까움

※ 다항 회귀

  
# column_stack()함수를 사용하여 농어의 길이를 제곱해서 원래 데이터 앞에 붙이기  
train_poly = np.column_stack((train_input**2, train_input))
test_poly = np.column_stack((test_input**2, test_input))

print(train_poly.shape, test_poly.shape)
# output: (42,2) (14,2)

  
lr = LinearRegression()
lr.fit(train_poly, train_target)

print(lr.predict([[50**2, 50]])) # output: [1573.9842]
print(lr.coef_, lr.intercept_) # output: [1.014 -21.5579] 116.05

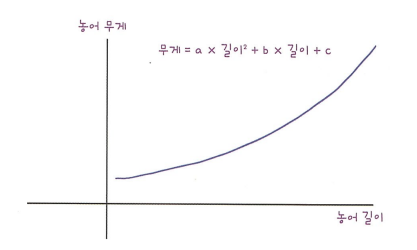
→ 이 모델은 다음과 같은 그래프를 학습함.
$무게 = 1.01 * 길이^2 - 21.6*길이 + 116.05$

이런 방정식을 다항식이라 부르며 다항식을 사용한 선형 회귀를 다항 회귀 라고 부름

  
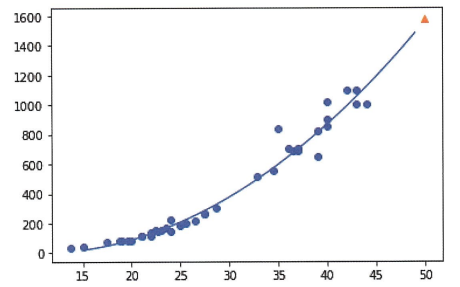
# 구간별 직선을 그리기 위해 15에서 49까지 정수 배열을 만듭니다
point = np.arange(15, 50)

# 훈련 세트의 산점도를 그립니다
plt.scatter(train_input, train_target)

# 15에서 49까지 2차 방정식 그래프를 그립니다
plt.plot(point, 1.01*point**2 - 21.6*point + 116.05)

# 50cm 농어 데이터
plt.scatter([50], [1574], marker='^')
plt.show()

  
print(lr.score(train_input, train_target)) # 훈련 세트
print(lr.score(test_input, test_target)) # 테스트 세트
# output: 0.9706
#         0.9775

→ 더 좋아졌지만 여전히 테스트 세트의 점수가 더 높아 과소적합이 남아있음.

3-3 특성 공학과 규제

다항 회귀로 농어의 무게를 어느정도 예측할 수 있지만, 여전히 훈련 세트보다 테스트 세트의 점수가 높음. 이러한 문제를 해결하려면 제곱보다 더 고차항을 넣어야 하는데 그 기준이 애매함.

이 예제에서는 농어의 길이뿐만 아니라 농어의 높이와 두께도 함께 사용하여 3개의 특성을 활용. 또한 각 특성을 서로 곱해서 또다른 특성을 생성. 이렇게 기존의 특성을 사용하여 새로운 특성을 뽑아내는 작업을 특성 공학이라고 부른다.

판다스 라이브러리를 활용하여 농어 데이터를 인터넷에서 다운받아 데이터프레임에 저장한다. 이때 read_csv()함수로 데이터프레임을 만든 다음 to_numpy()함수를 사용하여 넘파이 배열로 변경해준다.

  
import pandas as pd  # pd는 관례적으로 사용하는 판다스의 별칭입니다

df = pd.read_csv('https://bit.ly/perch_csv')
perch_full = df.to_numpy()
print(perch_full)
# output: [[8.4 2.11 1.41]]
#          [13.7 3.53 2. ]
#          ...
#          [44. 12.49 7.6]

※ 사이킷런의 변환기
사이킷런은 특성을 만들거나 전처리하기 위한 다양한 클래스를 제공하는데 이러한 클래스를 변환기라고 부른다. 우리가 사용할 변환기는 PolynomialFeatures 클래스이다.

  
from sklearn.preprocessing import PolynomialFeatures

# 2개의 특성 2와3으로 이루어진 샘플 적용
poly = PolynomialFeatures()
poly.fit([[2,3]])
print(poly.transform([[2,3]]))
# output: [[1. 2. 3. 4. 6. 9.]]

훈련(fit)을 해야 변환이 가능하다는 점을 주의!

2,3을 각각 제곱한 4와9가 추가되었고 2와3을 곱한 6이 추가되었으며 방정식의 절편의 계수인 1까지 추가됨. 이때는 include_bias=False로 지정하여 다시 특성을 변환할 수 있음

  
from sklearn.preprocessing import PolynomialFeatures

poly = PolynomialFeatures(include_bias=False)
poly.fit([[2, 3]])
print(poly.transform([[2, 3]])) # output: [[2. 3. 4. 6. 9.]]

이 방식으로 train_input에 적용

  
from sklearn.preprocessing import PolynomialFeatures

poly = PolynomialFeatures(include_bias=False)
poly.fit(train_input)
train_poly = poly.transform(train_input)
print(train_poly.shape) # output: (42,9)

# 9개의 특성이 각각 어떤 입력의 조합으로 만들어졌는지 확인
poly.get_feature_names()
# output: ['x0', 'x1', 'x2', 'x0^2', 'x0 x1', 'x0 x2', 'x1^2', 'x1 x2', 'x2^2']

# 테스트 세트 변환
test_poly = poly.transform(test_input)

  
from sklearn.linear_model import LinearRegression

lr = LinearRegression()
lr.fit(train_poly, train_target)
print(lr.score(train_poly, train_target))
# output: 0.99
print(lr.score(test_poly, test_target))
# output: 0.97

→ 과소적합 문제 해결

5제곱까지 특성을 만들어보면 어떨까?

  
from sklearn.preprocessing import PolynomialFeatures

poly = PolynomialFeatures(degree=5, include_bias=False)
poly.fit(train_input)
train_poly = poly.transform(train_input)
test_poly = poly.transform(test_input)
print(train_poly.shape)
# output: (42,55)

→ 만들어진 특성 개수가 55개.

  
lr.fit(train_poly, train_target)
print(lr.score(train_poly, train_target))
# output: 0.99999
print(lr.score(test_poly, test_target))
# output: -144.405

특성 개수를 크게 늘렸기 때문에 훈련 세트에 대해서는 거의 완벽하게 학습했지만 훈련 세트에 너무 과대적합되어 테스트 세트에서는 굉장히 낮은 점수가 나옴 4

※ 규제(regularization)
규제는 머신러닝 모델이 훈련 세트를 너무 과도하게 학습하지 못하도록 훼방하여 훈련세트에 과대적합되지 않도록 하는 것을 의미한다.

  
from sklearn.preprocessing import StandardScaler

ss = StandardScaler()
ss.fit(train_poly)
train_scaled = ss.transform(train_poly)
test_scaled = ss.transform(test_poly)

→ 표준점수로 정규화를 진행한 후 변환

선형 회귀 모델에 규제를 추가한 모델을 릿지(ridge)와 라쏘(lasso)라고 부른다. 릿지는 계수를 제곱한 값을 기준으로 규제를 적용하고 라쏘는 계수의 절댓값을 기준으로 규제를 적용한다.(일반적으로 릿지를 조금 더 선호)
두 알고리즘 모두 계수의 크기를 줄이지만 라쏘는 아예 0으로 만들 수도 있음

※ 릿지 회귀

  
from sklearn.linear_model import Ridge

ridge = Ridge()
ridge.fit(train_scaled, train_target)
print(ridge.score(train_scaled, train_target)) # output: 0.9896
print(ridge.score(test_scaled, test_target)) # output: 0.979

→ 확실히 많은 특성을 사용했음에도 불구하고 훈련 세트에 너무 과대적합되지 않은 것을 볼 수 있음

릿지와 라쏘 모델을 사용할 때 규제의 양을 임의로 조절할 수 있다. 모델 객체를 만들 때 alpha매개변수로 규제의 강도 조절. alpha값이 크면 규제 강도를 높이는 것이므로 과소적합될 가능성이 큼

적절한 alpha값을 찾는 방법은 alpha값에 대한 $R^2$값의 그래프를 그려보는 것.
훈련 세트와 테스트 세트의 점수가 가장 가까운 지점이 최적의 alpha값

  
import matplotlib.pyplot as plt
train_score = []
test_score = []

# alpha값을 0.001에서 10배씩 늘려가며 릿지 회귀 모델 훈련
alpha_list = [0.001, 0.01, 0.1, 1, 10, 100]
for alpha in alpha_list:
    # 릿지 모델을 만듭니다
    ridge = Ridge(alpha=alpha)
    
    # 릿지 모델을 훈련합니다
    ridge.fit(train_scaled, train_target)
    
    # 훈련 점수와 테스트 점수를 저장합니다
    train_score.append(ridge.score(train_scaled, train_target))
    test_score.append(ridge.score(test_scaled, test_target))

plt.plot(np.log10(alpha_list), train_score)
plt.plot(np.log10(alpha_list), test_score)
plt.show()

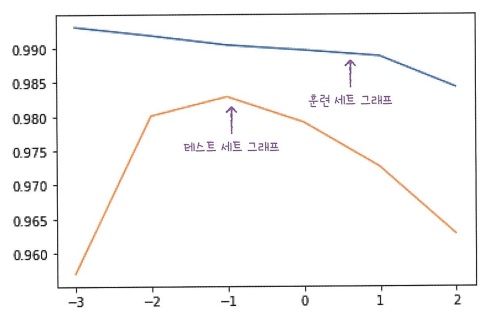
훈련 세트와 테스트 세트 점수 차이가 큰 것을 볼 수 있음. → 전형적인 과대적합 상황
반대로 오른쪽 편은 두 세트의 점수가 모두 낮아지는 과소적합으로 가는 모습을 보이고 있음
적절한 alpha값은 두 그래프가 가장 가깝고 테스트 세트의 점수가 가장 높은 0.1이다.

  
ridge = Ridge(alpha=0.1)
ridge.fit(train_scaled, train_target)

print(ridge.score(train_scaled, train_target)) # output: 0.99
print(ridge.score(test_scaled, test_target)) # output: 0.98

※ 라쏘 회귀

  
from sklearn.linear_model import Lasso

lasso = Lasso()
lasso.fit(train_scaled, train_target)
print(lasso.score(train_scaled, train_target)) # output: 0.9897
print(lasso.score(test_scaled, test_target)) # output: 0.98

→ 라쏘 또한 테스트 세트의 점수가 릿지만큼 좋음

  
train_score = []
test_score = []

alpha_list = [0.001, 0.01, 0.1, 1, 10, 100]

for alpha in alpha_list:
    # 라쏘 모델을 만듭니다
    lasso = Lasso(alpha=alpha, max_iter=10000)
    
    # 라쏘 모델을 훈련합니다
    lasso.fit(train_scaled, train_target)
    
    # 훈련 점수와 테스트 점수를 저장합니다
    train_score.append(lasso.score(train_scaled, train_target))
    test_score.append(lasso.score(test_scaled, test_target))

plt.plot(np.log10(alpha_list), train_score)
plt.plot(np.log10(alpha_list), test_score)
plt.show()

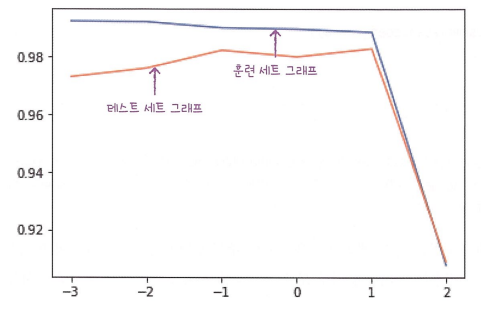
위 그래프 또한 왼쪽은 과대적합, 오른쪽은 과소적합되는 형태를 띄고 있음
라쏘 모델에서 최적의 alpha값은 1

  
lasso = Lasso(alpha=10)
lasso.fit(train_scaled, train_target)
print(lasso.score(train_scaled, train_target)) # output: 0.9888
print(lasso.score(test_scaled, test_target)) # output: 0.9824

  
# 라쏘 모델에서 0이 된 계수 확인
print(np.sum(lasso.coef_ == 0)) # output: 40

55개의 특성을 모델에 넣었지만 라쏘 모델이 사용한 특성은 15개에 불과함
→ 이러한 특징 때문에 라쏘 모델을 유용한 특성을 골라내는 용도로도 사용할 수 있음

KHUDA, ML

KHUDA ML

This post is licensed under CC BY 4.0 by the author.

chapter.3 회귀 알고리즘과 모델 규제

3.1 k-최근접 이웃 회귀

3-2 선형 회귀

3-3 특성 공학과 규제

Trending Tags