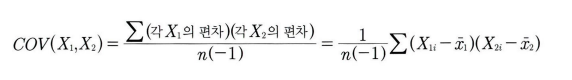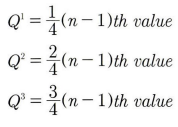Post

데이터 탐색과 시각화

Posted Updated
By AhnHyoungMin
22 min read
데이터 탐색과 시각화

※ EDA VS 데이터 시각화
EDA

  • 데이터를 탐색하고 이해하는 과정.
  • 데이터의 구조와 특징을 파악하여 인사이트를 얻는 것이 주 목적.
    데이터 시각화
  • 데이터를 시각적으로 표현하여 정보를 명확하고 직관적으로 전달하는 것.
  • 복잡한 데이터 세트를 이해하고, 인사이트를 효과적으로 전달.

10.1 탐색적 데이터 분석

EDA의 주요 목적

  • 데이터의 형태와 척도가 분석에 알맞게 되어있는지 확인
  • 데이터의 평균,분산,분포,패턴 등의 확인을 통해 데이터 특성 파악
  • 데이터의 결측값이나 이상치 파악 및 보완
  • 변수 간의 관계성 파악
  • 분석 목적과 방향성 점검 및 보정

10.1.1 엑셀을 활용한 EDA

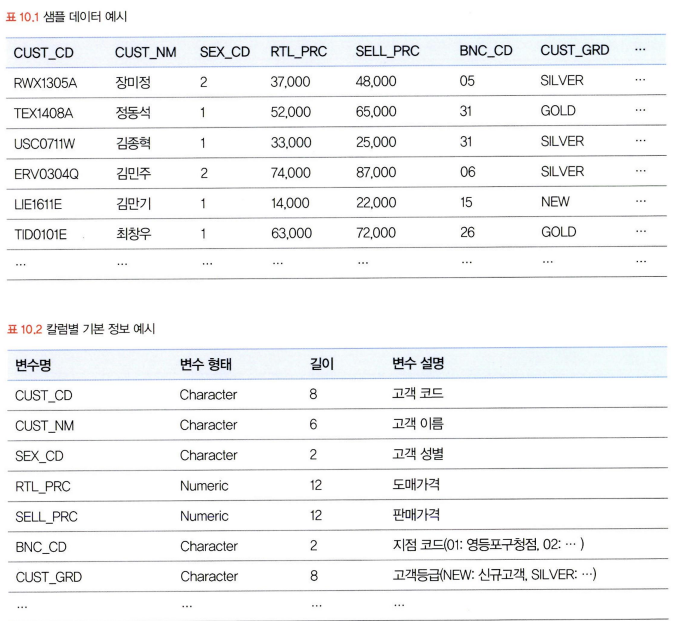
image1.png
김종혁 고객의 경우 도매가격보다 판매가격이 낮게 기록되어있음. → 발견한 데이터 이슈들을 리스트화에서 실무자들과의 미팅을 통해 해결 가능

10.1.2 탐색적 데이터 분석 실습

image1.png

1
2

df = pd.read_csv("")  
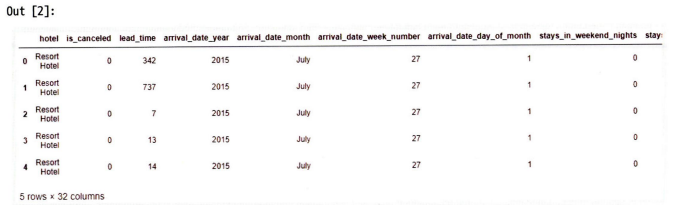
df.head()

image1.png

1

df.info()

→ 데이터에 대한 전반적인 정보를 나타냄. 데이터를 구성하는 행&열 크기와 각 칼럼을 구성하는 값의 자료형 등 확인 가능.
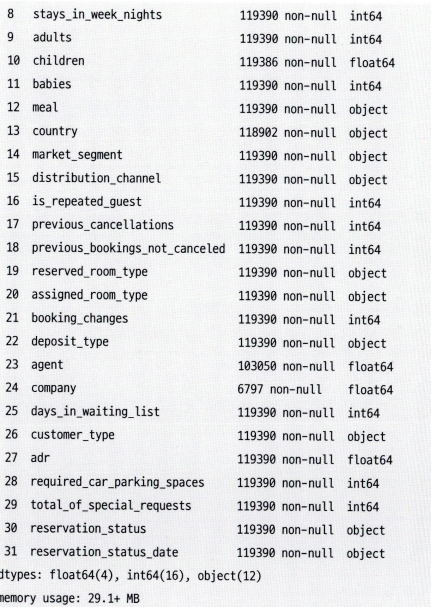image1.png Children 칼럼의 경우 4건의 결측값 존재, company 칼럼은 90%이상이 결측값.

1

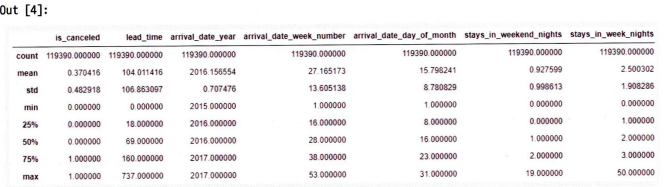
df.describe()

→ 평균,표준편차,최대 최솟값 등을 한번에 확인할 수 있음
image1.png

1
2

df.skew()  
df. kurtosis()

→ 왜도와 첨도 확인

1

sns.displot(df['lead_time'])  # 특정 변수 분포 시각화

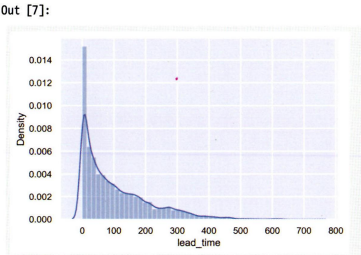image1.png lead_time: 예약 날짜로부터 투숙 날짜까지의 일수 차이
0값이 확연히 많은 것으로 보아 당일 체크인하는 투숙객이 많은 편이라는 것을 확인할 수 있으나 시스템상 기록 오류인 건을 일괄적으로 0으로 입력한 것인지 확인 필요.

1
2

sns.violinplot(x="hotel", y="lead_time", data=df, inner=None, color=".8")  
sns.stripplot(x="hotel", y="lead_time", data=df, size=1)

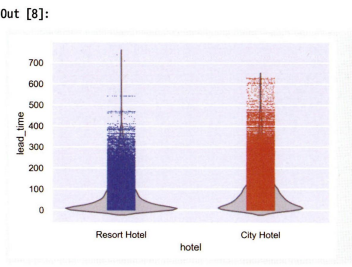
image1.png
Violinplot(): 분포를 효과적으로 표현해줌.
stripplot(): 각 관측치의 위치를 직관적으로 표현해줌.

10.2 공분산과 상관성 분석

데이터 탐색 과정에서 가장 중요한 것 중 하나는 변수 간의 관계를 파악하는 것.
타깃변수 Y와 입력변수 X와의 관계 뿐만 아니라 X들 간의 관계도 살펴봐야 함. → 다중공선성 방지

  • 변수 간의 상관관계를 파악하는 대표적인 개념으로 공분산과 상관계수가 있음.

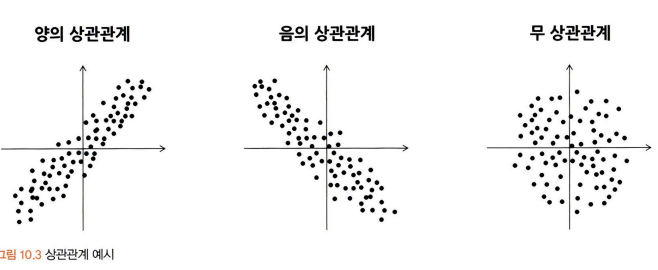
image1.png

  • 양의 상관관계: $X_1$이 커지면 $X_2$도 커진다.
    = 음의 상관관계: $X_1$이 커지면 $X_2$는 작아진다.
  • 무 상관관계: $X_1$과 $X_2$는 선형적인 관계가 없다.

10.2.1 공분산

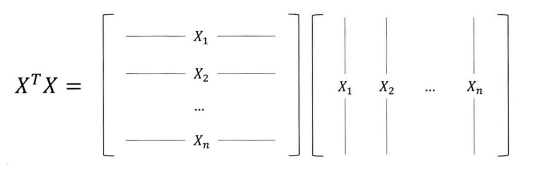
image1.png

  • 주대각 원소는 분산 값을 나타냄.

image1.png

10.2.2 상관계수

$P(X_1,X_2) = \frac{Cov(X_1,X_2)}{\sqrt{Var(X_1)Var(X_2)}}$

  • 직선의 기울기와 상관계수는 직접적인 관련이 없음. 즉 상관계수 값이 모두 같아도 기울기는 다 다를수 있음. 상관계수는 기울기를 측정하는 지표가 아니라 설명력을 나타내는 지표.

결정변수 $R^2$: 회귀분석의 정확도를 가늠하는 중요한 기준 값. 상관계수를 제곱한 값과 동일(단순선형회귀분석에서만 적용)

  • 따라서 상관분석을 할 때는 상관계수만 비교하는 것이 아니라 산점도 그래프를 그려보는 것이 중요함.

image1.png

10.2.3 공분산과 상관성 분석 실습

image1.png
image1.png

1
2

df.cov()  
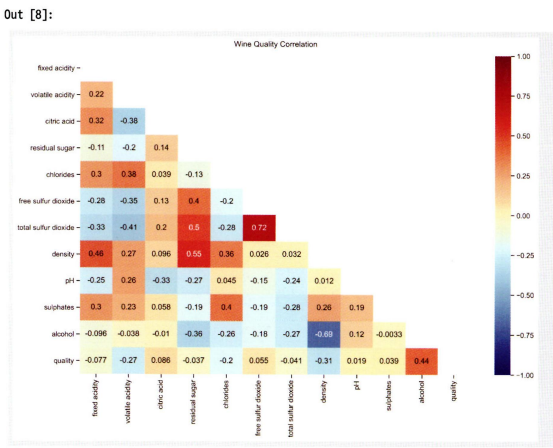
df.corr(method='pearson')
  • 상관계수는 -1~1 값을 가짐. 동일한 변수 간에는 두 값 모두 1
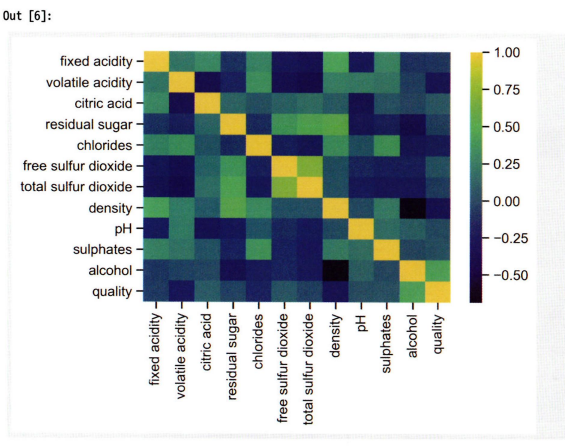
1

sns.heatmap(df.corr(), cmap='viridis')

image1.png

image1.png
image1.png

10.3 시간 시각화

시점 요소가 있는 데이터의 시간 흐름에 따른 변화 표현.

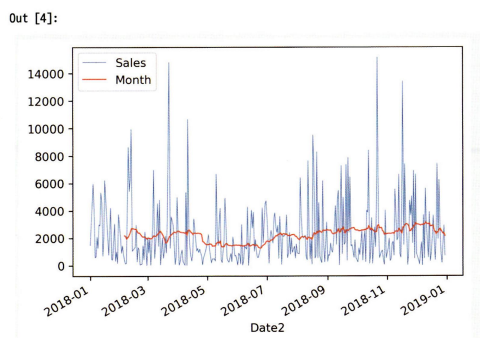
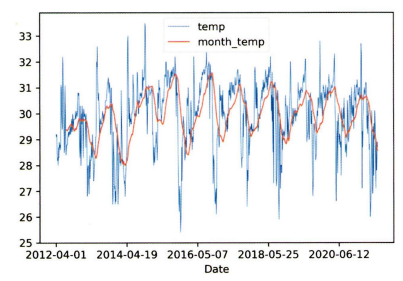
선그래프 VS 이동평균선

  • 시간 간격의 밀도가 높을 때 선그래프 사용. 하지만 데이터의 양이 너무 많거나 변동이 심할 경우 패턴 파악이 어려움.
  • 이동평균선은 들쭉날쭉한 데이터 흐름을 안정된 선으로 표현할 수 있음.
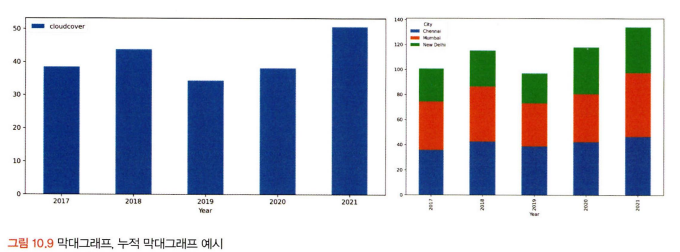
    image1.png

분절형 시간 시각화는 막대그래프, 누적 막대그래프, 점 그래프 등으로 표현.
1년 동안의 월 간격 단위 흐름 등과 같이 시간의 밀도가 낮은 경우에 효율적.
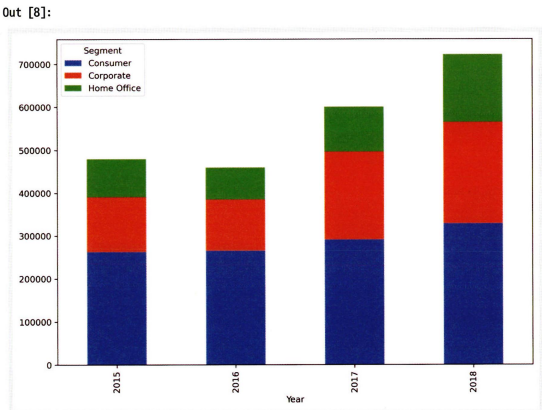
누적 막대그래프는 한 시점에 2개 이상의 세부 항목이 존재할 때 사용.
image1.png

10.3.1 시간 시각화 실습

※ 선그래프 시각화

1
2
3
4
5
6
7
8
9
10
11

df['Date2'] = pd.to_datetime(df['Order Date'], inter_datetime_format=True)  # date칼럼 날짜 형식 변환  

df = df.sort_values(by='Date2')  

df['Year'] = df['Date2'].dt.year  # 연도 칼럼 생성  

df_line = df[df.Year == 2018]   # 2018 데이터만 필터링  

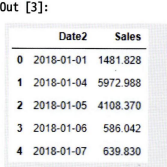
df_line = df_line.groupby('Date2')['Sales'].sum().reset_index()  # 2018년 일별 매출액 가공  

df_line.head()

image1.png

image1.png image1.png

※ 막대그래프 시각화

1
2

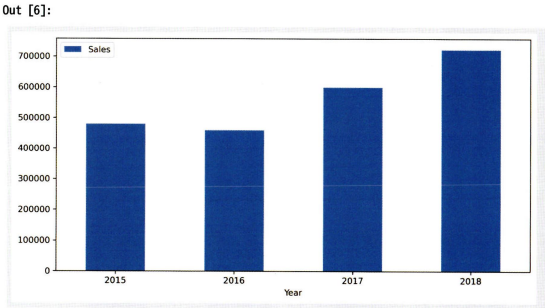
df_bar_1 = df_line.groupby('Year')['Sales'].sum().reset_index()  
ax = df_bar_1.plot.bar(x='Year', y='Sales', rot=0, figsize=(10,5))

image1.png

※ 누적 막대그래프 시각화

1
2
3
4

df_bar_2 = df_line.groupby('Year', 'Segment')['Sales'].sum().reset_index()  

# 고객 세그먼트를 칼럼으로 피벗  
df_bar_2_pv = df_bar_2.pivot(index='Year', columns='Segment', values='Sales').reset_index()

→ 여기까지 데이터 가공 절차

1

df_bar_2_pv.plot.bar(x='Year', stacked=True, figsize=(10,7))

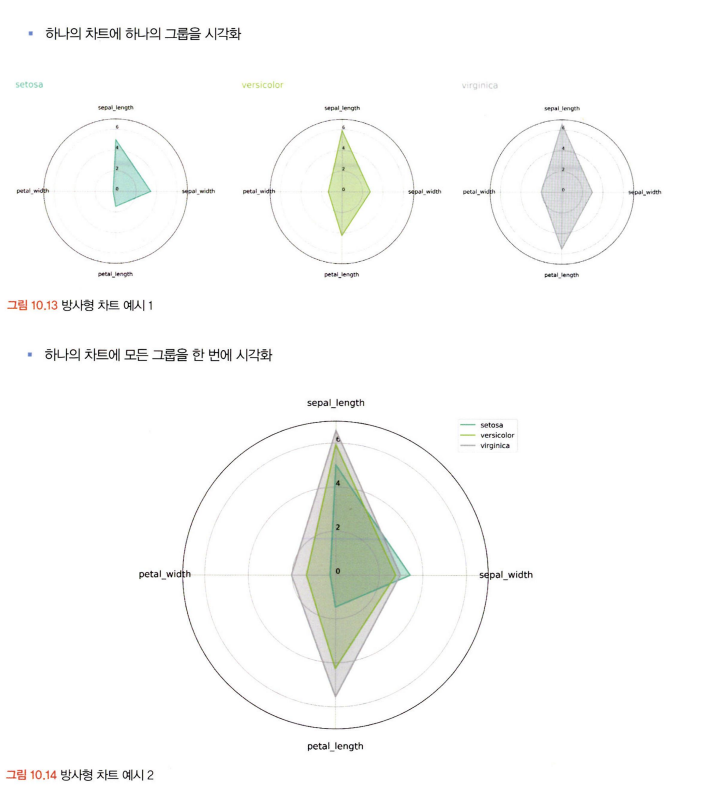
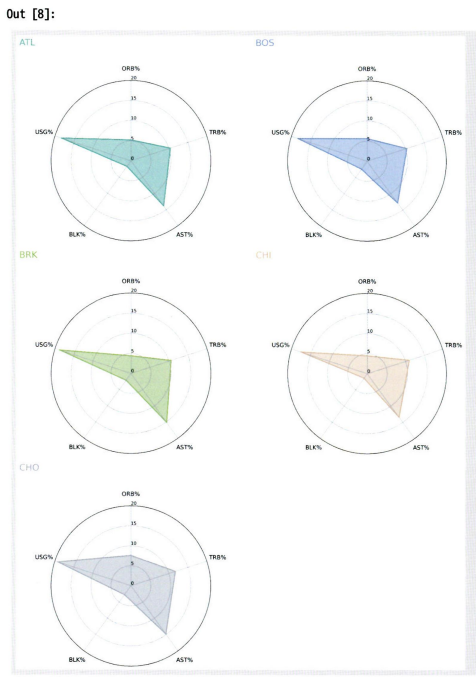
image1.png

10.4 비교 시각화

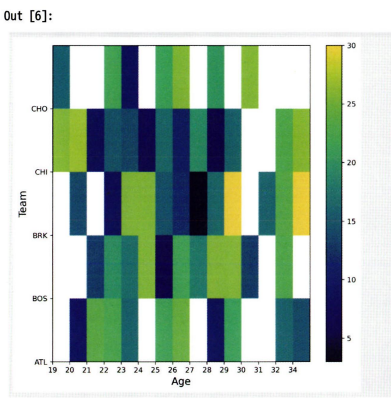
  1. 히트맵 차트
    그룹 별 요소가 많아지게 될 경우 히트맵 차트 방법 사용.
    이를 통해 각 그룹이 어떤 요소에서 높은 혹은 낮은 값을 가지는지 쉽게 파악 가능, 요소 간의 관계 파악 가능.

히트맵 차트 표현 방법

  • 하나의 변수(그룹) * N개의 각 변수에 해당하는 값들(수치형)

  1. 방사능 차트
    image1.png
    image1.png

  2. 평행 좌표 그래프
    image1.png
    평행 좌표 그래프를 보다 효과적으로 표현하기 위해서는 변수별 값 정규화 → 가장 낮은 값은 0, 가장 높은 값은 1로 변환하여 차이를 더욱 부각

10.4.1 비교 시각화 실습

1
2
3
4
5
6
7
8
9
10
11
12
13
14

fig = plt.figure(figure=(8,8))
fig.set_facecolor('white')

plt.pcolor(df2.values)
# x축 칼럼 설정
plt.xticks(range(len(df2.columns)),df2.columns)
# y축 컬럼 설정
plt.yticks(range(len(df2.index)),df2.index)
# x축 레이블 설정
plt.xlable('Age', fontsize=14)
# y축 레이블 설정
plt.ylabel('Team', fontsize=14)
plt.colorbar()
plt.show()

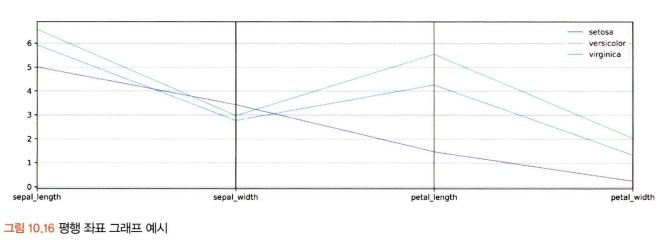
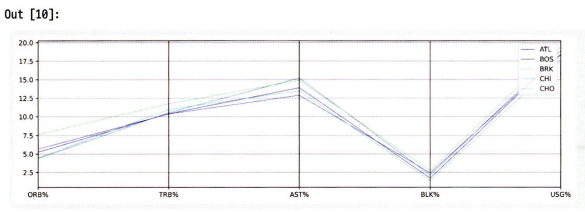
image1.png

※ 방사능 차트 시각화
image1.png
image1.png
image1.png

※ 평행 좌표 그래프 시각화

1
2
3

fig,axes = plt.subplots()
plt.figure(figsize=(6,8))
parallel_coordinates(df3, 'Tm', ax=axes, colormap='winter', linewidth = "0.5")

image1.png

10.5 분포 시각화

분포시각화는 연속형과 같은 양적 척도인지, 명목형과 같은 질적 척도인지에 따라 구분해서 그린다.
막대그래프, 선그래프, 히스토그램 등 활용
각 구간을 bin이라 하며, 구간의 높이는 밀도(density)로 나타낸다.
구간이 너무 많으면 보기 어렵고 너무 적으면 정보 손실이 크기 때문에 적절한 구간 개수가 중요

질적 척도로 이루어진 변수는 구성이 단순한 경우 파이차트나 도넛차트 사용
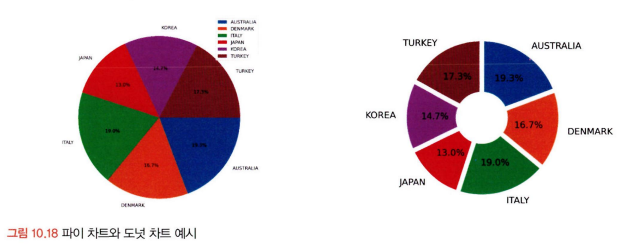
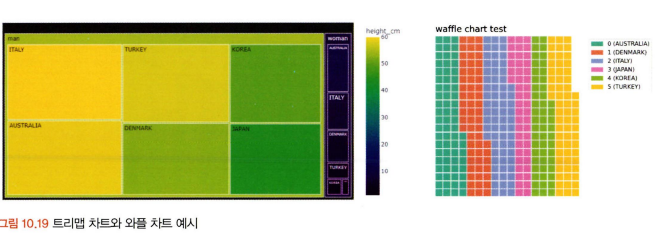
image1.png

구성 요소가 복잡한 질적 척도를 표현할 때는 트리맵 차트가 효율적. But 구성 요소들 간의 규모 차이가 크면 표현이 어려울 수 있음
와플 차트: 트리맵 차트와 유사한 시각화 방법으로 와플처럼 일정한 네모난 조각들로 분포 표현. 하지만 트리맵 차트처럼 위계구조를 표현하지는 못함.

image1.png

10.5.1 분포 시각화 실습

image1.png

※ 기본 히스토그램 시각화

1
2
3
4
5
6
7

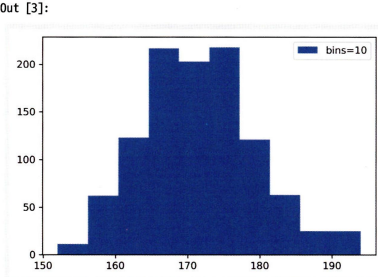
# 신장 칼럼만 필터링 
df1 = df[['height_cm']] 
 
 # 10cm단위로 히스토그램 시각화
 plt.hist(df1, bins=10, label= 'bins=10')
 plt.legend()
 plt.show()

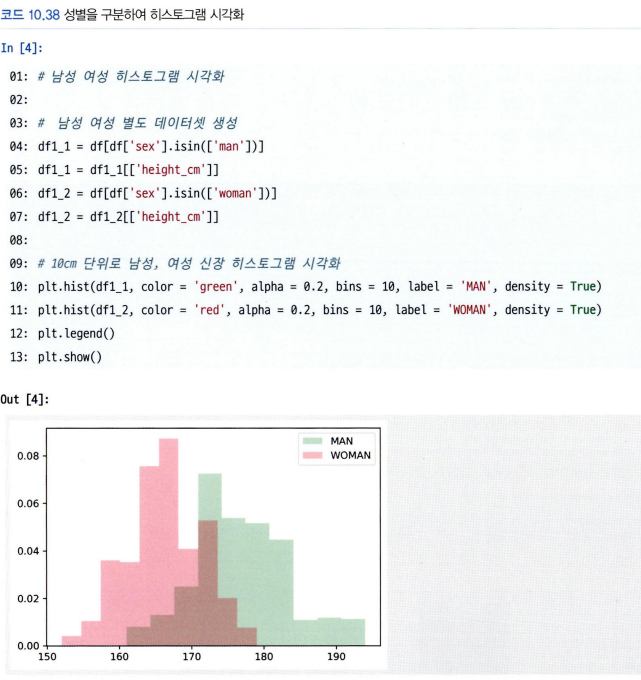
image1.png

image1.png
→ 두 히스토그램 분포가 겹치는 부분을 효과적으로 표현할 수 있음.

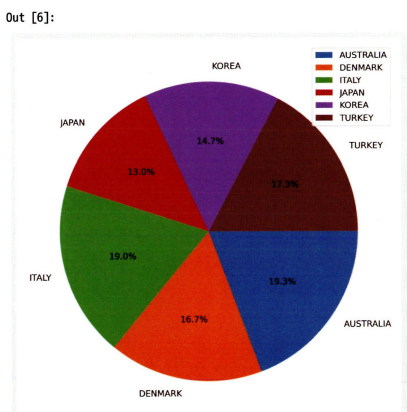
※ 파이차트 시각화

1
2
3
4
5
6
7
8
9
10
11
12
13
14

flg = plt.figure(figsize=(8,8)) # 캔버스 생성
fig.set_facecolor('white') # 캔버스 배경색 설정     
ax=fig.add_subplot() # 프레임 생성

# 파이차트 출력
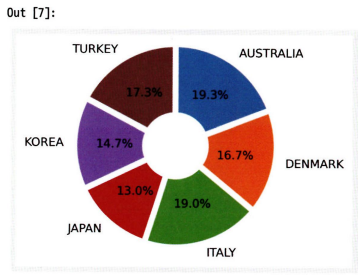
ax.pie(df2.height_cm,
        labels = df2.country,  #라벨 출력
        startangle=0,    # 시작점 degree 설정
        counterclock=False, # 시계방향
        autopct=lambda p : '{:.1f}%'.format(p)  # 퍼센트 자릿수 설정
        )

plt.legend()
plt.show()

image1.png

※ 도넛차트 시각화

1
2
3
4
5
6

wedgeprops = {'width': 0.7, 'edgecolor': 'w', 'linewidth': 5}

plt.pie(df2.height_cm, labels=df2.country, autopct= '%.1f%%',
        startangle=90, counterclock=False, wedgeprops=wedgeprops)

plt.show()

image1.png

※ 트리맵 차트 시각화
image1.png

※ 와플차트 시각화
image1.png

10.6 관계 시각화

  • 두 개의 연속형 변수 간의 관계를 나타낼 수 있는 산점도 활용
    → 산점도를 그릴 때 극단치는 제거하고 그리는게 좋음. 극단치로 인해 주요 분포 구간이 압축되어 시각화의 효율이 떨어지기 때문
  • 산점도는 두개의 변수 간 관계만 표현할 수 있다는 단점이 있음. → 대안으로 버블 차트 활용(두가지 이상의 요소의 상관관계도 표현 가능)
  • 버블 차트는 원의 면적을 함께 봐야하기 때문에 관측치가 너무 많으면 정보전달 효율이 떨어짐.
  • 버블차트를 해석할 때 원의 지름이 아닌 면적으로 크기 판단

10.6.1 관계 시각화 실습

※ 기본 산점도 시각화

1
2

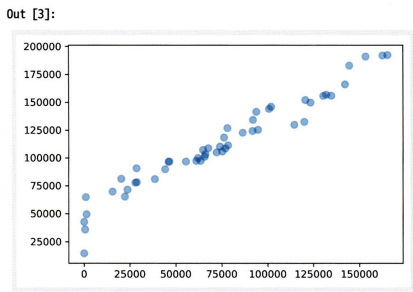
plt.scatter(df['R&D Spend'], df['Profit'], s=50, alpha=0.4)
plt.show()

image1.png

1
2

# 산점도에 회귀선 추가
ax = sns.lmplot(x='R&D Spend', y='Profit', data=df)

※ 버블 차트 시각화

1
2
3

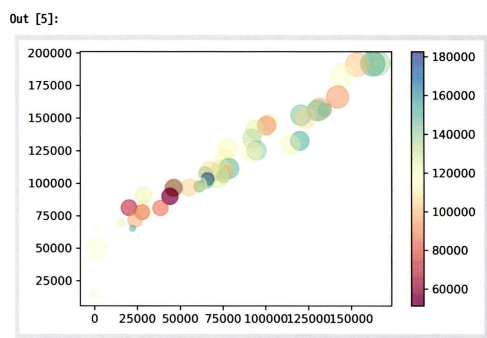
plt.scatter(df['R&D Spend'], df['Profit'], s=df['Marketing Spend']*0.001, c=df['Administration'], alpha=0.5, cmap='Spectral')
plt.colorbar()
plt.show()

image1.png

10.7 공간 시각화

  • 데이터가 지리적 위치와 관련되어 있을 경우에는 지도 위에 데이터 표현이 효율적
  • 위도&경도 데이터를 지도에 매핑하여 시각적으로 표현.(위도&경도 없이도 지도에 위치 표현이 가능한 시각화 프로그램도 있음. ex.GeoMap)
  • 일반적인 사각화 방법과는 달리 지도를 확대하거나 위치를 옮기는 등의 활용 가능.
  • 대표적으로 도트맵, 코로플레스맵, 버블맵, 컨넥션맵 등이 존재
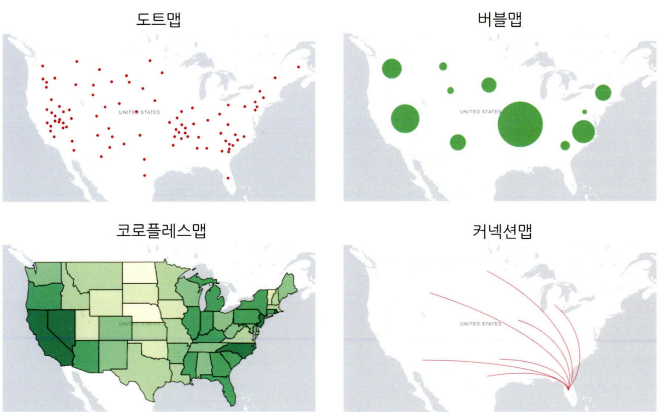
    image1.png

도트맵: 지리적 위치에 동일한 크기의 작은 점을 찍어 해당지역의 데이터 분포나 패턴을 표현하는 기법. 시각적으로 데이터의 개요를 파악하는 데는 유리하지만 정확한 값을 전달하는 데에는 적합하지 않음.

버블맵: 버블차트를 지도에 그대로 옮겨둔 느낌. 하지만 지나치게 큰 버블이 다른 지역의 버블과 겹치면 시각화 효율이 떨어짐.

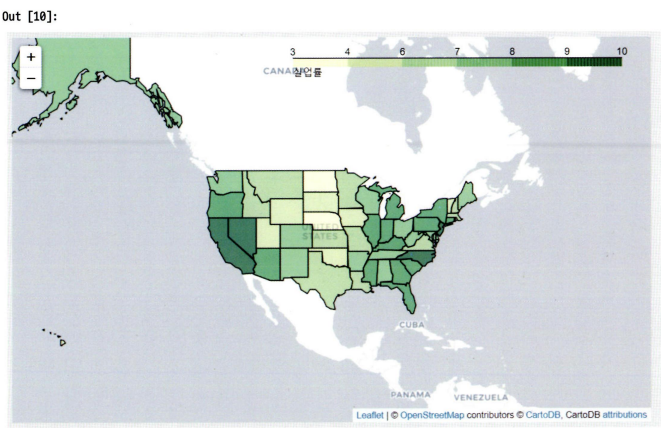
코로플러스맵: 단계 구분도라고도 하며, 데이터 값의 크기에 따라 색상의 음영을 달리하여 해당 지역에 대한 값을 시각화하는 기법. 이 방법 역시 정확한 수치를 인지하고 비교하는 것이 어려움.

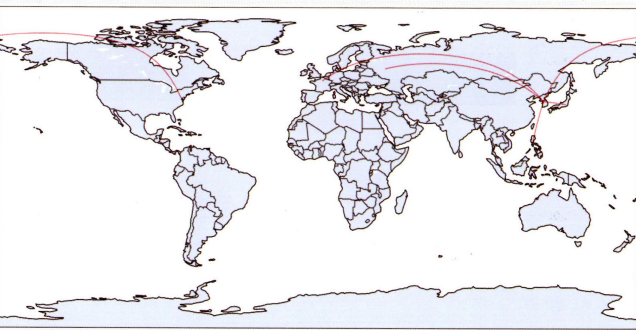
커넥션맵or링크맵: 지도에 찍힌 점들을 곡선 또는 직선으로 연결하여 지리적 관계 표현, 연속적 연결으로 지도에 경로 표현 가능.

플로우맵: 커넥션맵과 유사하게 선을 표현하지만 시작점과 도착점이 함께 표현됨.

카토그램: 각 지역의 면적을 데이터 값에 비례하도록 변형시켜 시각화하는 방법

10.7.1 공간 시각화 실습

※ 기본 지도 시각화

1
2

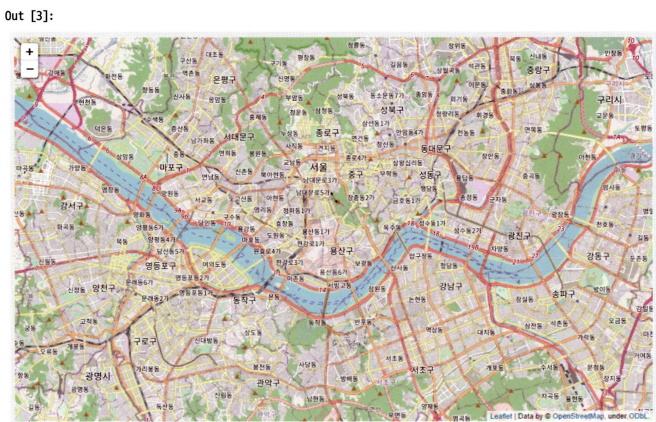
m = foli(location=[37.541,126.986], zoom_start=12)
m

image1.png

1
2
3
4
5
6

# 지도 형태 변경
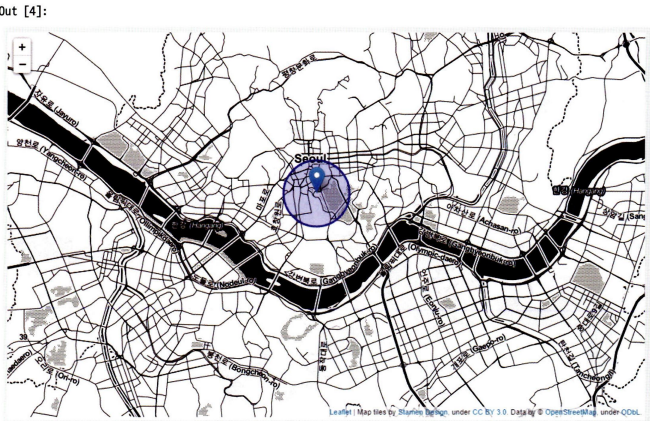
folium.CircleMarker([37.5538, 126.9810], radius=50, popup='Laurelhurst Park', color= '#3246cc', fill_color= '#3246cc').add_to(m)

# 원하는 좌표에 포인트 표시(남산)
folium.Marker([37.5538,126.9810], popup='The Waterfront').add_to(m) 
m

image1.png

※ 군집 마커 시각화

1
2
3
4
5
6
7
8
9

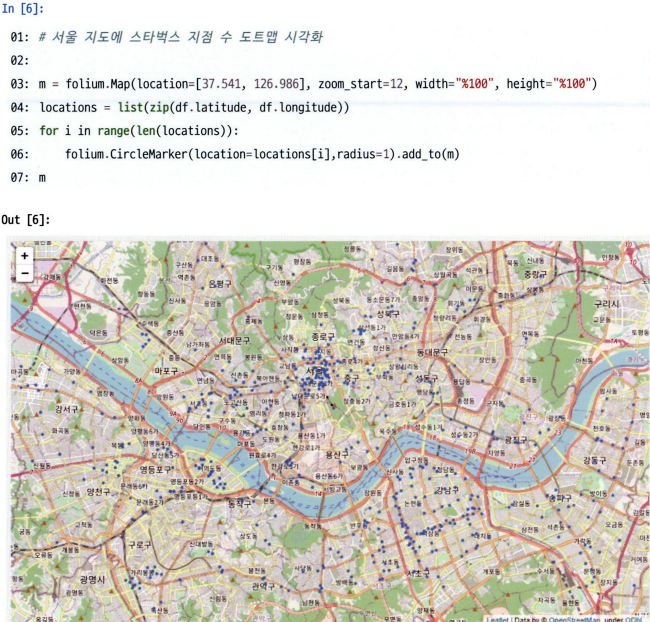
# 서울 지도에 스타벅스 지점 수 시각화  
m = folium.Map([37.541, 126.986], zoom_start=12, width="%100", height="%100")

locations = list(zip(df.latitude, df.longitude))

cluster = plugins.MarkerCluster(locations=locations, popups=df["name"].tolist())

m.add_child(cluster)
m

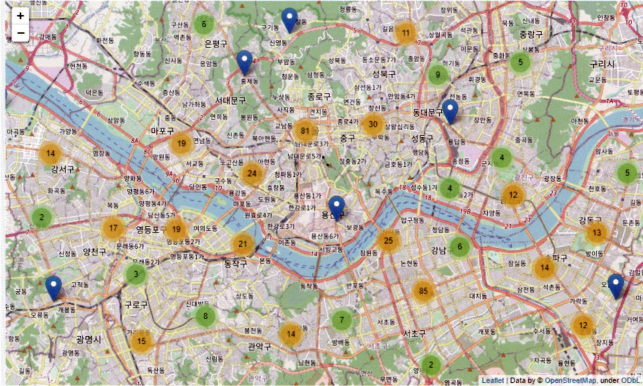
image1.png
MarkerCluster(): 각 구역에 존재하는 스타벅스 지점 수를 숫자로 표현해줌.

※ 도트맵 시각화
image1.png

※ 버블맵 시각화

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

m = folium.Map(location=[37.541, 126.986], tiles='Cartodb Positron', zoom_start=11, width="%100", height="%100")

# 구별 구분선, 색상 설정
folium.Choropleth(
    geo_data=geo,  # 앞에서 불러온 json 파일 적용
    fill_color="gray"
).add_to(m)

# 버블맵 삽입
locations = list(zip(df_m.latitude, df_m.longitude))
for i in range(len(locations)):
    row = df_m.iloc[i]
    folium.CircleMarker(
        location=locations[i],
        radius=float(row['count']) / 2,  # 버블 크기 설정
        fill_color="blue"
    ).add_to(m)

# 지도 출력
m

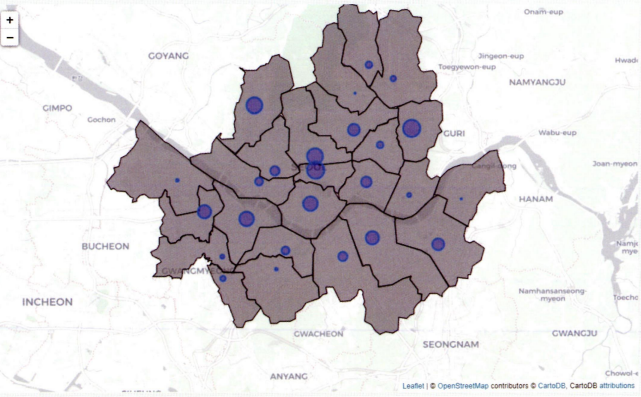
image1.png
CircleMarker()함수로 버블 표현. radius에 매장 수 합계 컬럼 name을 설정하면 매장 수에 따라 버블의 크기가 달라짐. 버블의 크기를 조정하려면 분모 값 조정

※ 코로플레스맵 시각화
image1.png
image1.png

※ 커넥션맵 시각화

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

# 서울과 각국의 수도 간의 커넥션맵 시각화

# 서울과 도쿄, 워싱턴, 마닐라, 파리, 모스크바 위경도 입력
source_to_dest = zip(
    [37.541, 37.541, 37.541, 37.541, 37.541, 37.541],  
    [35.6804, 38.9072, 14.5995, 48.8566, 55.7558],      
    [126.986, 126.986, 126.986, 126.986, 126.986, 126.986],  
    [139.7690, -77.0369, 120.9842, 2.3522, 37.6173]    
)

fig = go.Figure()

## for 문을 활용하여 위경도 입력
for a, b, c, d in source_to_dest:
    fig.add_trace(go.Scattergeo(
        lat = [a, b],
        lon = [c, d],
        mode = 'lines',
        line = dict(width = 1, color="red"),
        opacity = 0.5 # 선 투명도
    ))

fig.update_layout(
    margin={"t":0,"b":0,"l":0,"r":0,"pad":0},
    showlegend=False,
    geo = dict(
        showcountries=True # 국가 경계선
    )
)

fig.show()

image1.png

10.8 박스 플롯

  • 네모 상자 모양에 최댓값과 최솟값을 나타내는 선이 결합된 모양의 데이터 시각화 방법.
  • 박스 플롯은 하나의 그림으로 양적 척도 데이터의 분포 및 편향성, 평균과 중앙값 등 다양한 수치를 보기 쉽게 정리해줌.

박스플롯의 다섯가지 수치

  1. 최솟값: 1사분위에서 1.5IQR을 뺀 위치
  2. 제1사분위: 25%의 위치
  3. 제2사분위: 50%의 위치(중앙값을 의미)
  4. 제3사분위: 75%의 위치
  5. 최댓값: 제3사분위에서 1.5IQR을 더한 위치
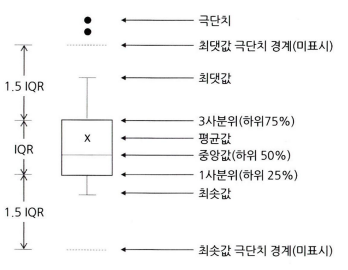
    image1.png
    최댓값or최솟값 극단치 경계를 넘어간 값들은 이상치로 간주. 수염 밖의 점들로 표현
    해당 박스 플롯 구조를 살펴보면 평균보다 중간값이 더 작은 구조를 띄고 있음. → Q. 즉 오른쪽 꼬리가 긴 형태인 Positive Skewness를 가지고 있는데 이를 ‘오른쪽으로 치우친 분포’라고 하는가 ‘왼쪽으로 치우친 분포’라고 하는가? 상식적으로는 분포의 형태가 평균보다 낮은 값의 데이터가 많기에 왼쪽으로 치우친 분포라고 생각하였으나 교과서에는 오른쪽으로 치우친 분포라고 설명하고 있음.

※ 분위수 구하는 수식
image1.png

※ 박스 플롯과 정규분포간의 관계
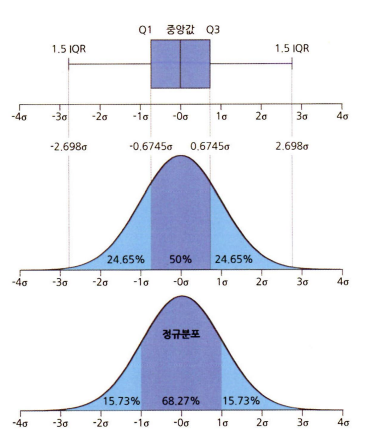
image1.png
박스 플롯을 해석할 때는 항상 데이터 분포도를 함께 떠올리는 습관이 필요함

10.8.1 박스 플롯 실습

※ 기본 박스 플롯 시각화

1
2
3
4
5
6
7
8
9

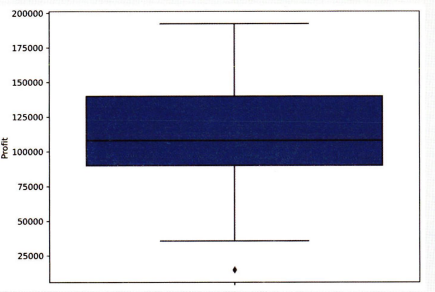
 # 세로 박스 플롯
plt.figure(figsize=(8,6)) 
sns.boxplot(y='Profit', data=df)
plt.show()

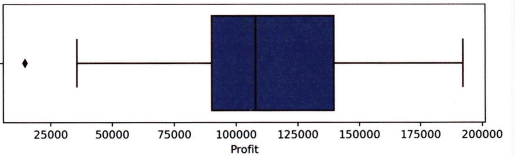
# 가로 박스 플롯
plt.figure(figsize=(8,2))
sns.boxplot(x='Profit', data=df)
plt.show()

image1.png
image1.png

그룹별 박스 플롯 시각화는 위 코드에 x축 설정 추가 (ex. x=”State”)

※ 박스 플롯 추가 옵션 적용

1
2
3
4
5
6

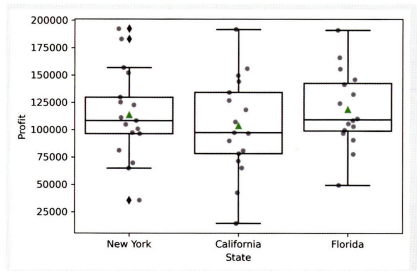
# 평균, 데이터 포인트 포함한 박스 플롯 시각화  
sns.boxplot(x="State", y="Profit", showmeans=True, boxprops={'facecolor':'None'}, data=df)  

sns.stripplot(x='State', y='Profit', data=df, jitter=True, marker='o', alpha=0.5, color='black')

plt.show()

image1.png
평균값 위치와 실제 데이터 포인트 추가 → 이를 통해 분포를 보다 구체적으로 파악할 수 있음.

KHUDA, ML
KHUDA ML
This post is licensed under CC BY 4.0 by the author.

Trending Tags

ML KHUDA Quant FBA_Quant