파이썬으로 구현하는 로보어드바이저 chapter 7. 멀티 팩터 전략
Chapter 7. 멀티 팩터 전략
7.1 팩터로 구하는 국면
어떠한 팩터도 무조건적인 수익을 가져다주는건 없기에 적절한 시기와 전략이 잘 맞는 것이 중요하다.
→ 전략의 수익률을 바탕으로 현재 시장 상황을 정의.
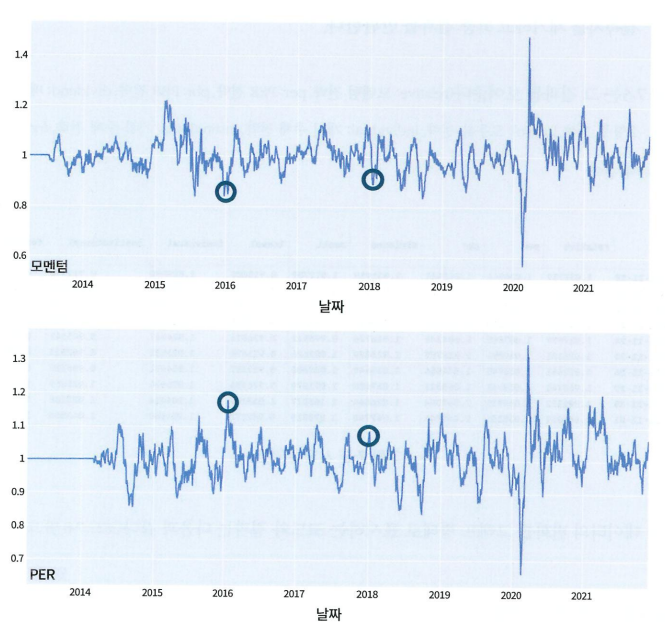
7.1.1 전략별 일별 수익
모멘텀 성과가 잘 나온다 → 시장 호황기
가치주 성과가 잘 나온다 → 기업의 버블이 꺼지는 시기
이런 식으로 각 팩터의 성과를 통해 시장 상황을 파악하고자 한다.
1
target = pd.read_csv('factor_asset.csv', index_col=0)
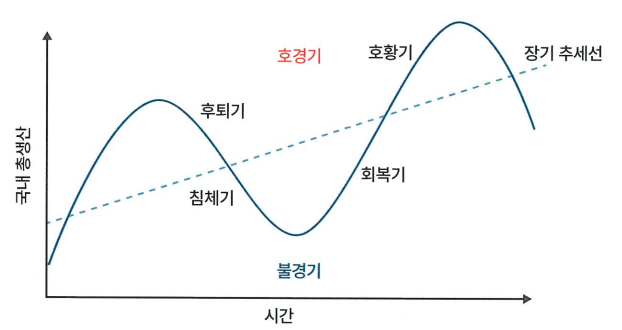
7.1.2 경기 국면과 군집
호황기 → 고성장&고물가, 모멘텀 팩터 강세
후퇴기 → 하락 초기 구간, 물가는 상승
침체기 → 경기&물가 동시 하락. 투자와 생산이 극도로 줄어들고 금리도 낮아진다.
이때는 상대적으로 안정 기업의 부각 현상이 나타나면서 퀄리티 팩터의 활약 가능성이 높음.
회복기 → 기업의 재고가 감소하고 투자, 생산이 늘어남에 따라 경기 상승, 물가 안정, 주가와 금리 상승
이러한 경기 국면을 K-평균 군집화로 분류
이때 일별 수익률의 경우에는 편차가 크기 때문에 시장의 흐름을 판단하기 어렵다. 따라서 일별 수익률이 아닌 월별 수익률을 사용한다.
또한 결과를 추후 예측에 사용해야하기 때문에 사후 데이터를 활용한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def factor_1month_return(df: pd.DataFrame):
# date가 인덱스로 지정되지 않은 데이터에 대한 처리
if 'date' in df.columns:
df = df.set_index('date')
# 일일 변화량 구하기
df = df.pct_change()
# 수익률 곱셈 편의를 위한 +1
df_copy = df.copy()
df_copy = df_copy + 1
# 사후 한 달(21일) 수익률 계산 & 시점 한 달(21일) 전으로 조정
window = df_copy.rolling(21).apply(np.prod, raw=True)
window = window.shift(-21)
return window.dropna()
→ 거래일 21일을 기준으로 함
1
2
3
4
5
6
7
8
9
10
def draw_data_html(df: pd.DataFrame, col: str):
fig = go.Figure()
fig.add_trace(go.Scatter(x=df.index, y=df[col], mode='lines', name='data'))
fig.update_layout(margin=dict(l=20, r=20, t=20, b=60))
fig.add_annotation(dict(font=dict(size=20), x=0, y=0, showarrow=False,
text=f"{eng_to_kor.get(col)}",
textangle=0, xanchor='left', xref="paper",
yref="paper"))
return fig
7.1.3 군집화
K-평균 군집화를 실행하기 위해 최적의 군집 개수를 설정하여야 한다.
이때 군집 내 데이터와 해당 군집의 중심점 간의 거리 제곱합을 나타내는 관성을 측정한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def plot_inertia(df: pd.DataFrame):
# 관성 탐색 범위를 전략 수 만큼 조정
max_k = df.shape[1]
ks = range(1, max_k + 1)
inertias = []
# Cluster 수가 추가됨에 따른 관성 구하기
for k in ks:
model = KMeans(n_clusters=k, n_init='auto')
# K-평균군집화 계산
model.fit(df)
inertias.append(model.inertia_)
plt.plot(ks, inertias, '-o')
plt.xlabel('군집 수 K')
plt.ylabel('관성')
plt.xticks(ks)
plt.show()
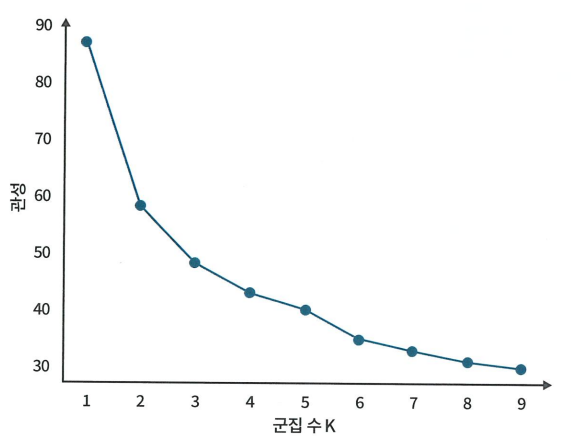
적은 수의 군집으로 충분히 같은 성질을 잘 분류할 수 있는 작은 관성을 갖는 군집 수를 찾는 것이 목표
→ K=3으로 설정
1
2
3
4
5
6
7
8
9
10
11
12
13
def df_with_cluster(df: pd.DataFrame, n_cluster: int, kmeans_model):
df_concern = df.iloc[:, :-1]
# K-평균 군집화 계산
if kmeans_model is None:
kmeans_model = KMeans(n_clusters=n_cluster, n_init='auto')
kmeans_model.fit(df_concern)
# 군집 계산 결과를 기존 데이터프레임에 합체
cluset_result = df_concern.copy()
cluset_result["cluster"] = kmeans_model.labels_
return cluset_result, kmeans_model
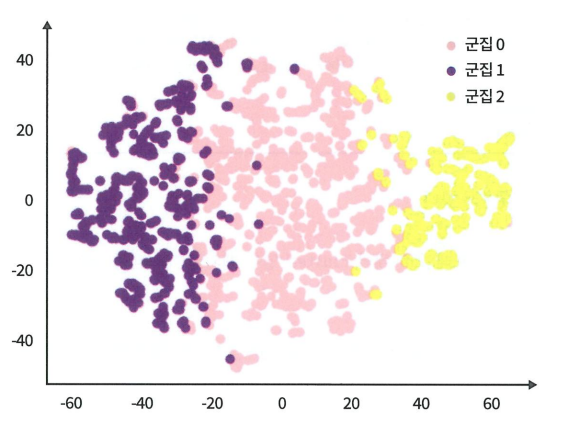
이렇게 군집화를 진행한 후에는 군집 분류 결과를 판단하기 위해 고차원 데이터를 저차원으로 투사해 시각화하는 방법인 t-SNE를 사용한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def check_clustering(df: pd.DataFrame):
# TSNE 기반 차원 축소
tsne = TSNE(n_components=2)
reduced_data = tsne.fit_transform(df.drop(columns='cluster'))
tsne_df = pd.DataFrame(reduced_data, columns=['component_0', 'component_1'])
tsne_df['target'] = df['cluster'].values
# 타깃별 분리
tsne_df_0 = tsne_df[tsne_df['target'] == 0]
tsne_df_1 = tsne_df[tsne_df['target'] == 1]
tsne_df_2 = tsne_df[tsne_df['target'] == 2]
# 타깃별 시각화
plt.scatter(tsne_df_0['component_0'], tsne_df_0['component_1'],
color='pink', label=f'{eng_to_kor.get("cluster")} 0')
plt.scatter(tsne_df_1['component_0'], tsne_df_1['component_1'],
color='purple', label=f'{eng_to_kor.get("cluster")} 1')
plt.scatter(tsne_df_2['component_0'], tsne_df_2['component_1'],
color='yellow', label=f'{eng_to_kor.get("cluster")} 2')
plt.legend()
plt.show()
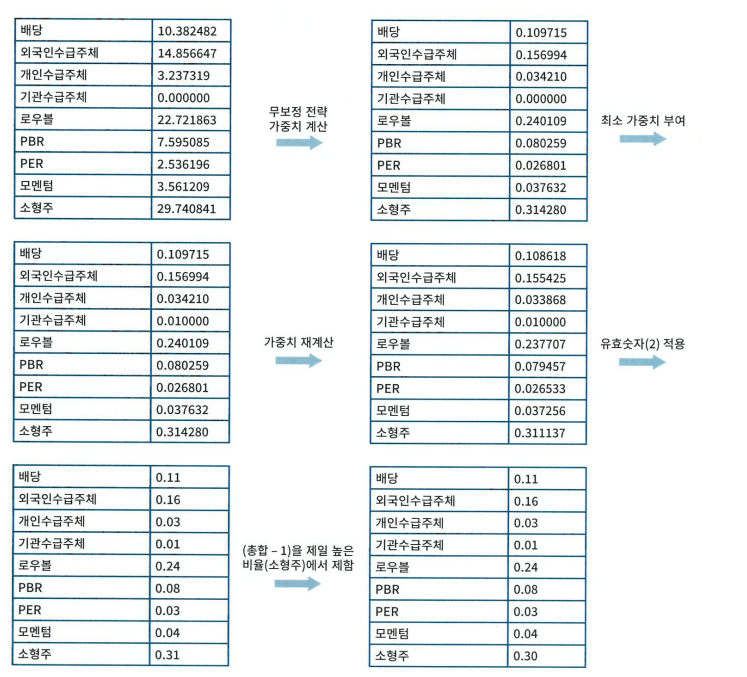
7.1.4 전략 가중치 설정하기
경기 국면별로 각 팩터의 성능을 확인하여 어떤 경기 상황에서 어떤 팩터에 가중치를 많이 주어야 하는지를 알아내고자 한다.
→ 군집별 및 전략별 평균 수익률 확인
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def mean_return_by_cluster(df: pd.DataFrame) -> pd.DataFrame:
return_df = pd.DataFrame(columns=['factor', 'cluster', 'mean_return'])
# 군집 및 전략별 평균 리턴 구하기
for factor in df.columns.drop('cluster'):
factor_data = []
for cycle in sorted(df.cluster.unique()):
mean_value = (df[df.cluster == cycle][factor].mean() - 1) * 100 * 21
factor_data.append(
{'factor': factor, 'cluster': cycle, 'mean_return': mean_value})
return_df = pd.concat([return_df, pd.DataFrame(factor_data)])
return return_df
# 평균 수익률 시각화
def cluster_heatmap(df: pd.DataFrame, var_sort: bool = False):
df = df.rename(columns=eng_to_kor)
# 히트맵을 위한 데이터프레임의 재구조화
pivot_df = df.pivot_table(index=eng_to_kor.get('factor'),
columns=eng_to_kor.get('cluster'),
values='mean_return')
pivot_df = pivot_df.rename(index=eng_to_kor)
# 평균 수익률로 정렬
if var_sort:
pivot_df = pivot_df.sort_values(by=[pivot_df.var().idxmax()])
plt.figure(figsize=(pivot_df.shape[0], int(pivot_df.shape[1]) * 2))
ax = sns.heatmap(pivot_df, xticklabels=True, yticklabels=True)
return ax
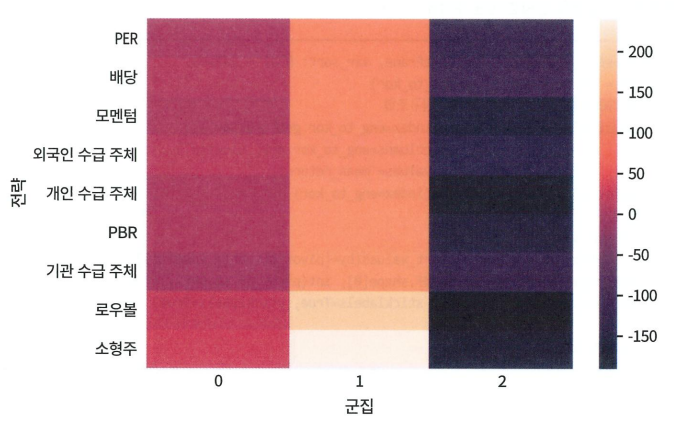
1번 군집의 수익률이 가장 높은 것을 확인할 수 있음. 전체적으로 1번 군집이 상승국면, 2번 군집이 하락국면 형태를 띄고 있다.
2번 군집에서의 배당, 기관 주체 factor는 하락장에서 손실을 최소화하는 성격을 띄고 있다.

→ Q. 최소 가중치가 굳이 필요할까? 왜 있어야 하는걸까
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
def get_strategy_weight(df: pd.DataFrame, min_weight: float) -> pd.DataFrame:
# 데이터프레임의 재구조화
pivot_df = df.pivot_table(index='factor', columns='cluster', values='mean_return')
# 최소 가중치 제약 조건
assert len(pivot_df) <= 1 / min_weight, \
f"min weight too big({min_weight}) for {len(pivot_df)} factors"
# 전체가 음수인 관점의 경우 양수로 바꾸고 약속을 취함
negative_column = pivot_df.columns[(pivot_df < 0).all()]
for column in negative_column:
pivot_df[column] = 1 / -pivot_df[column]
# 음수 제거(0으로 대체)
pivot_df.clip(lower=0, inplace=True)
cluster_variable_pair = defaultdict(list)
# 군집별로 전략 가중치 계산 시작
for cluster in pivot_df.columns:
variables = pivot_df[cluster]
normalized = variables / variables.sum()
normalized.fillna(0, inplace=True)
# 최소한도보다 가중치가 작은 전략이 최소 가중치를 갖게 수정
less_than_min = normalized[normalized < min_weight].index
normalized[less_than_min] = min_weight
# 최소 가중치 전략({less_than_min}) 제외한 나머지 가중치를 다시 전략 가중치 계산
need_adjust = variables.keys().difference(less_than_min.keys())
available_weight = 1 - (min_weight * len(less_than_min))
normalized[need_adjust] = normalized[need_adjust] * available_weight
# 총 요소수 체크점
normalized = normalized.round(2)
# 가중치 재설정 시 생긴 오차를 제로로 가중치를 가진 전략에게 교정
residual = 1 - normalized.sum()
normalized[normalized.argmax()] += residual
cluster_variable_pair[cluster] = normalized
return pd.DataFrame.from_dict(cluster_variable_pair)
7.2 국면 예측
시장을 둘러싼 여러 거시경기 변수가 팩터의 효율과 연관되어있고 경기 상황을 결정짓는다고 볼 수 있다.
→ 금리가 오르면서 장단기 금리차가 상승하면 가치주에 주목할 수 있다. 또한 해외 주식시장 지수가 오르면 국내 시장의 약세를 예측할 수 있다.
7.2.1 거시 경기 데이터
FinanceDataReader 라이브러리, 미국 연방 준비 은행 사이트 등에서 거시경제 데이터들을 불러올 수 있다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
fromdate = '2012-11-01'
todate = '2021-12-30'
macro_name = [
# 주요 지수
'KS200', # 코스피 200
'US500', # S&P 500 지수
'SSEC', # 상해 종합 지수
'VIX', # 변동성 지수
# 상품 선물
'CL', # WTI 서부 텍사스 Crude Oil (NYMEX)
'GC', # 금 선물 (COMEX)
'HG', # 구리 선물 (COMEX)
# 환율
'KRW/USD', # 원달러 환율
'KRW/CNY', # 달러 위안화
# 채권
'US2YT', # 5년 만기 미국국채 수익률
'US10YT', # 10년 만기 미국국채 수익률
'FRED:T10Y3M', # 연준에서 공시하는 10년-3개월 금리차
# 경기 지표(미국)
'FRED:M1SL', # M1 통화량
'FRED:M2SL', # M2 통화량
'FRED:HSN1F', # 미국 HSN1F 주택판매지수
'FRED:TSIFRGHT', # 미국 기타 인플레이션
'FRED:UNRATE', # 미국 실업률
# 경기 지표(한국)
'FRED:NAMNMI01KRM189S', # 대한민국 M1 통화량
'FRED:KORCPIALLMINMEI', # 한국 소비자 물가지수: 모든 항목
'FRED:KORLOCOBXORSTM', # 대한민국 국내총생산: 총규모와 선택사항
'FRED:KORPROINDAISMEI', # 대한민국 생산 지수: 산업 생산
'FRED:KORWRAWRNISMEI', # 대한민국 생산: 수출형 가치
'FRED:XTIMVA01KRM189S', # 대한민국 순수출 가치
]
def macro_data_loader(fromdate, todate, data_list: list) -> pd.DataFrame:
df = pd.DataFrame({'DATE': pd.date_range(start=fromdate, end=todate)})
for data_name in data_list:
# 데이터 로딩
df_sub = find_dataframe(data_name, fromdate, todate)
# OHLCV 중에서 Close만 사용
if 'Close' in df_sub.columns:
df_sub = df_sub[['Close']]
df_sub.rename(columns={'Close': data_name}, inplace=True)
df = df.merge(df_sub, how='left', left_on='DATE', right_index=True)
return df.rename(columns={"DATE": "date"})
1
2
3
4
5
6
7
8
9
# 데이터 전처리
def macro_preprocess(df: pd.DataFrame, fromdate: str, todate: str) -> pd.DataFrame:
# 업무일 데이터로 ffill하기
business_day_list = pd.to_datetime(
PykrxDataloader(fromdate=fromdate, todate=todate).get_business_days()
)
df = df[df['date'].isin(business_day_list)]
return df.ffill().dropna()
→ ffill으로 결측치를 이전 값으로 채워준다.
1
2
3
4
5
6
7
8
9
10
11
12
13
def macro_direction(df: pd.DataFrame, days: int) -> pd.DataFrame:
def _feature_direction(df: pd.DataFrame):
# 선형 회귀 기울기를 구하는 함수 정의
line_fitter = LinearRegression()
fit_result = line_fitter.fit(X=np.arange(len(df)).reshape(-1, 1), y=df)
return fit_result.coef_ / abs(df).mean()
valid_columns = df.columns.drop('date')
# 선형 회귀 계산 윈도우
feature_direction_df = df[valid_columns].rolling(days).apply(_feature_direction)
return feature_direction_df.add_suffix(f'_{days}').ffill()
거시경제 지표의 절대적인 수치 뿐만 아니라 최근 움직임의 정보를 담기 위해 선형회귀를 활용하여 최근 추세 정보를 담는 파생 변수를 만든다.
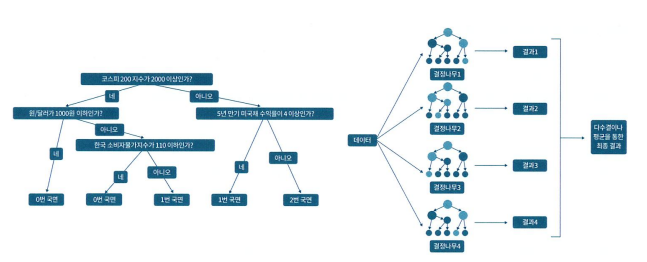
7.2.2 랜덤 포레스트를 통한 군집 예측
좌측의 결정나무를 앙상블하여 구성된 모델이 랜덤 포레스트이며 이때 같은 데이터로만 결정나무들을 학습하면 훈련데이터에 과적합 될 수 있기 때문에 부트스트랩을 활용하여 데이터를 랜덤 샘플링한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
fromdate = '2014-04-01'
todate = '2021-11-30'
def df_within_date(df: pd.DataFrame, fromdate: str, todate: str) -> pd.DataFrame:
if 'date' in df.columns:
df.set_index('date', inplace=True)
return df[fromdate:todate]
def train_RF(train_x: pd.DataFrame, train_y: pd.DataFrame, random_state: int):
train_x_concern = train_x[:-1]
y_train = train_y[['cluster']]
x_train = train_x_concern[:max(y_train.index)]
# 랜덤포레스트 모델 피팅
rf = RandomForestClassifier(n_estimators=50, random_state=random_state)
rf.fit(x_train, y_train.values.ravel())
return rf
→ 2014년 4월 1일부터 2021년 11월 30일까지의 데이터를 train & test 데이터로 사용하여 랜덤 포레스트 모델을 피팅한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
splitdate = '2017-03-31'
def incremental_split(df: pd.DataFrame, split_date: str, loop: int) -> pd.DataFrame:
# 점진 학습을 위한 훈련/예측 데이터 구분점 갱신
split_point = df.index.get_loc(split_date) + loop
return df[:split_point]
# 팩터 가중치 데이터 저장
def get_strategy_weight_per_loop(df: pd.DataFrame, cluster: int, time) -> pd.DataFrame:
single_multifactor = df[cluster].transpose()
single_multifactor['date'] = time.values
return single_multifactor
→ 2017년 3월 31일까지의 데이터를 훈련 데이터로 사용하고 이후 데이터를 예측하는데 활용하게 되면 너무 기간이 멀어질 경우에 오류가 생길수 있다.
따라서 한번에 긴 기간을 예측하지 않고 새로운 데이터가 오면 그것까지 훈련하고 짧은 미래를 예측하는 점진 학습 구조를 취한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
def cluster_weight_prediction(input_df: pd.DataFrame, target_df: pd.DataFrame,
split_start_date: str, n_cluster: int,
min_weight: float,
random_state: Optional[int] = 1) -> tuple:
# 군집 및 전략 가중치/리얼가중치 생성
predictions = np.array([])
reals = np.array([])
real_multifactor = pd.DataFrame()
pred_multifactor = pd.DataFrame()
kmeans_model = None
for loop in tqdm(range(target_df.loc[split_start_date:].shape[0])):
# 점진 학습을 위한 데이터프레임 분할
macro_split = incremental_split(input_df, split_start_date, loop)
target_posterior_split = incremental_split(target_df, split_start_date, loop)
# K-평균 군집화 수행 및 모델 학습
target_posterior_cluster, kmeans_model = df_with_cluster(
df=target_posterior_split,
n_cluster=n_cluster,
kmeans_model=kmeans_model
)
# 거시 경기 데이터를 사용해 랜덤 포레스트 모델 학습
model = train_RF(macro_split, target_posterior_cluster,
random_state=random_state)
# 랜덤 포레스트를 통해 군집 예측 및 실제 군집 저장
pred_cluster = model.predict(macro_split.iloc[-1:])
real_cluster = kmeans_model.predict(target_posterior_split.iloc[-1:])
# 가중치 선택을 위한 팩터 값 원본 평균 수록 및 계산
cluster_return_df = mean_return_by_cluster(target_posterior_cluster)
# 전략 가중치 계산
factor_weight_by_cluster = get_strategy_weight(
df=cluster_return_df,
min_weight=min_weight
)
# 히스토리용 값을 누적 수록
multifactor_time = macro_split.iloc[:-1].index
# 멀티 팩터 정보를 리얼 값과 가정치 저장
pred_row = get_strategy_weight_per_loop(df=factor_weight_by_cluster,
cluster=pred_cluster,
time=multifactor_time)
real_row = get_strategy_weight_per_loop(df=factor_weight_by_cluster,
cluster=real_cluster,
time=multifactor_time)
# 데이터프레임의 통합
predictions = np.append(predictions, pred_cluster)
reals = np.append(reals, real_cluster)
pred_multifactor = pd.concat([pred_multifactor, pred_row])
real_multifactor = pd.concat([real_multifactor, real_row])
return predictions, reals, pred_multifactor, real_multifactor
→ Kmeans로 데이터를 군집화하고 이를 랜덤 포레스트로 예측
7.2.3 예측 평가하기
1
2
3
4
5
6
7
def draw_real_pred_plot(pred: np.array, real: np.array):
plt.figure(figsize=(15, 4))
x = np.arange(0, len(pred), 1)
plt.plot(x, real, label=f'{eng_to_kor.get("real")}')
plt.plot(x, pred, label=f'{eng_to_kor.get("pred")}')
plt.legend()
plt.show()
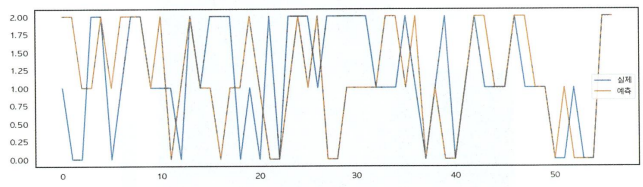
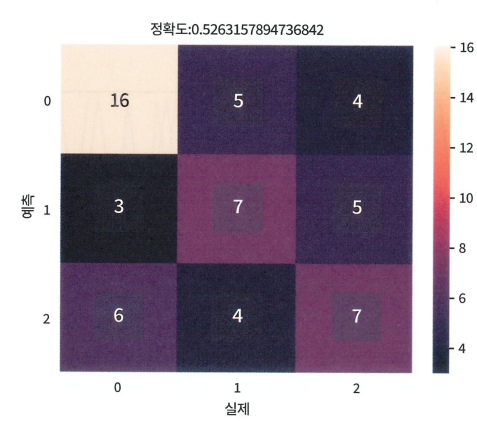
위 그래프로는 직관적으로 예측 성능을 파악하기 어렵기 때문에 분류 결과표 형태로 시각화가 필요함.
1
2
3
4
5
6
7
8
9
10
11
def draw_confusion_heatmap(pred: np.array, real: np.array):
# Scikit-learn의 accuracy_score 사용
accuracy = accuracy_score(pred, real)
plt.figure()
cm = pd.DataFrame(confusion_matrix(pred, real))
ax = sns.heatmap(cm, annot=True)
ax.set(xlabel=f'{eng_to_kor.get("real")}',
ylabel=f'{eng_to_kor.get("pred")}',
title=f'{eng_to_kor.get("accuracy")}: {accuracy}')
plt.show()
1
2
3
4
5
6
7
8
9
10
def draw_factor_weight(df: pd.DataFrame):
df_copy = df.sort_values(by=['date'], ascending=False).copy()
df_copy['date'] = df_copy['date'].dt.strftime("%Y%m")
df_copy.index = df_copy['date']
df_copy.drop(columns=['date'], inplace=True)
sns.set_theme(style='white')
plt.figure(figsize=(df_copy.shape[1] / 2, df_copy.shape[0] / 3))
ax = sns.heatmap(df_copy, xticklabels=True, yticklabels=True)
plt.show()
위 함수에 real_multifactor 변수와 pred_multifactor 변수를 통해 히트맵을 시각화하면 아래와 같다.
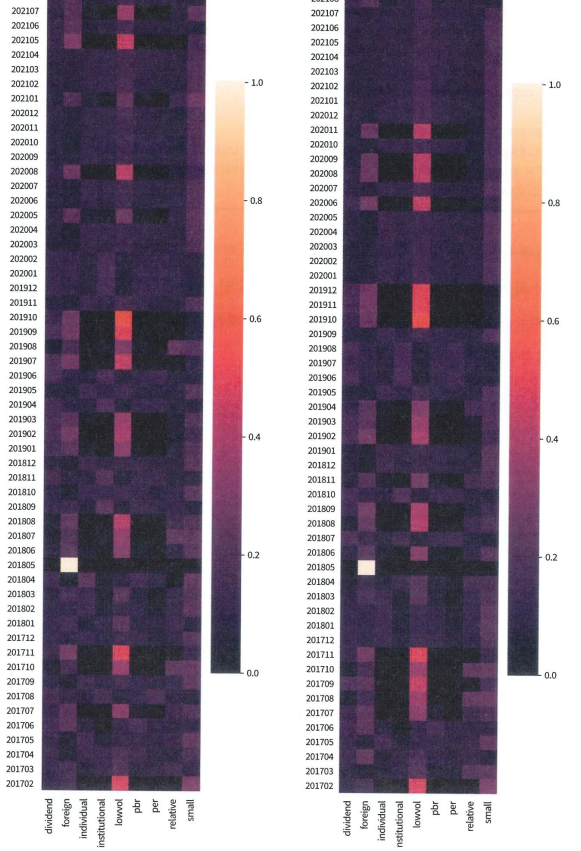
(왼쪽이 실제 결과, 오른쪽이 예측 결과)
대체적으로 두 결과 모두 소형주 전략에 가중치가 높은 편이나 특정 기간에 저변동성 전략의 가중치가 높은 것을 볼 수 있다.
7.3 멀티 팩터 시뮬레이션
7.3.1 포트폴리오 준비
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
# 편입 비중 업데이트
class Account(object):
def __init__(self, initial_cash: float) -> None:
self.weight_history: List[Dict] = []
def update_weight(self, dt: datetime.date, weight: dict):
new_weight = weight.copy()
new_weight['date'] = dt
self.weight_history.append(new_weight)
def simulate_factor(ohlcv_data: pd.DataFrame,
market_cap_data: Optional[pd.DataFrame],
fundamental_data: Optional[pd.DataFrame],
trader_data: Optional[pd.DataFrame],
lookback_period: Optional[int],
skip_period: Optional[int],
strategy_name: str,
buying_ratio: float = 0.1) -> Account:
# 계좌 및 브로커 선언
account = Account(initial_cash=100000000)
broker = Broker()
# 팩터 계산
if strategy_name == "relative":
factor_data = calculate_momentum(ohlcv_data=ohlcv_data,
lookback_period=lookback_period,
skip_period=skip_period)
elif strategy_name in ("per", "pbr"):
factor_data = calculate_fundamental(ohlcv_data=ohlcv_data,
market_cap_data=market_cap_data,
fundamental_data=fundamental_data,
lookback_period=lookback_period,
strategy_name=strategy_name)
elif strategy_name == "small":
factor_data = calculate_small(ohlcv_data=ohlcv_data,
market_cap_data=market_cap_data)
elif strategy_name in ("individual", "institutional", "foreign"):
factor_data = calculate_trader(ohlcv_data=ohlcv_data,
market_cap_data=market_cap_data,
trader_data=trader_data,
lookback_period=lookback_period,
strategy_name=strategy_name)
elif strategy_name == "lowvol":
factor_data = calculate_lowvol(ohlcv_data=ohlcv_data,
lookback_period=lookback_period)
elif strategy_name == "multifactor":
factor_data = calculate_multifactor(ohlcv_data=ohlcv_data)
else:
raise ValueError
# 매월 진행될 날짜 순환
month_end = downsample_ohlcv(ohlcv_data).index
for date, ohlcv in ohlcv_data.groupby('date'):
# 리밸런싱 날짜가 아닐 경우 넘어감
if date not in month_end:
continue
# 포트폴리오 가중치 설정
factor_data_slice = factor_data.loc[date]
weights = get_factor_weight(factor_data=factor_data_slice,
buying_ratio=buying_ratio,
strategy_name=strategy_name)
print(f"Portfolio: {weights}")
if weights is None:
continue
# 포트폴리오 비율 갱신
account.update_weight(dt=date, weight=weights)
return account
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
accounts = defaultdict(list)
portfolios = []
for name, setup in setups.items():
result = simulate_factor(**dict(setup))
accounts[name] = pd.DataFrame(result.account_history)[
['date', 'total_asset']].rename(columns={'total_asset': name})
portfolio = pd.DataFrame(result.weight_history)
portfolio = pd.melt(portfolio, id_vars=['date'], var_name='ticker',
value_name='weight', value_vars=portfolio.columns[1:])
portfolio['factor'] = name
portfolios.append(portfolio)
print(f'strategy made {name}')
factor_portfolio = pd.concat(portfolios).sort_values(
by=['date', 'factor', 'ticker'])
factor_asset = pd.concat(accounts, axis=1)
factor_asset = factor_asset.drop(level=0, axis=1).T.drop_duplicates().T
# Save to CSV
factor_portfolio.to_csv('factor_portfolio.csv')
factor_asset.to_csv('factor_asset.csv')
→ 전략 전체의 편입 비중 csv로 저장
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
# 팩터별 가중치와 포트폴리오 합산
def ticker_weight(factor_weight_df: pd.DataFrame,
portfolio_df: pd.DataFrame) -> pd.DataFrame:
# 비중 테이블 unpivot
weight_melt = pd.melt(factor_weight_df, id_vars=['date'],
value_vars=factor_weight_df.columns[-1:])
weight_melt = weight_melt.sort_values(by=['date', 'factor']).reset_index(drop=True)
# 포트폴리오 테이블 준비
portfolio_df['date'] = pd.to_datetime(portfolio_df['date'])
# 합치기
merged_df = pd.merge(portfolio_df, weight_melt, how='left',
left_on=['date', 'factor'], right_on=['date', 'factor']).dropna()
merged_df['weight'] = merged_df.weight * merged_df.value
merged_df_grouped = merged_df[['date', 'ticker', 'weight']].groupby(
['date', 'ticker']).sum().reset_index()
# 유효숫자 설정
merged_df_grouped.weight = round(merged_df_grouped.weight, 4)
return sum_adjust(merged_df_grouped)
def sum_adjust(df: pd.DataFrame):
# 합쳐서 1이 아닌 가중치 선별 및 차이 계산
df_sum = df.groupby('date').sum()
need_adj = df_sum[~df_sum['weight'].between(0.9, 1)]
need_adj_copy = need_adj.copy()
need_adj_copy['difference'] = need_adj_copy.weight - 1
# 보정
for date, diff in zip(need_adj_copy.index, need_adj_copy.difference):
locator = df[df.date == date]
location = locator[locator.weight > 0].idxmin().weight
df.loc[location, 'weight'] -= diff
return df
→ 보정이 필요할 경우 해당 날짜의 편입 비중이 양수인 가장 작은 값을 찾아서 해당 위치에서 차이만큼을 빼준다.
7.3.2 전략 실행
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def calculate_multifactor(ohlcv_data: pd.DataFrame, oracle: bool = False) -> pd.DataFrame:
# 포트폴리오 CSV 가져오기
filename = 'ticker_weight_real.csv' if oracle else 'ticker_weight_pred.csv'
# 형태 조정
premade = pd.read_csv(filename, index_col=0)
premade.ticker = premade.ticker.astype(str).str.zfill(6)
premade = premade.set_index(['ticker', 'date']).unstack(level=0).weight
premade.index = pd.to_datetime(premade.index)
# 데이터 크기 맞추기
date_pad = downsample_df(ohlcv_data).drop(columns=ohlcv_data.columns)
padded_premade = pd.concat([date_pad, premade])
padded_premade = padded_premade[~padded_premade.index.duplicated(keep='last')]
return padded_premade.sort_index()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def calculate_multifactor(ohlcv_data: pd.DataFrame, oracle: bool = False) -> pd.DataFrame:
# 포트폴리오 CSV 가져오기
filename = 'ticker_weight_real.csv' if oracle else 'ticker_weight_pred.csv'
# 형태 조정
premade = pd.read_csv(filename, index_col=0)
premade.ticker = premade.ticker.astype(str).str.zfill(6)
premade = premade.set_index(['ticker', 'date']).unstack(level=0).weight
premade.index = pd.to_datetime(premade.index)
# 데이터 크기 맞추기
date_pad = downsample_df(ohlcv_data).drop(columns=ohlcv_data.columns)
padded_premade = pd.concat([date_pad, premade])
padded_premade = padded_premade[~padded_premade.index.duplicated(keep='last')]
return padded_premade.sort_index()
→ 멀티 팩터 포트폴리오 준비
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 매수 비율 정의
ratio = 0.1
# 전략 정의
strategy = 'multifactor'
account_multifactor = simulate_factor(
ohlcv_data=df_slicer(df=ohlcv_data_day, fromdate=simulation_fromdate),
market_cap_data=None,
fundamental_data=None,
trader_data=None,
lookback_period=None,
skip_period=None,
strategy_name=strategy,
buying_ratio=ratio
)
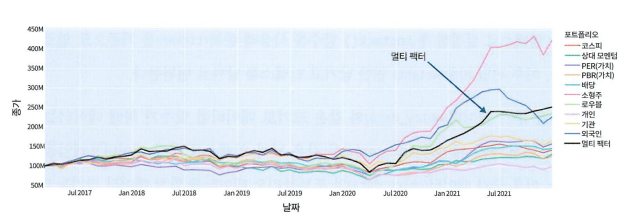
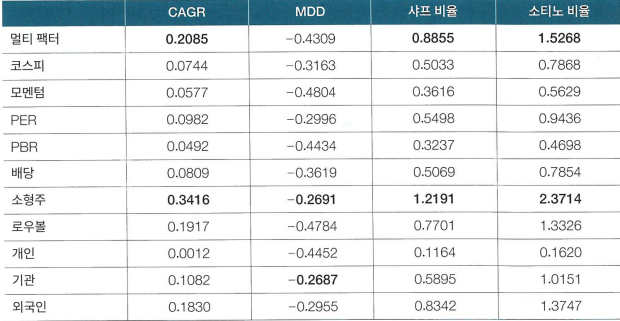
밴치마크 포트폴리오인 KOSPI보다 훨씬 더 좋은 성과를 거둔 것을 볼 수 있다.
눈여겨볼 점은 소형주 전략이 굉장히 높은 성과를 보였다는 것.