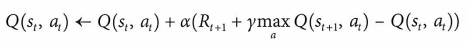금융전략을 위한 머신러닝 chapter 9. 강화 학습 & chapter 10. 자연어 처리

Posted Sep 25, 2024

By AhnHyoungMin

12 min read

Chapter 9. 강화 학습

강화 학습은 보상을 극대화하고 패널티를 최소화하는 최적의 정책을 통해 최선의 조치를 찾도록 머신을 훈련시키는 접근방식이다.

9.1 강화 학습: 이론 및 개념

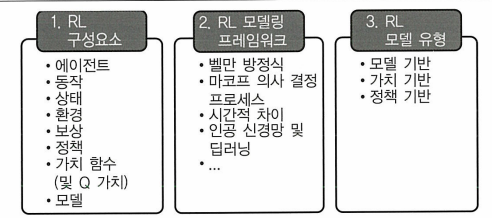
에이전트: 동작을 수행하는 본체
환경: 에이전트가 속해 있는 세계
상태: 현재 상황
보상: 에이전트가 마지막으로 수행한 동작을 평가하기 위해 환경에서 보낸 즉각적인 반환

강화학습의 목표는 실험적 시도와 비교적 간단한 피드백 루프를 통해 최적의 전략을 학습하는 것이다.

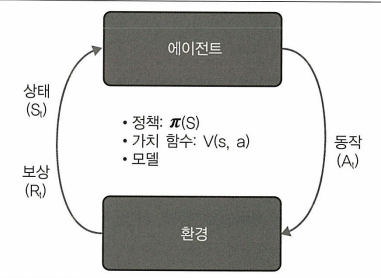
에이전트와 환경 간 상호 작용에는 시간에 따른 일련의 동작과 관찰된 보상이 포함된다. 이 과정에서 에이전트는 환경에 대한 지식을 축적하고 최적의 정책을 학습하며 최상의 정책을 효율적으로 학습하기 위해 이후 조치를 결정한다.

정책: 에이전트가 결정을 내리는 방법을 설명하는 알고리즘 집합이다.
$a_t = \pi(s_i)$
→ 에이전트는 현재 상태에 따라 행동을 결정한다.

가치함수
강화 학습 에이전트의 목표는 환경에서 동작을 잘 수행하는 방법을 학습하는 것이다.
→ 미래 보상 또는 누적 할인 보상 G를 최대화하는 것

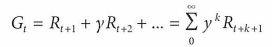
할인 계수 y는 0~1의 값을 가진다.

이때 가치함수는 미래보상 $G_t$의 예측을 통해 상태의 매력도를 측정한다.

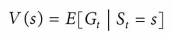
※ 벨만 방정식
벨만 방정식은 가치 함수와 Q가치를 즉각적인 보상과 할인된 미래 가치로 분해하는 방벙식 집합을 나타낸다.

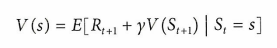
※ 마코프 의사 결정 프로세스
마코프 의사 결정 프로세스(MDP)는 강화 학습 환경을 식으로 설명한다.
S: 상태 집합
A: 일련의 작동
P: 전환 확률
R: 보상 함수
y: 미래 보상에 대한 할인 계수

MDP의 모든 상태에는 미래가 과거가 아니라 오직 현재 상태에 의존한다는 마코프 속성이 있다.

Q 러닝
알고리즘은 Q가치 함수를 기반으로 수행할 동작을 평가하며 Q가치 함수는 특정 상태에서 특정 동작을 수행하는 값을 결정한다.
학습은 비정책 기반으로 진행된다.
1. 시간 단계 t에서는 $s_t$ 상태에서 시작해 Q가치에 따라 동작 $a_t = max_aQ(s,a)$ 를 선택한다.
2. $\epsilon$탐욕 접근방식을 적용해 $\epsilon$확률로 동작을 무작위 선택하거나 Q가치 함수에 따라 최선의 동작을 선택한다. 이것은 주어진 상태에서 새로운 동작의 탐색을 보장하는 동시에 학습 경험을 활용한다.
3. 동작 $a_t$를 취하면 보상 $R_{t+1}$을 확인하고 다음 상태 $S_{t+1}$로 이동한다.
4. 동작-가치 함수를 업데이트한다.
5. 시간 단계를 t=t+1로 증가시키고 단계를 반복한다.

9.4 실전 문제 3: 포트폴리오 배분

이전에 8장의 계층적 위험 패리티(HRP)에서도 설명했던 MVO의 문제점을 해결하기 위해 이번에는 강화학습 관점으로 접근한다.

정책을 스스로 결정할 수 있는 강화 학습 알고리즘은 지속적인 감독 없이 자동화된 방식으로 포트폴리오 배분을 수행할 수 있는 강력한 모델이다.

해당 문제에서는 Q러닝 기반 접근방식과 딥 Q망을 사용하여 일련의 암호화폐 간에 최적의 포트폴리오 배분 정책을 만든다.

문제 정의
- 에이전트
  포트폴리오 매니저, 로보 어드바이저, 개인 투자자

동작
포트폴리오 가중치 할당 및 재조정, 딥 Q망 모델은 포트폴리오 가중치로 변환되는 Q 가치를 제공한다.
보상함수
샤프비율, 수익률 또는 최대 손실률과 같이 수익과 위험 사이의 균형을 제공하는 복잡한 보상 기능이 광범위하게 존재할 수 있다.
상태
상태는 특정 시간 윈도우를 기반으로 한 상품의 상관 행렬이다. 상관 행렬은 서로 다른 상품 간의 관계에 대한 정보가 있고 포트폴리오 배분을 수행하는 데 유용할 수 있으므로 포트폴리오 배분에 적합한 상태 변수이다.
환경
암호화폐 거래소

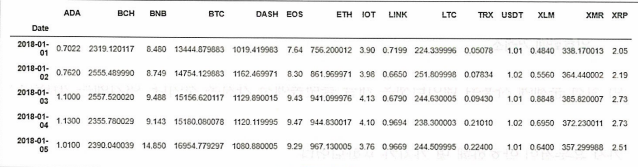
데이터셋은 캐글 플랫폼에서 가져오며 2018년 암호화폐의 일일 가격이 들어있다. 데이터에는 비트코인, 이더리움, 리플, 라이트코인, 대시 등 가장 유동적인 암호화폐 몇 가지가 포함되었다.

시작하기 - 데이터 및 파이썬 패키지 불러오기

  
dataset = read_csv('data/crypto_portfolio.csv', index_col=0)
dataset.head()

알고리즘 및 모델 평가
CryptoEnvironment라는 클래스를 사용해 암호화폐에 대한 시뮬레이션 환경을 구축한다.

getState
is_cov_matrix 또는 is_raw_time_series 플래그에 따라 상태, 과거 수익률, 원시 과거 데이터를 반환한다.
getReward
포트폴리오 가중치와 과거 참조 기간을 고려해 포트폴리오의 보상을 반환한다.

  
class CryptoEnvironment:
    def __init__(self, prices = './data/crypto_portfolio.csv', capital = 1e6):
        self.prices = prices
        self.capital = capital
        self.data = self.load_data()

    def load_data(self):
        data = pd.read_csv(self.prices)
        try:
            data.index = data['Date']
            data = data.drop(columns = ['Date'])
        except:
            data.index = data['date']
            data = data.drop(columns = ['date'])
        return data

    def preprocess_state(self, state):
        return state

    def get_state(self, t, lookback, is_cov_matrix=True, 
                  is_raw_time_series=False):
        assert lookback <= t

        decision_making_state = self.data.iloc[t-lookback:t]
        decision_making_state = decision_making_state.pct_change().dropna()

        if is_cov_matrix:
            x = decision_making_state.cov()
            return x
        else:
            if is_raw_time_series:
                decision_making_state = self.data.iloc[t-lookback:t]
            return self.preprocess_state(decision_making_state)

    def get_reward(self, action, t, reward_t, alpha = 0.81):
        def local_portfolio(returns, weights):
            weights = np.array(weights)
            rets = returns.mean() * 252
            covs = returns.cov() * 252
            P_ret = np.sum(rets * weights)
            P_vol = np.sqrt(np.dot(weights.T, np.dot(covs, weights)))
            P_sharpe = P_ret / P_vol
            return np.array([P_ret, P_vol, P_sharpe])

        data_period = self.data.iloc[:reward_t]
        weights = action
        returns = data_period.pct_change().dropna()
        
        sharpe = local_portfolio(returns, weights)[-1]
        
        sharpe = np.array([sharpe] * len(self.data.columns))
        ret = (data_period.values[-1] - data_period.values[0]) / \
        data_period.values[0]

        return np.dot(returns, weights), ret

  
N_ASSETS = 15
agent = Agent(N_ASSETS)
env = CryptoEnvironment()
window_size = 180
episode_count = 50
batch_size = 32
rebalance_period = 90

Agent 클래스와 CryptoEnvironment 클래스를 초기화한다. 이후 훈련 목적에 맞게 에피소드 수와 배치 크기를 설정한다. 암호화폐의 변동성을 감안하여 window_size는 180으로, rebalancing_frequency는 90일로 설정했다.

데이터 테스트
```python agent.is_eval = True actions_equal, actions_rl = [], [] result_equal, result_rl = [], [] for t in range(window_size, len(env.data), rebalance_period): date1 = t - rebalance_period s_ = env.get_state(t, window_size) action = agent.act(s_)
weighted_returns, reward = env.get_reward(action[0], date1, t) weighted_returns_equal, reward_equal = env.get_reward( np.ones(agent.portfolio_size) / agent.portfolio_size, date1, t )
result_equal.append(weighted_returns_equal.tolist()) actions_equal.append(np.ones(agent.portfolio_size) / agent.portfolio_size)
result_rl.append(weighted_returns.tolist()) actions_rl.append(action[0])

result_equal_vis = [item for sublist in result_equal for item in sublist] result_rl_vis = [item for sublist in result_rl for item in sublist]

plt.figure() plt.plot(np.array(result_equal_vis).cumsum(), label=’Benchmark’, color=’grey’, ls=’–’) plt.plot(np.array(result_rl_vis).cumsum(), label=’Deep RL portfolio’, color=’black’, ls=’-‘) plt.xlabel(‘Time Period’) plt.ylabel(‘Cumulative Return’) plt.show()

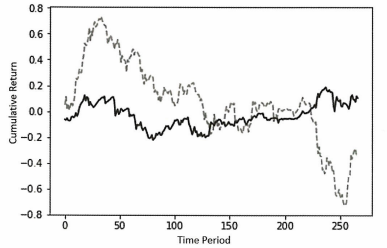
![image1.png](/assets/images/Finance_HW4/image8.png)   
검은색 실선은 포트폴리오의 성능을 나타내며 회색 점선은 동일 가중치 암호화폐 포트폴리오의 성능을 나타낸다.  

초기기간 동안 실적이 저조했지만 주로 테스트 기간의 후반부에 벤치마크 포트폴리오의 성과가 급격히 하락하면서 결과적으로 강화학습 모델 성능이 더 좋게 나왔다. 수익은 매우 안정적으로 보이는데 이는 변동성이 가장 큰 암호화폐에서 벗어나기 때문으로 추정된다.  

```python
import statsmodels.api as sm
from statsmodels import regression

def sharpe(R):
    r = np.diff(R)
    sr = r.mean()/r.std() * np.sqrt(252)
    return sr

def print_stats(result, benchmark):
    sharpe_ratio = sharpe(np.array(result).cumsum())
    returns = np.mean(np.array(result))
    volatility = np.std(np.array(result))

    X = benchmark

    y = result
    x = sm.add_constant(X)
    model = regression.linear_model.OLS(y, x).fit()
    alpha = model.params[0]
    beta = model.params[1]
    
    return np.round(np.array([returns, volatility, sharpe_ratio, alpha, beta]), 4).tolist()

print('EQUAL', print_stats(result_equal_vis, result_equal_vis))
print('RL AGENT', print_stats(result_rl_vis, result_equal_vis))

차례대로 수익률, 변동성, 샤프비율, 알파, 베타이다.
→ 전반적으로 강화 학습 포트폴리오가 높은 수익률, 낮은 수익률, 높은 샤프비율과 양의 알파값을 가지며 벤치마크 포트폴리오와 음의 상관관계를 보이는 것을 알 수 있다.

Chapter 10. 자연어 처리

KHUDA, Finance

This post is licensed under CC BY 4.0 by the author.

Chapter 9. 강화 학습

9.1 강화 학습: 이론 및 개념

9.4 실전 문제 3: 포트폴리오 배분

Chapter 10. 자연어 처리

Trending Tags