금융전략을 위한 머신러닝 chapter 7. 비지도 학습: 차원 축소 & chapter 8. 비지도 학습: 군집화

Chapter 7. 비지도 학습: 차원 축소

7.1 차원 축소 기술

7.1.1 주성분 분석

# PCA 알고리즘 가져오기
from sklearn.decomposition import PCA

# 알고리즘 초기화 및 주성분 수 설정
pca = PCA(n_components=2)

# 데이터에 모델 적합화
pca.fit(data)

# 주성분 리스트 가져오기
print(pca.components_)

# 모델을 데이터로 변환
transformed_data = pca.transform(data)

# 고유값 얻기 (분산 설명 비율)
print(pca.explained_variance_ratio_)

7.1.2 커널 주성분 분석

PCA와는 다르게 커널 주성분 분석(KPCA)는 비선형성을 처리할 수 있다는 장점이 있다.

from sklearn.decomposition import KernelPCA

kpca = KernelPCA(n_components=4, kernel='rbf').fit_transform(X)

7.1.3 t-분산 확률적 이웃 임베딩

각 포인트 주변의 이웃 확률 분포를 모델링해 차원을 줄이는 차원 축소 알고리즘.

from sklearn.manifold import TSNE
X_tsne = TSNE().fit_transform(X)

7.2 실전 문제 1: 포트폴리오 관리(고유 포트폴리오 찾기)

1. 문제 정의
   해당 실전 문제의 목표는 주식 수익 데이터셋에 PCA를 활용하여 주식 포트폴리오의 위험 조정 수익을 극대화 하는 것이다.

다우존스 산업평균지수(DJIA)와 30개 종목이 들어 있는 데이터셋을 사용. 사용된 수익률 데이터는 yfinance에서 2000년 이후 자료를 사용.

1. 시작하기 - 데이터 및 패키지 불러오기

# 차원 축소를 위한 패키지  
from sklearn.decomposition import PCA
from sklearn.decomposition import TruncatedSVD
from numpy.linalg import inv, eig, svd
from sklearn.manifold import TSNE
from sklearn.decomposition import KernelPCA

# 데이터 처리 및 시각화를 위한 패키지
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from pandas import read_csv, set_option
from pandas.plotting import scatter_matrix
import seaborn as sns
from sklearn.preprocessing import StandardScaler

# 데이터 불러오기
dataset = read_csv('Dow_adjcloses.csv', index_col=0)

→ 야후 파이낸스에서 다운받아 다우존스 지수를 구성하는 기업의 조정종가 데이터를 가져온다.

1. 탐색적 데이터 분석

   dataset.shape
   # output: (4804,30)
   

   → 30개 열과 4804개의 행으로 구성.

correlation = dataset.corr()
plt.figure(figsize=(15,15))
plt.title('Correlation Matrix')
sns.heatmap(correlation, vmax=1, square=True, cmap='cubehelix')

일일 수익 간 굉장히 큰 양의 상관관계를 가지는 것을 볼 수 있다.

1. 데이터 준비

# 값 확인 및 제거
print('Null Values =', dataset.insull().values.any())
# output: Null Values = True

missing_fractions = dataset.isnull().mean().sort_values(ascending=False)
missing_fractions.head(10)

drop_list = sorted(list(missing_fractions[missing_fractions > 0.3].index))
dataset.drop(labels=drop_list, axis=1, inplace=True)

dataset.shape
# output: (4804, 20)

→ 적절한 분석을 위해 결측값이 30% 이상인 항목(Dow Chemicals, Visa)은 삭제한다.

# 누락된 값을 데이터셋에서 사용 가능한 마지막 값으로 채우기
dataset=dataset.fillna(method='ffill')

→ ‘Na’는 열의 평균으로 채운다.

PCA를 사용하기 전에 먼저 데이터 스케일링 작업이 필요하다.
해당 작업은 사이킷런의 StandardScaler 함수를 활용할 수 있다.

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler().fit(datareturns)
rescaledDataset = pd.DataFrame(scaler.fit_transform(datareturns), columns =\
    datareturns.columns, index = datareturns.index)
# 변환된 데이터 요약
datareutnrs.dropna(how='any', inplace=True)
rescaledDataset.dropna(how='any', inplace=True)

# DJIA에 대한 로그 수익률 시각화
plt.figure(figsize=(16, 5))
plt.title("AAPL Return")
rescaledDataset.AAPL.plot()
plt.grid(True)
plt.legend()
plt.show()

1. 알고리즘 및 모델 평가
   ```python

   데이터를 훈련셋 및 테스트셋으로 나누기

   percentage = int(len(rescaledDataset) * 0.8) X_train = rescaledDataset[:percentage] X_test = rescaledDataset[percentage:]

stock_tickers = rescaledDataset.columns.values n_tickers = len(stock_tickers)

pca = PCA() PrincipalComponent=pca.fit(X_train)

→ 포트폴리오를 train set과 test set으로 나누고 PCA 수행  

```python
NumEigenvalues = 20

fig, axes = plt.subplots(ncols=2, figsize=(14, 4))
Series1 = pd.Series(pca.explained_variance_ratio_[:NumEigenvalues]).sort_values()
Series2 = pd.Series(pca.explained_variance_ratio_[:NumEigenvalues]).cumsum()

Series1.plot.barh(title='Explained Variance Ratio by Top Factors', ax=axes[0])
Series1.plot(ylim=(0,1), ax=axes[1], title='Cumulative Explained Variance')

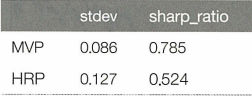
왼쪽 그래프는 각 주성분 별 분산설명력을 나타내는 지표이고 오른쪽 그래프는 누적 분산설명력을 나타내는 그래프이다.

• 주성분0 에서 전체 분산의 약 40%가량을 설명하는 것을 볼 수 있다.
  → 이러한 주성분은 일반적으로 시장 요인으로 해석된다.

def PCWeights():  # 28개 주성분에 대한 가중치
    weights = pd.DataFrame()
    for i in range(len(pca.components_)):
        weights["weights_{}".format(i)] = \
            pca.components_[i] / sum(pca.components_[i])
    weights = weights.values.T
    return weights

weights = PCWeights()
sum(pca.components_[0])
# output: -5.247808242068631

→ 제곱합이 1이 되도록 설정되었기 때문에 합은 1이 되지 않는다. 따라서 각 팩터 로딩값을 가중치로 설정하려면 합이 1이되도록 정규화시켜주어야 한다.

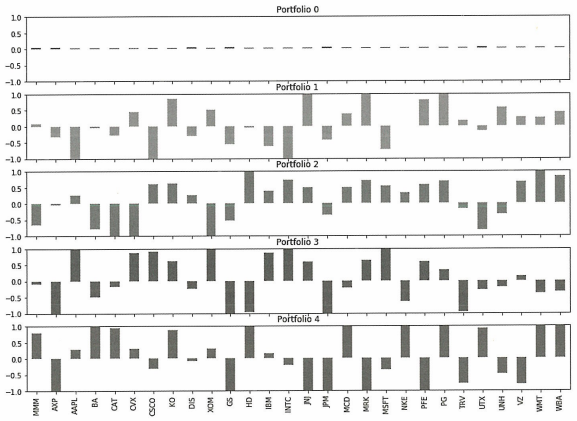
NumComponents = 5
topPortfolios = pd.DataFrame(pca.components_[:NumComponents], \
                             columns=dataset.columns)
eigen_portfolios = topPortfolios.div(topPortfolios.sum(1), axis=0)
eigen_portfolios.index = [f'Portfolio {i}' for i in range(NumComponents)]
np.sqrt(pca.explained_variance_)
eigen_portfolios.T.plot.bar(subplots=True, layout=(int(NumComponents), 1), \
                            figsize=(14, 10), legend=False, sharey=True, ylim=(-1, 1))

분산이 가장 큰 주요 포트폴리오는 일반적으로 systematic risk factor이다. 실제로 주성분0 포트폴리오를 보면 가중치가 종목 전체에 균일하게 분포되어있는 것을 볼 수 있다.  

나머지 포트폴리오는 일반적으로 부문 또는 산업 요소에 해당한다.   

```python
# 샤프 비율 계산
# 연간 거래 일수(즉 252일)를 기준으로 계산
def sharpe_ratio(ts_returns, periods_per_year=252):
    n_years = ts_returns.shape[0] / periods_per_year
    annualized_return = np.power(np.prod(1 + ts_returns), (1 / n_years)) - 1
    annualized_vol = ts_returns.std() * np.sqrt(periods_per_year)
    annualized_sharpe = annualized_return / annualized_vol
    return annualized_return, annualized_vol, annualized_sharpe

def optimizedPortfolio():
    n_portfolios = len(pca.components_)
    annualized_ret = np.array([0.] * n_portfolios)
    sharpe_metric = np.array([0.] * n_portfolios)
    annualized_vol = np.array([0.] * n_portfolios)
    highest_sharpe = 0
    stock_tickers = rescaledDataset.columns.values
    n_tickers = len(stock_tickers)
    pcs = pca.components_

    for i in range(n_portfolios):
        pc_w = pcs[i] / sum(pcs[i])
        eigen_prti = pd.DataFrame(data={'weights': pc_w.squeeze() * 100}, \
                                  index=stock_tickers)
        eigen_prti.sort_values(by=['weights'], ascending=False, inplace=True)
        eigen_prti_returns = np.dot(X_train_raw.loc[:, eigen_prti.index], pc_w)
        eigen_prti_returns = pd.Series(eigen_prti_returns.squeeze(), \
                                       index=X_train_raw.index)
        er, vol, sharpe = sharpe_ratio(eigen_prti_returns)

        annualized_ret[i] = er
        annualized_vol[i] = vol
        sharpe_metric[i] = sharpe

    # 샤프 비율이 가장 높은 포트폴리오 찾기
    highest_sharpe = np.argmax(sharpe_metric)
    print('Eigen portfolio #%d with the highest Sharpe. Return = %.2f%%, \
    vol = %.2f%, Sharpe = %.2f' % 
          (highest_sharpe, 
           annualized_ret[highest_sharpe] * 100,
           annualized_vol[highest_sharpe] * 100,
           sharpe_metric[highest_sharpe]))

    fig, ax = plt.subplots()
    fig.set_size_inches(12, 4)
    ax.plot(sharpe_metric, linewidth=3)
    ax.set_title('Sharpe ratio of eigen-portfolios')
    ax.set_ylabel('Sharpe ratio')
    ax.set_xlabel('Portfolios')

    results = pd.DataFrame(data={'Return': annualized_ret, \
                                 'Vol': annualized_vol, \
                                 'Sharpe': sharpe_metric})
    results.dropna(inplace=True)
    results.sort_values(by=['Sharpe'], ascending=False, inplace=True)
    print(results.head(5))

    plt.show()

optimizedPortfolio()

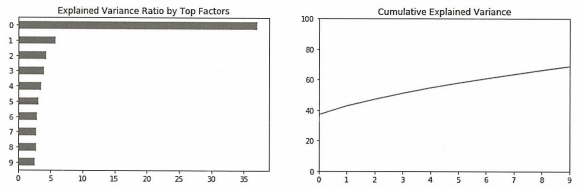
최적의 포트폴리오를 결정하기 위해 각 포트폴리오의 샤프비율을 계산한다.
계산 결과 포트폴리오0의 샤프비율이 0.86으로 가장 높게 측정되었다.

weights = PCWeights()
portfolio = portfolio = pd.DataFrame()

def plotEigen(weights, plot=False, portfolio=portfolio):
    portfolio = pd.DataFrame(data={'weights': weights.squeeze() * 100}, \
                             index=stock_tickers)
    portfolio.sort_values(by=['weights'], ascending=False, inplace=True)
    if plot:
        portfolio.plot(title='Current Eigen-Portfolio Weights',
                       figsize=(12, 6),
                       xticks=range(0, len(stock_tickers), 1),
                       rot=45,
                       linewidth=3
                       )
        plt.show()

    return portfolio

# 가중치는 배열에 저장되며 여기서 0은 첫 번째 주성분의 가중치임.
plotEigen(weights=weights[0], plot=True)

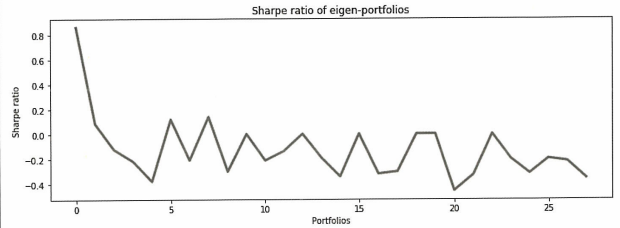
해당 포트폴리오(주성분0)은 전체 데이터 분산의 40%를 설명하기 때문에 risk factor 포트폴리오라고 할 수 있다. 실제로 포트폴리오 가중치 또한 모든 종목의 가중치가 크게 다르지 않다.
다만 금융 부문의 가중치가 더 높은 것으로 보이며 AXP(아메리칸익스프레스), JPM(JP모건 체이스), GS(골드만삭스) 등의 종목이 가중치가 평균 이상인 것을 알 수 있다.

def Backtest(eigen):
    '''
    Plots principal components returns against real returns.
    '''
    eigen_prtfi = pd.DataFrame(data={'weights': eigen.squeeze()}, \
                               index=stock_tickers)
    eigen_prtfi.sort_values(by=['weights'], ascending=False, inplace=True)
    eigen_prtfi_returns = np.dot(X_test_raw.loc[:, eigen_prtfi.index], eigen)
    eigen_portfolio_returns = pd.Series(eigen_prtfi_returns.squeeze(), \
                                        index=X_test_raw.index)
    returns, vol, sharpe = sharpe_ratio(eigen_portfolio_returns)
    print('Current Eigen-Portfolio:\nReturn = %.2f%%\nVolatility = %.2f%%\n\
    Sharpe = %.2f' % (returns * 100, vol * 100, sharpe))

    equal_weight_return = (X_test_raw * (1/len(pca.components_))).sum(axis=1)
    df_plot = pd.DataFrame({'EigenPortfolio Return': eigen_portfolio_returns, \
                            'Equal Weight Index': equal_weight_return}, index=X_test.index)
    np.cumprod(df_plot + 1).plot(title='Returns of the equal weighted\n index vs. First eigen-portfolio', 
                                 figsize=(12, 6), linewidth=3)
    plt.show()

Backtest(eigen=weights[5])
Backtest(eigen=weights[1])
Backtest(eigen=weights[14])

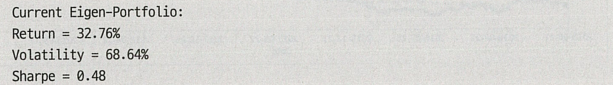
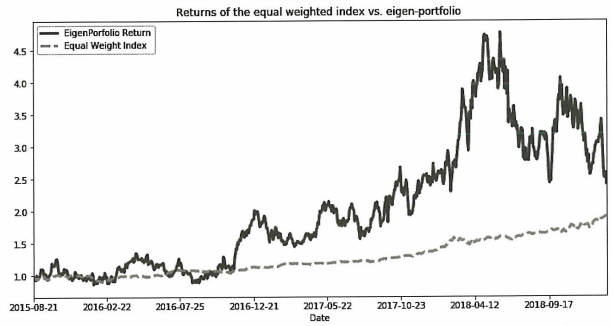
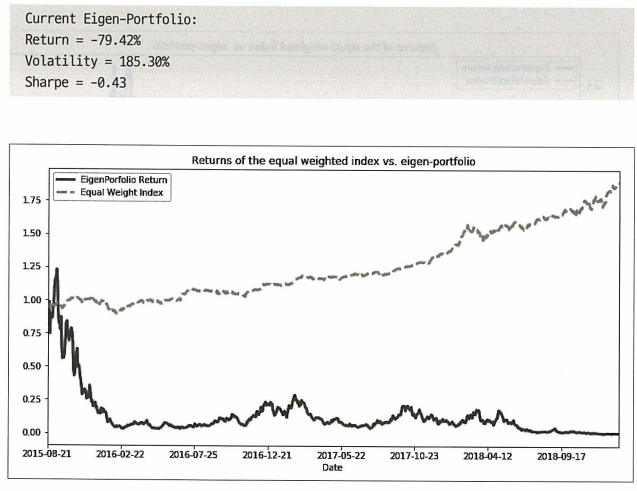
테스트셋으로 알고리즘을 백테스트한 결과 훈련셋에서 상위 성과를 거둔 포트폴리오 5와 1은 각각 0.48, 1.71의 sharpe ratio를 가졌고 하위 성과를 거둔 포트폴리오 14는 -0.43을 가졌다.

이 포트폴리오들은 서로 독립적이라는 점에서 다양화가 가능하다는 장점이 있다. 따라서 상관관계가 없는 포트폴리오에 다방면으로 투자하여 잠재적인 포트폴리오 관리 이점을 얻을 수 있다.

chapter 8. 비지도 학습: 군집화

군집화는 데이터 볼륨을 줄이고 패턴을 찾는 방법이다. 새 변수를 만드는 것이 아닌 원본 데이터를 분류하는 것이다.

8.1 군집화 기술

• k-평균 군집화
• 계층적 군집화
• 선호도 전파 군집화
  해당 챕터에서는 이 3가지 군집화 기술에 대해 다룬다.

8.1.1 k-평균 군집화

k-평균 알고리즘은 데이터 포인트를 찾아서 서로 유사성이 높은 클래스로 그룹화하는 것을 목표로 한다. 데이터 포인트가 서로 가까울수록 동일한 군집에 속할 확률이 높아진다.

알고리즘은 k개의 중심을 찾고 군집 내 분산을 최소화하는 것을 목표로 각 데이터 포인트를 하나의 군집에 할당한다. 일반적으로는 유클리드 거리를 사용하나 다른 거리 측정 방법을 사용할 수 있다.

※ 과정

1. 군집수 지정
2. 군집 중심으로 데이터 포인트를 무작위로 선택
3. 가장 가까운 군집 중심에 데이터 포인트 할당
4. 할당된 포인트의 평균으로 군집 중심 업데이트
5. 모든 군집 중심이 변경되지 않을 때까지 3~4단계 반복

※ k-평균 하이퍼파라미터

• 군집 수
• 최대 반복
• 초기 수

k-평균 알고리즘의 장점은 단순성, 광범위한 적용성, 빠른 수렴, 대용량 데이터에 대한 선형 확장성 등이 있다. 하지만 하이퍼파라미터를 튜닝해야한다는 점과 이상치에 민감하다는 단점이 존재한다.

from sklearn.cluster import KMeans
# k-평균으로 적합화
k_means = KMeans(n_clusters=nclust)
k_means.fit()

8.1.2 계층적 군집화

계층적 군집화는 내림 우선순위가 있는 군집을 생성하는 것이다.
이 기술은 응집 계층적 군집화와 분할 계층적 군집화로 나뉜다.

• 응집 계층적 군집화는 가장 일반적인 계층적 군집화이며 유사성을 기반으로 개체를 그룹화하는 데 사용된다.(바텀업 기반)

※ 과정

1. 각 데이터 포인트를 단일 포인트 군집으로 만들고 N 군집을 형성한다.
2. 가장 가까운 두 데이터 포인트를 가져와 결합해 N-1 군집을 형성한다.
3. 가장 가까운 두 군집을 가져와 결합해 N-2 군집을 형성한다.
4. 군집이 하나만 남을 때까지 3단계 반복

• 분할 계층적 군집화는 모두 N-1 계층적 수준을 생성하고 데이터를 동종 그룹으로 가장 잘 분할하는 수준에서 군집화를 생성한다.(탑 다운 기반)

계층적 군집화를 사용하면 덴드로그램을 그림으로 나타낼 수 있다. 덴드로그램은 서로 다른 데이터셋 간의 계층적 관계를 보여주는 트리 다이어그램의 한 종류를 의미한다.

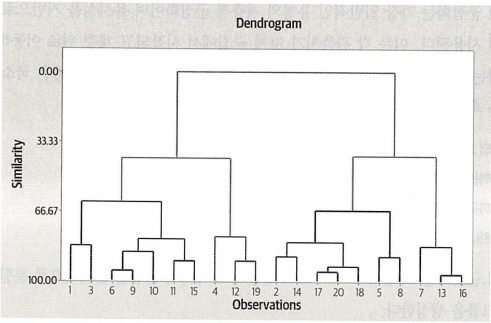
계층적 군집화의 장점은 구현하기 귑고 군집수를 지정할 필요가 없으며 덴드로그램을 통해 데이터를 이해하기 쉽다는 점이다.
반면 시간 복잡성, 이상치에 민감하다는 단점이 존재한다.

from sklearn.cluster import AgglomerativeClustering

# AgglomerativeClustering 객체 생성 (4개의 클러스터로 분류)
model = AgglomerativeClustering(n_clusters=4, affinity='euclidean', linkage='ward')

# 모델을 데이터 X에 맞춰 학습하고 클러스터 라벨을 예측
clust_labels1 = model.fit_predict(X)

8.1.3 선호도 전파 군집화

선호도 전파는 수렴될 때까지 데이터 포인트 간에 메세지를 전송해 군집을 생성한다.

선호도 전파는 군집 수를 결정하기 위해 두 가지 중요한 매개변수를 사용한다.

1. 선호도: 사용되는 예제 수를 제어
2. 감쇠 계수: 메시지의 책임과 가용성을 감소시켜서 메시지를 업데이트할 때 수치적 변동을 피하게 함

적은 수의 예제를 사용하여 데이터셋을 설명하고 이때 예제는 군집을 대표하는 입력셋의 구성원이다.

데이터 포인트 간의 쌍별 유사성 셋을 받아들이고 데이터 포인트와 예제 간의 총합의 유사성을 최대화하여 군집을 찾는다. 이때 쌍 사이에 전송된 메시지는 한 샘플이 다른 샘플에 예제가 될 수 있는 적합성을 나타낸다. 다른 쌍의 값에 응답해 적합성을 업데이트한다. 업데이트는 수렴할 때까지 반복적으로 발생하며 이 과정에서 최종 예제가 선택되고 최종 군집화를 얻는다.

선호도 전파는 초기 군집 수를 설정할 필요가 없고 빠르며 유사성이 큰 행렬에 적용할 수 있다는 장점이 있는 반면 때로는 수렴하지 못할 수 있다는 단점이 있다.

from sklearn.cluster import AffinityPropagation

# 알고리즘 초기화 및 주성분 수 설정
ap = AffinityPropagation()
ap.fit(X)

8.3 실전 문제 2: 포트폴리오 관리(투자자 군집화)

투자 관리자는 투자자의 성향을 분석하고 그에 맞게 전략을 구축해야 하는데 이 과정은 굉장히 많은 시간을 요구한다.
→ 투자자를 유사한 특징을 기반으로 군집화하여 투자자를 위한 맞춤형 관리를 단순화하는 것이 필요하다.

해당 실전 문제에 사용된 데이터는 연방준비제도 이사회에서 실시간 소비자 재정 설문조사에서 가져왔다.

1. 문제 정의
   위험을 감수하려는 능력 및 의지와 관련된 매개변수를 기반으로 투자자를 그룹화하는 군집화 모델을 구축하는 것이 목표

사용하는 설문조사 데이터는 2007년과 2009년 10,000명 이상의 개인 응답과 500개 이상의 특성이 있다. 데이터에 많은 변수가 있기 때문에 먼저 변수 수를 줄이고 투자자의 투자 위험도, 투자 성향과 직접적으로 연결된 가장 직관적인 특성을 선택한다.

1. 시작하기 - 데이터 및 파이썬 패키지 불러오기
   ```python

   군집화 기술을 위한 패키지 가져오기

   from sklearn.cluster import KMeans, AgglomerativeClustering, AffinityPropagation from sklearn.metrics import adjusted_mutual_info_score from sklearn import cluster, covariance, manifold

전처리된 2007년 설문조사용 데이터셋 불러오기

dataset = pd.read_excel(‘ProcessedData.xlsx’)

3. 탐색적 데이터 분석  

```python
dataset.shape
# output: (3866,13)

# 데이터 확인
set_option('display.width', 100)
dataset.head(5)

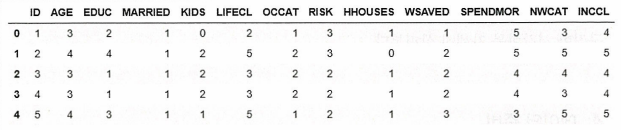
위 표에서 나타난 12개의 속성을 인구 통계, 재무, 행동 속성으로 분류하면 다음과 같다.

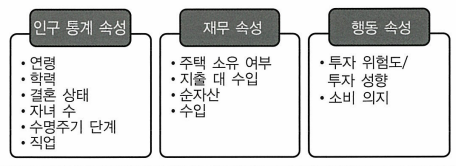
• 수명주기
  위험을 감수하는 능력의 수준을 높이는 여섯가지 범주가 있다. 1은 55세 미만, 미혼, 자녀없음을 나타내고 6은 55세 이상, 일하지 않음을 나타낸다.

• 주택 소유
  1은 개인이 주택을 소유함, 0은 주택을 소유하지 않음을 나타낸다.

• 지출 선호
  자산이 1에서 5까지로 평가될 경우, 지출 선호도가 높음을 나타낸다.

• 연령
  6개의 범주가 있으며 1은 35세 미만, 6은 75세 이상을 나타낸다.

• 학력
  4개의 범주가 있으며 1은 고교 미졸업, 4는 대학 학위를 나타낸다.

• 결혼
  2개의 범주가 있으며 1은 기혼을, 2는 미혼을 나타낸다.

• 직업
  1은 관리 상태를, 4는 실업자를 나타낸다.

• 자녀
  자녀 수를 의미한다.

• 지출 소득
  개인의 지출 대 소득을 나타내며 3개의 범주로 나눈다.

• 순자산
  5개의 범주가 있으며 1은 25번째 백분위수보다 순자산이 적음을 나타내고 5는 90번째 백분위수보다 순자산이 많음을 나타낸다.

• 소득
  5개의 범주가 있으며 1은 천백만원 미만의 소득을, 5는 1억 천만원 이상의 소득을 나타낸다.

• 위험
  위험 감수 의지를 1에서 4까지의 척도로 나타내며 1은 위험을 감수하려는 가장 높은 수준을 나타낸다.

1. 데이터 준비

print('Null Values=', dataset.isnull().values.any())
# output: Null Values = False

→ 누락된 데이터가 없고 데이터가 이미 범주 형식으로 되어있기 때문에 불필요한 ID 열만 삭제한다.

X=X.drop(['ID'], axis=1)

1. 알고리즘 및 모델 평가
   ```python distortions = [] max_loop = 20

for k in range(2, max_loop): kmeans = KMeans(n_clusters=k) kmeans.fit(X) distortions.append(kmeans.inertia_)

fig = plt.figure(figsize=(15, 5)) plt.plot(range(2, max_loop), distortions) plt.xticks([i for i in range(2, max_loop)], rotation=75) plt.grid(True)

![image1.png](/assets/images/Finance_HW3/image16.png)  
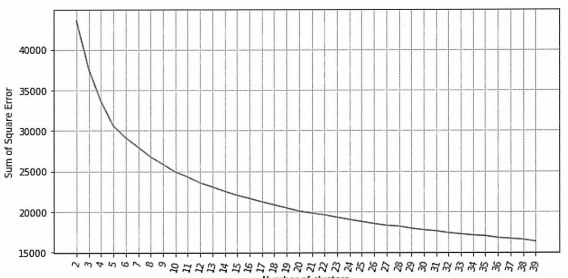
→ 군집 내 SSE를 기준으로 한 엘보우 메소드  

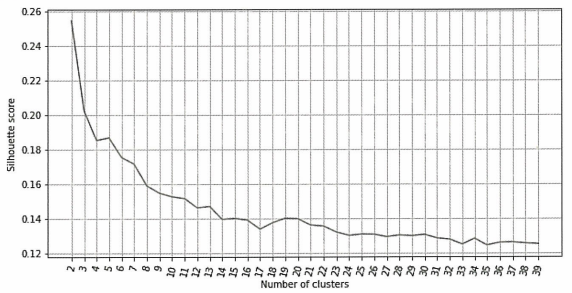
```python
from sklearn import metrics

silhouette_score = []
max_loop = 20

for k in range(2, max_loop):
    kmeans = KMeans(n_clusters=k, random_state=10, n_init=10, n_jobs=-1)
    kmeans.fit(X)
    silhouette_score.append(metrics.silhouette_score(X, kmeans.labels_, random_state=10))

fig = plt.figure(figsize=(15, 5))
plt.plot(range(2, max_loop), silhouette_score)
plt.xticks([i for i in range(2, max_loop)], rotation=75)
plt.grid(True)

→ 실루엣 점수

엘보우 메소드 그래프에서 군집 수가 6개를 넘어가면서 군집 내의 SSE가 정체되고 7개 군집 이후 SSE에 큰 차이가 없으므로 7개 군집을 사용

nclust=7
# k-평균으로의 적합화
k_means = cluster.KMeans(n_clusters=nclust)
k_means.fit(X)

# 레이블 추출
target_labels = k_means.predict(X)

ap = AffinityPropagation()
ap.fit(X)
clust_labels2 = ap.predict(X)
cluster_centers_indices = ap.cluster_centers_indices_
labels = ap.labels_
n_clusters_ = len(cluster_centers_indices)
print('Estimated number of clusters: %d' % n_clusters_)
# output: Estimated number of clusters: 161

→ 선호도 전파 모델을 구축하고 군집 수를 살펴본다. 선호도 전파로 인해 150개가 넘는 군집이 생성되었지만 군집 수가 너무 많다.

from sklearn import metrics
print("km", metrics.silhouette_score(X, k_means.labels_))
print("ap", metrics.silhouette_score(X, ap.labels_))
# output: km 0.170585217843582
#         ap: 0.09736878398868973

k-평균 모델이 선호도 전파에 비해 실루엣 계수가 훨씬 더 높다. 또한 군집 개수도 150개가 넘는 군집보다 6~8개의 군집이 훨씬 실용적이기 때문에 이 문제에서는 k-평균 모델을 사용한다.

1. 군집 직관
   ```python

   클러스터링 결과 출력

   cluster_output = pd.concat([pd.DataFrame(X), pd.DataFrame(k_means.labels_, columns=[‘cluster’])], axis=1) output = cluster_output.groupby(‘cluster’).mean()

인구 통계 특성

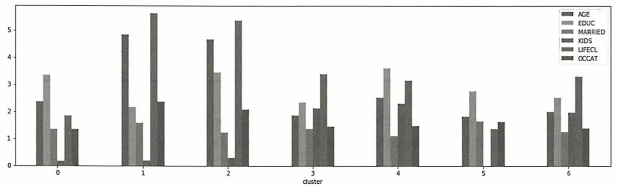
output[[‘AGE’, ‘EDUC’, ‘MARRIED’, ‘KIDS’, ‘LIFECL’, ‘OCCAT’]].plot.bar(rot=0, figsize=(18,5))

![image1.png](/assets/images/Finance_HW3/image18.png)  

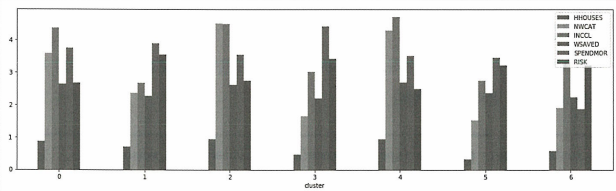
```python
# 재무 및 행동 속성
output[['HHOUSES', 'NWCAT', 'INCCL', 'WSAVED', 'SPENDMOR', 'RISK']].plot.bar(rot=0, figsize=(18,5))

위 차트들은 각 군집에 대한 인구 통계, 재무 및 행동 속성의 평균값을 보여준다.

이렇게 군집화 알고리즘을 활용하여 투자자의 다양한 특성을 기준으로 그룹화하여 각 군집이 가지는 위험 대처 능력을 효율적으로 나타낼 수 있다.

8.4 실전 문제 3: 계층적 위험 패리티

해리 마코위츠의 MVO는 포트폴리오 구성 및 자산 배분에 가장 일반적으로 사용되는 기술이지만 공분산 행렬과 기대수익률을 추정하는 과정에서 추정오류로 인한 문제가 크기 때문에 실용적이지 못하다는 단점이 존재한다.
→ 마르코 로페즈 드 프라노는 계층적 리스크 패리티라는 군집화를 기반으로 한 포트폴리오 배분 방법을 제안한다.

• 계층적 리스크 패리티의 주요 아이디어는 주식 수익의 공분산 행렬에서 계층적 군집화를 실행한 다음 각 군집 계층에 자본을 균등하게 분배하여 다양한 가중치를 찾는 것이다.
  → 마코위츠의 MVO에서 발견된 문제를 완화하고 수치 안정성을 향상시킬 수 있다.

이 실전 문제에 사용된 데이터셋은 2018년부터 S&P500 주식의 가격 데이터이다.

1. 문제 정의
   주식 데이터셋에서 군집화 기반 알고리즘을 사용해 자본을 서로 다른 자산 클래스에 배분하는 것이 목표.
   포트폴리오 배분을 MVO와 백테스트하고 비교하기 위해 시각화를 수행하고 샤프비율로 성능 평가

2. 시작하기 - 데이터 및 파이썬 패키지 불러오기
   ```python

   모델 패키지 불러오기

   import scipy.cluster.hierarchy as sch from sklearn.cluster import AgglomerativeClustering from scipy.cluster.hierarchy import fcluster from scipy.cluster.hierarchy import dendrogram, linkage, cophenet from sklearn.metrics import adjusted_mutual_info_score from sklearn import cluster, covariance, manifold import ffn

평균 분산 최적화를 위한 패키지

import cvxopt as opt from cvxopt import blas, solvers

```python
dataset = read_csv('SP500Data.csv', index_col=0)

# 형태
dataset.shape
# output: (448,502)

1. 데이터 준비

# null값 확인 및 제거
print('Null Values =', dataset.isnull().values.any())
# output: Null Values = True

→ 결측치가 존재하므로 제거해주어야 한다.

missing_fractions = dataset.isnull().mean().sort_values(ascending=False)
missing_fractions.head(10)
drop_list = sorted(list(missing_fractions[missing_fractions > 0.3].index))
dataset.drop(labels=drop_list, axis=1, inplace=True)
dataset.shape
# output: (448,498)

# 누락된 값을 데이터셋에서 사용 가능한 마지막 값으로 채움
dataset=dataset.fillna(method='ffill')

X = dataset.copy('deep')
row = len(X)
train_len = int(row * 0.8)
X_train = X.head(train_len)
X_test = X.tail(row - train_len)

# 수익률 계산
returns = X_train.to_returns().dropna()
returns_test = X_test.to_returns().dropna()

군집화에 연간 수익을 사용하고 테스트셋으로 20%를 사용한다.

1. 알고리즘 및 모델 평가
   먼저 응집 계층적 군집화 기술을 사용하여 상관관계 군집을 찾는다.
   계층 구조 클래스에는 동일한 클래스의 연결 메서드에서 반환된 값을 사용하는 덴드로그램 메서드가 있다. 연결 방법은 데이터셋과 메서드를 매개변수로 사용하여 거리를 최소화하는 것인데 이때 거리 측정 방법으로 군집 사이의 거리 분산을 최소화하는 와드를 선택한다.

Z = [stock_1, stock_2, distance, sample_count]

def correlDist(corr):
    # 상관관계를 기반으로 하는 거리 행렬, 여기서 <= d[i,j] <= 1
    # 적절한 거리 측정법임
    dist = ((1-corr) / 2.) ** .5
    # 거리 행렬
    return dist

# 연결 계산
dist = correlDist(returns.corr())
link = linkage(dist, 'ward')
# 덴드로그램 그리기
plt.figure(figsize=(20, 7))
plt.title("Dendrograms")
dendrogram(link, labels=X.columns)
plt.show()

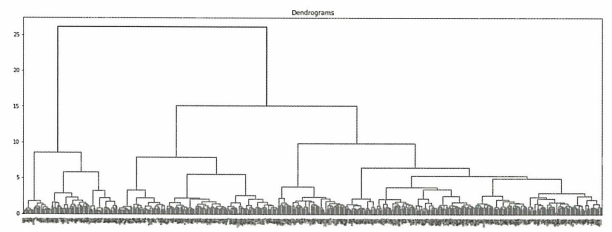
이 차트에서 가로축은 군집을 나타내며 적절한 군집 수는 2 or 3 or 6으로 나타난다.

계층적 위험 패리티(HRP) 알고리즘은 세 단계로 작동한다.

• 트리 군집화
  상관 행렬을 기반으로 유사한 투자를 군집으로 그룹화한다. 계층 구조가 있는 것은 공분산 행렬을 역으로 변환할 때 2차 최적화의 안정성 문제를 개선하는 데 도움이 된다.

• 준대각화
  유사한 투자가 함께 배치되도록 공분산 행렬을 재구성한다. 행렬 대각화를 통해 역분산 할당에 따라 가중치를 최적으로 분배할 수 있다.

• 재귀 이분법
  군집 공분산을 기반으로 재귀적 이분법을 통해 배분한다.

※ 준대각화

def getQuasiDiag(link):
    # 거리별로 군집화된 항목 정렬
    link = link.astype(int)
    sortIx = pd.Series([link[-1, 0], link[-1, 1]])
    numItems = link[-1, 3] # 원래 항목 수
    while sortIx.max() > numItems:
        sortIx.index = range(0, sortIx.shape[0] * 2, 2) # 공간 생성
        df0 = sortIx[sortIx >= numItems] # 군집 찾기
        i = df0.index
        j = df0.values - numItems
        sortIx[i] = link[j, 0] # 항목 1
        df0 = pd.Series(link[j, 1], index=i + 1)
        sortIx = sortIx.append(df0) # 항목 2
        sortIx = sortIx.sort_index() # 재정렬
        sortIx.index = range(sortIx.shape[0]) # 재색인
    return sortIx.tolist()

유사한 투자를 함께 배치하도록 공분산 행렬을 재구성한다. 이 행렬 대각화를 통해 역분산 할당에 따라 가중치를 최적으로 분배할 수 있다.

※ 재귀 이분법

def getIVP(cov, **kargs):
    # 역분산 포트폴리오 계산
    ivp = 1. / np.diag(cov)
    ivp = ivp / sum(ivp)
    return ivp

def getClusterVar(cov, cItems):
    # 군집당 분산 계산
    cov_ = cov.loc[cItems, cItems] # 행렬 분할
    w_ = getIVP(cov_).reshape(-1, 1)
    cVar = np.dot(np.dot(w_.T, cov_), w_)[0, 0]
    return cVar

def getRecBipart(cov, sortIx):
    # HRP 배분 계산
    w = pd.Series(1, index=sortIx)
    cItems = [sortIx] # 하나의 군집에서 모든 항목 초기화
    while len(cItems) > 0:
        cItems = [i[j:k] for i in cItems for j, k in ((0, len(i) // 2), (len(i) // 2, len(i)))] # 이동분할
        for i in range(0, len(cItems), 2): # 쌍으로 구문 분석
            cItems0 = cItems[i] # 군집 1
            cItems1 = cItems[i + 1] # 군집 2
            cVar0 = getClusterVar(cov, cItems0)
            cVar1 = getClusterVar(cov, cItems1)
            alpha = 1 - cVar0 / (cVar0 + cVar1)
            w[cItems0] *= alpha # 가중치 1
            w[cItems1] *= 1 - alpha # 가중치 2
    return w

getVIP 함수로 역분산 포트폴리오를 정의하고 getClusterVar 함수에서 군집 분산을 계산하며 getRecBipart 함수로 군집 공분산을 기반으로 하는 재귀 이분법을 통해 최종 배분을 계산한다.

def getHRP(cov, corr):
    # 계층적 포트폴리오 구성
    dist = correlDist(corr)
    link = sch.linkage(dist, 'single')
    #plt.figure(figsize=(20, 10))
    #dn = sch.dendrogram(link, labels=cov.index.values)
    #plt.show()
    
    sortIx = getQuasiDiag(link)
    sortIx = corr.index[sortIx].tolist()
    hrp = getRecBipart(cov, sortIx)
    return hrp.sort_index()

→ 군집화, 준대각화, 재귀 이분법의 세 단계를 결합하여 최종 가중치를 생성한다.

def getMVP(cov):
    cov = cov.T.values
    n = len(cov)
    N = 100
    mus = [10 ** (5.0 * t / N - 1.0) for t in range(N)]
    
    # cvxopt 행렬로 변환
    S = opt.matrix(cov)
    pbar = opt.matrix(np.mean(returns, axis=1))
    pbar = opt.matrix(np.ones(cov.shape[0]))
    
    # 제약 행렬 만들기
    G = -opt.matrix(np.eye(n))  # 음의 n x n 단위 행렬
    h = opt.matrix(0.0, (n, 1))
    A = opt.matrix(1.0, (1, n))
    b = opt.matrix(1.0)
    
    # 2차 계획법을 사용해 효율적인 프론티어 가중치 계산
    solvers.options['show_progress'] = False
    portfolios = [solvers.qp(mu * S, -pbar, G, h, A, b)['x'] for mu in mus]
    
    # 포트폴리오의 위험과 수익 계산
    returns = [blas.dot(pbar, x) for x in portfolios]
    risks = [np.sqrt(blas.dot(x, S * x)) for x in portfolios]
    
    # 포트폴리오 곡선의 2차 다항식 계산
    m1 = np.polyfit(returns, risks, 2)
    x1 = np.sqrt(m1[2] / m1[0])
    
    # 최적의 포트폴리오 계산
    wt = solvers.qp(opt.matrix(x1 * S), -pbar, G, h, A, b)['x']
    return list(wt)

→ 마코위츠의 MVO를 기반으로 포트폴리오 배분을 계산하는 MVP함수를 정의한다.

def get_all_portfolios(returns):
    cov, corr = returns.cov(), returns.corr()
    hrp = getHRP(cov, corr)
    mvp = getMVP(cov)
    mvp = pd.Series(mvp, index=cov.index)
    portfolios = pd.DataFrame([mvp, hrp], index=['MVP', 'HRP']).T
    return portfolios

# 포트폴리오를 얻고 원그래프 그리기
portfolios = get_all_portfolios(returns)
portfolios.plot.pie(subplots=True, figsize=(20, 10), legend=False)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(30, 20))
ax1.pie(portfolios.iloc[:, 0])
ax1.set_title('MVP', fontsize=30)
ax2.pie(portfolios.iloc[:, 1])
ax2.set_title('HRP', fontsize=30)

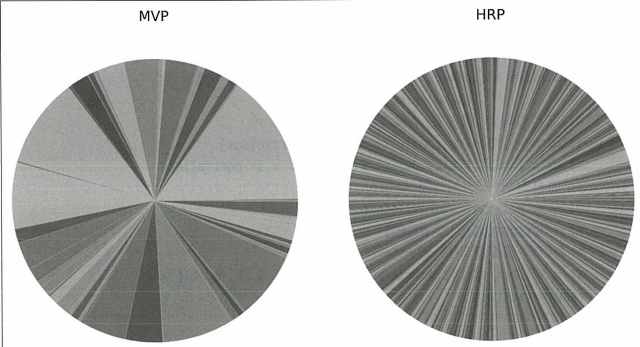
각 포트폴리오의 가중치를 파이 차트로 시각화하여, 두 포트폴리오 간 자산 배분의 차이를 시각적으로 비교한 결과 HRP이 더 잘 다각화된 것을 볼 수 있다.

1. 백테스팅
   ```python InSample_Result = pd.DataFrame(np.dot(returns, np.array(portfolios)), columns=[‘MVP’, ‘HRP’], index=returns.index)

OutOfSample_Result = pd.DataFrame(np.dot(returns_test, np.array(portfolios)), columns=[‘MVP’, ‘HRP’], index=returns_test.index)

InSample_Result.cumsum().plot(figsize=(10, 5), title=”In-Sample Results”)

OutOfSample_Result.cumsum().plot(figsize=(10, 5), title=”Out of Sample Results”, style=[’–’, ‘-.’])

![image1.png](/assets/images/Finance_HW3/image23.png)  
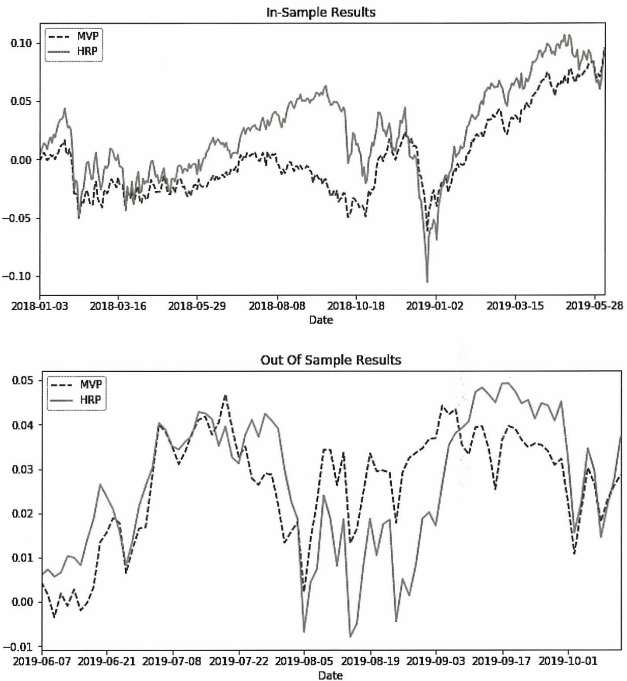
위 차트를 보면 MVP는 샘플 테스트에서 상당한 기간 동안 실적이 저조한 것을 볼 수 있다.  
샘플 외(OOS) 테스트에서는 그나마 짧은 시간동안 HRP보다 더 좋은 성과를 거두긴 했지만 최종 수익률은 저조했다.  

```python
# 샘플 내 결과
stddev = Insample_Result.std() * np.sqrt(252)
sharp_ratio = (Insample_Result.mean() * np.sqrt(252)) / (Insample_Result.std())
Results = pd.DataFrame(dict(stddev=stddev, sharp_ratio=sharp_ratio))
Results

# 샘플 외 결과
stddev_oos = OutOfSample_Result.std() * np.sqrt(252)
sharp_ratio_oos = (OutOfSample_Result.mean() * np.sqrt(252)) / (OutOfSample_Result.std())
Results_oos = pd.DataFrame(dict(stddev_oos=stddev_oos, sharp_ratio_oos=sharp_ratio_oos))
Results_oos

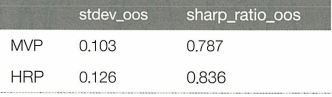
MVP의 샘플 내 결과는 유망해 보이나 샘플 외 결과는 HRP가 더 높은 성과를 보였다. 이는 공분산 추정 오류의 문제를 가지는 MVO이론의 단점을 보여준다.

이러한 결과를 통해 계층적 군집화를 기반으로 한 포트폴리오 배분이 자산을 유사한 특징을 가진 군집으로 더 잘 분리할 수 있음을 확인했다.

※ 나의 생각
테스트셋에서의 HRP모델이 더 높은 샤프비율을 가지긴 했지만 정작 표준편차는 MVP보다 더 높게 나왔다. 위의 파이 차트에서 HRP가 훨씬 더 많이 다각화되었기에 변동성 또한 더 작을 것이라 생각했지만 비체계적 위험이 줄은 대신 체계적 위험이 증가한 것 같다. 또한 분산을 최소화하는것이 목표인 MVP와는 달리 HRP는 자산 군집에 동일한 위험을 분배하는 것을 목표로 하는 Risk Parity에 기반한 전략이기에 분산 자체는 오히려 증가한 것이라 판단된다.
또한 샤프비율의 차이가 너무 근소하기 때문에 다른 기간으로 설정하면 결과가 바뀔수도 있지 않을까라는 생각이 들었다.