Post

금융전략을 위한 머신러닝 chapter 5. 지도 학습: 회귀(시계열 모델)

Posted
By AhnHyoungMin
32 min read
금융전략을 위한 머신러닝 chapter 5. 지도 학습: 회귀(시계열 모델)

Chapter 5. 지도 학습: 회귀(시계열 모델)

  • 금융 기관에 종사하는 애널리스트, 투자 매니저 등 금융권에서 가장 많이 사용하는 머신러닝

  • 금융 산업에서는 상당히 많은 자산 모델링과 예측 문제가 시간 구성요소와 연속 출력의 추정과 관계되기 때문에 시계열 모델을 다루는 것은 필수적이다.

5.1 시계열 모델

5.1.1 시계열 명세

시계열 구성요소

  • 추세 요소
    추세는 시계열에서 일관된 방향으로의 이동을 나타낸다.

결정론적(deterministic): 추세에 대해 근본적인 근거를 제시함.

확률적(stochastic): 시계열의 임의의 특성을 나타낸다.

  • 계절 요소
    많은 시계열에는 계절적 변동이 따른다.

$y_t = S_t + T_t + R_t$
S는 계절요소, T는 추세요소이다. R은 두 요소로 표현하지 못하는 시계열의 나머지 요소를 표현한다.

5.1.2 자기 상관과 고정성

  1. 자기 상관
    시계열에서 연속적 점들이 변화하면 그에 따라 서로 영향을 받는다. 자기 상관은 관측치 간의 유사성을 의미하는 것으로 관측치 간의 시간 지연의 함수로 나타낸다.

자기 회귀: 변수 자신에 대한 회귀가 있음
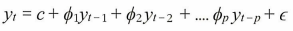
image1.png
→ AR(p) 모델이라고 불리는 p-차 자기 회귀 모델. 여기서 epsilon은 화이트 노이즈이다.
(화이트 노이즈: 상관관계가 없는 임의 변수를 갖는 임의 프로세스로 평균이 0이고 유한 분산을 가진다.)

  • 자기 회귀 모델은 여러 시계열 패턴을 처리하는데 굉장히 유연하다.
  1. 고정성
    시계열의 통계적 특성이 시간에 걸쳐 변하지 않는다면, 그 시계열은 ‘고정적’이라고 한다.
    → 추세나 계절성을 갖는 시계열은 고정적이지 않은 반면 화이트 노이즈 시계열은 고정적이다.

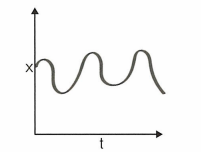
image1.png
위 그래프의 경우 평균, 분산, 공분산이 모두 시간에 따라 일정하기 때문에 고정 시계열이라 할 수 있다.

  • 시계열 예측 모델을 사용하기 위해 비고정 계열을 고정 계열로 변환해주어야 한다.
  1. 디퍼런싱
    디퍼런싱은 시계열을 고정적으로 만드는 방법 중 하나이다.

이 방법은 시계열의 연속항 간의 차를 계산하여 차분 시계열을 생성한다.
→ 이를 통해 추세나 패턴을 제거하고, 변동성의 분포가 일정하게 만들 수 있다.

$y’t = y_t - y{t-1}$
→ 1차 차분

5.1.3 기존 시계열 모델

위에서 설명한 자기 회귀(AR)모델은 시계열의 자기 상관을 설명한다.
이보다 더 널리 사용되는 시계열 예측 모델은 ARIMA이다.

※ ARIMA
고정성을 자기 회귀와 이동평균 모델을 합친 것.

  • AR(p)
    현재의 계열값이 일정한 시간 지연으로 이전 계열값에 따라 달라진다고 가정하고 시계열을 자신의 계열에 회귀하는 자기 회귀

  • I(d)
    통합 차수를 나타낸다. 시계열이 고정성을 갖기 위해 필요한 차의 수라고 할 수 있다.

  • MA(q)
    이동평균을 나타낸다. 현재의 오류가 일정한 시간 지연으로 이전 오류에 따라 달라진다고 가정하고 시계열의 오류를 모델링한다.

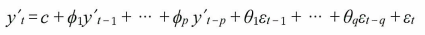
image1.png
이를 ARIMA(p,d,q)라고 한다. 이때 p는 자기 회귀 부분의 차수, d는 1차원 디퍼런싱, q는 이동평균 차수이다.

※ ARIMA 모델 계열 변형

  1. ARIMAX
    외생 변수가 있는 ARIMA모델이다.

  2. SARIMA
    S는 계절성을 나타내며 이 모델은 다른 구성요소를 포함해 시계열에 내재된 계절성 요소를 모델링하는 것을 목표로 한다.

  3. VARIMA
    모델을 다변수로 확장하는 것으로 여러 변수를 동시에 예측할 때 필요하다.

5.1.4 시계열 모델링에 대한 딥러닝 접근방식

ARIMA 등의 기존 시계열 모델은 선형 함수이거나 선형 함수의 단순 변형이기 때문에 왜곡된 데이터나 완전하지 않은 데이터에서는 성능이 좋지 않다.

최근 순환 신경망(RNN)이 시계열 예측을 위한 딥러닝 분야의 발전에 주목을 받고 있음.
→ 구조와 비선형성 같은 패턴을 찾고 다중 입력 변수로 문제를 모델링하기 때문에 상대적으로 불완전한 데이터에 안정적

RNN은 한 단계의 연산에서 얻은 출력을 다음 단계의 연산을 위한 입력으로 사용해 반복적으로 전환되는 상태를 유지한다.

※ 장단기 메모리
장단기 메모리(LSTM)은 RNN의 한 종류로 장기 의존 문제를 해결하기 위해 설계되었다.
이 모델은 셀의 집합으로 되어 있는데, 각 셀은 데이터의 순서를 기억하는 특성이 있으며 데이터의 흐름을 감지하고 저장한다.

각 층은 값이 0에서 1의 값을 가지는 수를 만들어 내고, 이로써 각 셀을 통과하는 데이터의 양을 설명할 수 있다.

각각의 LSTM은 셀의 상태를 통제할 목적으로 세 유형의 게이트를 가진다.

  • 망각 게이트
    0과 1 사이의 수를 출력하는데 1인 경우 완전히 기억하고 0인 경우 완전히 잊어버린다는 의미.

  • 입력 게이트
    셀에 저장할 새로운 데이터를 선택한다.

  • 출력 게이트
    각 셀에서 무엇을 생성할지 결정한다. 생성되는 값은 셀 상태와, 여과되고 새로 추가된 데이터를 기반으로 한다.

5.1.5 지도 학습 모델을 위한 시계열 데이터 수정

image1.png

5.2 실전 문제 1: 주가 예측

  1. 문제 정의
    마이크로소프트 주식의 주 단위 수익을 예측되는 변수로 사용, 무엇이 마이크로소프트 주가에 영향을 주는지 이해한다.

마이크로소프트의 과거 데이터 외에 독립 변수로 사용되는 상관 자산:

  • 주식(IBM과 GOOGL)
  • 환율(미국 달러/엔화 및 파운드/미국 달러)
  • 인덱스(S&P500, 다우존스, 변동성 지수)

2010년부터 10년간의 일별 종가 사용

  1. 데이터와 파이썬 패키지 불러오기
    ```python

    모델 모듈

    from sklearn.linear_model import LinearRegression from sklearn.linear_model import Lasso from sklearn.linear_model import ElasticNet from sklearn.tree import DecisionTreeRegressor from sklearn.neighbors import KNeighborsRegressor from sklearn.svm import SVR from sklearn.ensemble import RandomForestRegressor from sklearn.ensemble import GradientBoostingRegressor from sklearn.ensemble import ExtraTreesRegressor from sklearn.ensemble import AdaBoostRegressor from sklearn.neural_network import MLPRegressor

데이터 분석 및 모델 평가를 위한 함수와 모듈

from sklearn.model_selection import train_test_split from sklearn.model_selection import KFold from sklearn.model_selection import cross_val_score from sklearn.model_selection import GridSearchCV from sklearn.metrics import mean_squared_error from sklearn.feature_selection import SelectKBest from sklearn.feature_selection import chi2, f_regression

딥러닝 모델을 위한 함수와 모듈

from keras.models import Sequential from keras.layers import Dense from keras.optimizers import SGD from keras.layers import LSTM from keras.wrappers.scikit_learn import KerasRegressor

시계열 모델을 위한 함수와 모듈

from statsmodels.tsa.arima_model import ARIMA import statsmodels.api as sm

데이터의 준비와 시각화를 위한 함수와 모듈

판다스, 판다스 데이터리더, 넘파이, 맷플롯립

import numpy as np import pandas as pd import pandas_datareader.data as web from matplotlib import pyplot from pandas.plotting import scatter_matrix import seaborn as sns from sklearn.preprocessing import StandardScaler from pandas.plotting import scatter_matrix from statsmodels.graphics.tsaplots import plot_acf

1
2
3
4
5
6
7
8
9

이후 yfinance와 FRED에서 데이터 불러오기   
```python
stk_tickers = ['MSFT', 'IBM', 'GOOGL']
ccy_tickers = ['DEXJPUS', 'DEXUSUK']
idx_tickers = ['SP500', 'DJIA', 'VIXCLS']
stk_data = web.DataReader(stk_tickers, 'yahoo')
ccy_data = web.DataReader(ccy_tickers, 'fred')
idx_data = web.DataReader(idx_tickers, 'fred')

다음으로는 독립변수와 종속변수를 정의한다. 종속변수는 MSFT의 주간 수익이며 한 주의 거래일을 5일로 가정하고 수익을 계산한다.

독립변수로는 IBM과 GOOGL의 5일 지연 수익, 환율, 인덱스 사용. MSFT의 5일, 15일, 30일, 60일 지연 수익을 함께 사용한다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

return_period = 5

Y = np.log(stk_data.loc[:, ('Adj Close', 'MSFT')]).diff(return_period).\
    shift(-return_period)
Y.name = Y.name[1] + '_pred'

X1 = np.log(stk_data.loc[:, ('Adj Close', ('GOOGL', 'IBM'))]).diff(return_period)
X1.columns = X1.columns.droplevel()

X2 = np.log(ccy_data).diff(return_period)

X3 = np.log(idx_data).diff(return_period)

X4 = pd.concat([np.log(stk_data.loc[:, ('Adj Close', 'MSFT')]).diff(i)
                for i in [return_period, return_period*3, return_period*6, return_period*12]], axis=1).dropna()
X4.columns = ['MSFT_DT', 'MSFT_3DT', 'MSFT_6DT', 'MSFT_12DT']

X = pd.concat([X1, X2, X3, X4], axis=1)

dataset = pd.concat([Y, X], axis=1).dropna().iloc[::return_period, :]
Y = dataset.loc[:, Y.name]
X = dataset.loc[:, X.columns]
  1. 탐색적 데이터 분석
1

dataset.head()

image1.png

데이터간의 관계를 이해하기 위해 산점도와 상관행렬 확인.

1
2
3
4

correlation = dataset.corr()
pyplot.figure(figsize=(15, 15))
pyplot.title('Correlation Matrix')
sns.heatmap(correlation, vmax=1, square=True, annot=True, cmap='cubehelix')

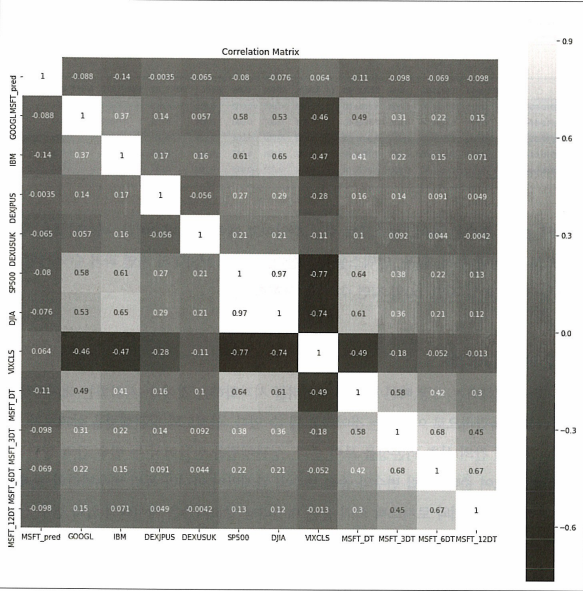
image1.png
→ 변동성 지수 대비 자산 수익 간에 강한 음의 상관관계가 있음을 직관적으로 알 수 있다.

1
2
3

pyplot.figure(figsize=(15, 15))
scatter_matrix(dataset, figsize=(12, 12))
pyplot.show()

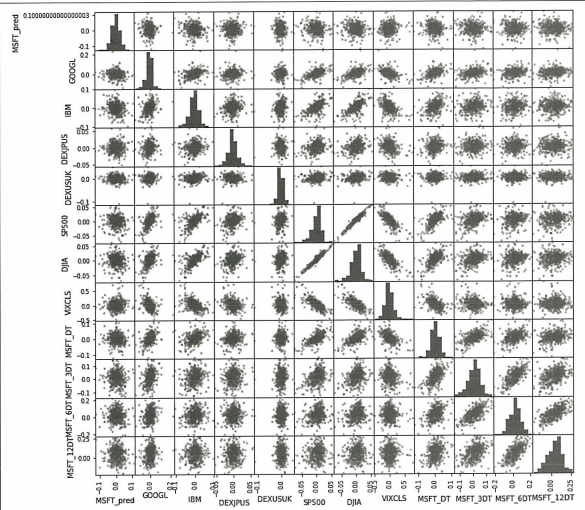
image1.png
독립변수와 종속변수간 관계는 특별한 관계가 있는 것처럼 보이진 않음.

1
2
3
4
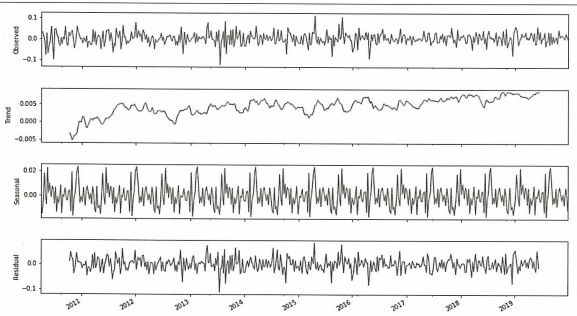
5

res = sm.tsa.seasonal_decompose(Y, freq=52)
fig = res.plot()
fig.set_figheight(8)
fig.set_figwidth(15)
pyplot.show()

image1.png
→ 전반적으로 상향 추세를 보이고 있음.

  1. 데이터 준비
    해당 단계에서는 데이터의 처리와 정리가 이루어지지만 이 데이터의 경우 비교적 깨끗하기 때문에 더이상의 처리는 필요하지 않다.

  2. 모델 평가
    ```python validation_size = 0.2 train_size = int(len(X) * (1 - validation_size))

X_train, X_test = X[0:train_size], X[train_size:len(X)] Y_train, Y_test = Y[0:train_size], Y[train_size:len(X)]

1
2
3
4
5

20%만큼 테스트 셋으로 활용  

```python
num_folds = 10
scoring = 'neg_mean_squared_error'

모델에 있는 다양한 하이퍼파라미터를 최적화하기 위해 10-겹 교차 검증을 사용
평균 제곱 오차 메트릭을 사용하여 알고리즘을 평가한다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

# 예제: 회귀와 트리 회귀 알고리즘
models = []
models.append(('LR', LinearRegression()))
models.append(('LASSO', Lasso()))
models.append(('EN', ElasticNet()))
models.append(('KNN', KNeighborsRegressor()))
models.append(('CART', DecisionTreeRegressor()))
models.append(('SVR', SVR()))

# 예제: 신경망 알고리즘
models.append(('MLP', MLPRegressor()))

# 예제: 앙상블 모델
# 부스팅 방법
models.append(('ABR', AdaBoostRegressor()))
models.append(('GBR', GradientBoostingRegressor()))

# 배깅 방법
models.append(('RFR', RandomForestRegressor()))
models.append(('ETR', ExtraTreesRegressor()))

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

names = []
kfold_results = []
test_results = []
train_results = []

for name, model in models:
    names.append(name)  # k-겹 분석
    kfold = KFold(n_splits=num_folds, random_state=seed)
    
    # 평균 제곱 오차를 양수로 변환함. 낮을수록 좋음.
    cv_results = -1 * cross_val_score(model, X_train, Y_train, cv=kfold, scoring=scoring)
    kfold_results.append(cv_results)
    
    # 총 훈련 기간
    res = model.fit(X_train, Y_train)
    train_result = mean_squared_error(res.predict(X_train), Y_train)
    train_results.append(train_result)

# 테스트 결과
test_result = mean_squared_error(res.predict(X_test), Y_test)
test_results.append(test_result)

각각의 알고리즘에 대해 평가 메트릭의 평균과 표준편차를 계산하고, 차후 모델 평가를 위해 결괏값을 모은다.

1
2
3
4
5
6
7

fig = pyplot.figure()
fig.suptitle('Algorithm Comparison: Kfold results')
ax = fig.add_subplot(111)
pyplot.boxplot(kfold_results)
ax.set_xticklabels(names)
fig.set_size_inches(15, 8)
pyplot.show()

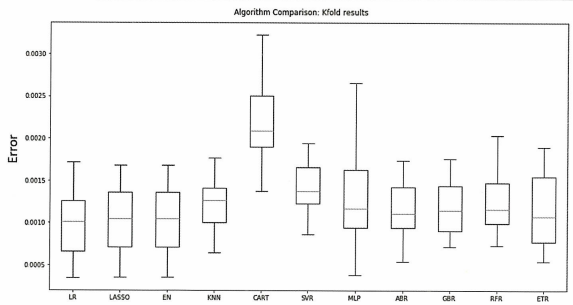
image1.png
박스플롯 결과 라쏘와 엘라스틱 넷을 포함한 선형 회귀와 정규화 회귀 모델이 가장 좋은 성능을 보이고 있음.
→ 종속변수와 독립변수 간에 강한 상관관계가 있음을 알 수 있다.

1
2
3
4
5
6
7
8
9
10
11
12
13

# 알고리즘 비교
fig = pyplot.figure()
ind = np.arange(len(names))  # 그룹의 x 위치
width = 0.35  # 막대 폭
fig.suptitle('Algorithm Comparison')
ax = fig.add_subplot(111)
pyplot.bar(ind - width/2, train_results, width=width, label='Train Error')
pyplot.bar(ind + width/2, test_results, width=width, label='Test Error')
fig.set_size_inches(15, 8)
pyplot.legend()
ax.set_xticks(ind)
ax.set_xticklabels(names)
pyplot.show()

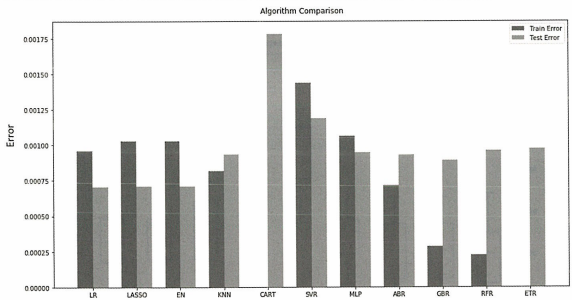
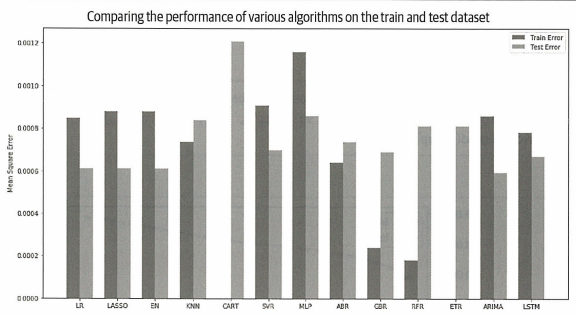
image1.png
CART알고리즘은 훈련 데이터에 과적합된 것을 볼 수 있음.
박스플롯 결과와 비슷하게 선형 모델이 전반적으로 좋은 성능을 보이고 있다.

5.3.2 시계열 기반 모델: ARIMA 및 LSTM

시계열 기반 모델에서는 독립변수로 MSFT의 지연 변수를 포함할 필요가 없기 때문에 첫번째 단계에서 MSFT의 이전 수익을 모델에서 제거하고 다른 모델 변수를 외생 변수로 사용

1
2
3
4
5
6
7
8

X_train_ARIMA = X_train.loc[:, ['GOOGL', 'IBM', 'DEXJPUS', 'SP500', 'DJIA', 'VIXCLS']]
X_test_ARIMA = X_test.loc[:, ['GOOGL', 'IBM', 'DEXJPUS', 'SP500', 'DJIA', 'VIXCLS']]

tr_len = len(X_train_ARIMA)
te_len = len(X_test_ARIMA)
to_len = len(X)
modelARIMA = ARIMA(endog=Y_train, exog=X_train_ARIMA, order=[1, 0, 0])
model_fit = modelARIMA.fit()

(1,0,0)차수로 ARIMA 모델 설정

＊*외생변수를 사용하는 ARIMA모델의 버전은 ARIMAX로 알려졌는데, 여기서 ‘X’는 외생 변수를 나타낸다.**

1
2
3
4

error_Training_ARIMA = mean_squared_error(Y_train, model_fit.fittedvalues)
predicted = model_fit.predict(start=tr_len - 1, end=to_len - 1, exog=X_test_ARIMA)[1:]
error_Test_ARIMA = mean_squared_error(Y_test, predicted)
error_Test_ARIMA

→ 약 0.00059로 ARIMA모델의 오차는 적정 수준이다.

1
2
3
4
5
6
7
8

seq_len = 2  # LSTM에 대한 시퀀스 길이
Y_train_LSTM, Y_test_LSTM = np.array(Y_train)[seq_len-1:], np.array(Y_test)
X_train_LSTM = np.zeros((X_train.shape[0] + 1 - seq_len, seq_len, X_train.shape[1]))
X_test_LSTM = np.zeros((X_test.shape[0], seq_len, X.shape[1]))

for i in range(seq_len):
    X_train_LSTM[:, i, :] = np.array(X_train)[i:X_train.shape[0]+i+1-seq_len, :]
    X_test_LSTM[:, i, :] = np.array(X)[X_train.shape[0]+i+1-seq_len, :]

→ LSTM을 위한 데이터셋 준비. X는 주어진 시간(t)에서의 독립변수 집합이고 Y는 다음 시간(t+1)에서의 목표 변수이다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

# LSTM 망
def create_LSTMmodel(learn_rate=0.01, momentum=0):
    # 모델 생성
    model = Sequential()
    model.add(LSTM(50, input_shape=(X_train_LSTM.shape[1], X_train_LSTM.shape[2])))
    # 필요시 더 많은 셀 추가
    model.add(Dense(1))
    optimizer = SGD(lr=learn_rate, momentum=momentum)
    model.compile(loss='mse', optimizer='adam')
    return model

LSTMModel = create_LSTMmodel(learn_rate=0.01, momentum=0)

# 2부 지도 학습
LSTMModel_fit = LSTMModel.fit(X_train_LSTM, Y_train_LSTM,
                              validation_data=(X_test_LSTM, Y_test_LSTM),
                              epochs=330, batch_size=72, verbose=0, shuffle=False)

→ LSTM 구조 생성. LSTM 층에 있는 50개의 은닉 유닛을 통과해 주식 수익값으로 반환된다.

1
2
3
4

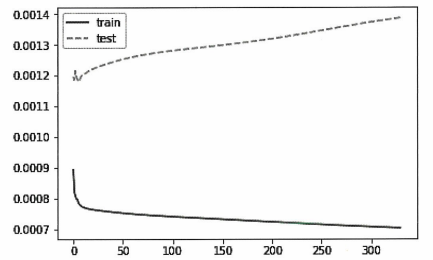
pyplot.plot(LSTMModel_fit.history['loss'], label='train')
pyplot.plot(LSTMModel_fit.history['val_loss'], '--', label='test')
pyplot.legend()
pyplot.show()

image1.png

1
2
3
4
5
6
7
8
9
10
11

error_Training_LSTM = mean_squared_error(Y_train_LSTM, LSTMModel.predict(X_train_LSTM))
predicted = LSTMModel.predict(X_test_LSTM)
error_Test_LSTM = mean_squared_error(Y_test, predicted)

test_results.append(error_Test_ARIMA)
test_results.append(error_Test_LSTM)
train_results.append(error_Training_ARIMA)
train_results.append(error_Training_LSTM)

names.append("ARIMA")
names.append("LSTM")

image1.png
시계열 기반 ARIMA모델이 선형 회귀(LR), 라쏘 회귀(LASSO), 엘라스틱 넷(EN)과 비슷한 성능을 보이고 있다.

LSTM모델 성능도 괜찮지만 ARIMA모델이 LSTM모델보다 테스트셋 오차가 더 적다.
→ 모델 튜닝을 위해 ARIMA모델 선택

  1. 모델 튜닝 및 격자 탐색
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

def evaluate_arima_model(arima_order):
    # predicted = list()
    modelARIMA = ARIMA(endog=Y_train, exog=X_train_ARIMA, order=arima_order)
    model_fit = modelARIMA.fit()
    error = mean_squared_error(Y_train, model_fit.fittedvalues)
    return error

# ARIMA 모델에 대한 p, d, q 값 조합 평가
def evaluate_models(p_values, d_values, q_values):
    best_score, best_cfg = float("inf"), None
    for p in p_values:
        for d in d_values:
            for q in q_values:
                order = (p, d, q)
                try:
                    mse = evaluate_arima_model(order)
                    if mse < best_score:
                        best_score, best_cfg = mse, order
                    print('ARIMA%s MSE=%.7f' % (order, mse))
                except:
                    continue
    print('Best ARIMA%s MSE=%.7f' % (best_cfg, best_score))

# 매개변수 평가
p_values = [0, 1, 2]
d_values = range(0, 2)
q_values = range(0, 2)
warnings.filterwarnings("ignore")
evaluate_models(p_values, d_values, q_values)

image1.png
위 결과를 통해 (2,0,1) 차수를 갖는 ARIMA 모델이 격자 탐색에서 가장 좋은 성능을 보임을 알 수 있다.

  1. 모델 확정
1
2
3
4
5
6
7
8
9

# 모델 준비
modelARIMA_tuned = ARIMA(endog=Y_train, exog=X_train_ARIMA, order=[2, 0, 1])
model_fit_tuned = modelARIMA_tuned.fit()

# 검증셋에 대한 정확도 추정
# estimate accuracy on validation set
predicted_tuned = model_fit_tuned.predict(start=tr_len - 1, end=to_len - 1, exog=X_test_ARIMA)[1:]
print(mean_squared_error(Y_test, predicted_tuned))
# output: 0.0005970582461404503

→ 테스트셋에 대한 모델의 평균 제곱 오차가 좋게 나온다.

1
2
3
4
5
6
7
8
9

# 실제 데이터와 예측 데이터 그래프
predicted_tuned.index = Y_test.index
pyplot.plot(np.exp(Y_test).cumprod(), 'r', label='actual')

# t와 a 분리하여 그리기
pyplot.plot(np.exp(predicted_tuned).cumprod(), 'b--', label='predicted')
pyplot.legend()
pyplot.rcParams["figure.figsize"] = (8, 5)
pyplot.show()

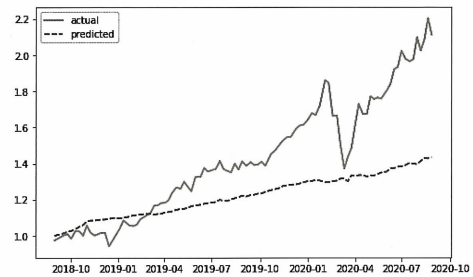
image1.png
차트를 보면 모델이 추세를 잘 따라가고 있음을 알 수 있다.
하지만 이 모델은 현시점까지 관측된 데이터가 주어졌을 때 다음 날의 수익을 계산하기 때문에 테스트셋의 처음에서 멀어질수록 실제 데이터에서 벗어날 것으로 예상된다.

chapter 6. 지도 학습: 분류

6.3 실전 문제 3: 비트코인 거래 전략

비트코인은 익명의 사토시 나카모토가 2009년에 오픈 소스로 처음 출시한 이래 가장 오랫동안 실행되고 가장 잘 알려진 암호화폐이다.

암호화폐 거래의 주요 단점은 시장의 변동성이다. 암호화폐 시장은 연중 무휴로 운영되기 때문에 빠르게 변화하는 시장 역학에 대응해 암호화폐의 위치를 추적하는 것은 굉장히 어렵다.

머신러닝 알고리즘은 다음 날의 움직임을 시장 상승(Long), 시장 하락(Short), 시장 횡보(No Reaction)으로 분류하여 최적의 진입점과 출구점을 결정할 수 있다.

이번 실전 문제에서는 다양한 분류 기반 모델을 활용하여 현재 위치의 신호가 매수 또는 매도인지 예측한다. 시장 가격에서 추세 및 모멘텀 지표를 생성해 예측의 추가 특성으로 활용한다.

  1. 문제 정의
  • 예측되는 변수의 값이 매수는 1, 매도는 0이 된다.
  • 사용할 데이터는 평균 일일 거래량이 가장 많은 비트스탬프 거래소에서 가져온다. 데이터에는 2012년 1월부터 2017년 5월까지의 가격이 들어 있다.
  1. 데이터 및 패키지 불러오기
1

dataset = pd.read_csv('BitstampData.csv')
  1. 탐색적 데이터 분석
1
2

dataset.shape
# output: (2841377,8)

1
2
3

# 데이터 확인
set_option('display.width', 100)
dataset.tail(2)

image1.png

  1. 데이터 준비
    ```python dataset[dataset.columns.values] = dataset[dataset.columns.values].ffill()

dataset = dataset.drop(columns=[‘Timestamp’])

1
2
3
4
5
6
7
8
9
10
11

Nan값은 마지막 값으로 바꿔서 데이터를 정리하고 Timestamp 열은 모델링에 유용하지 않으므로 데이터셋에서 삭제  

```python
# 좁은 윈도우에 짧은 단순 이동평균 생성
dataset['short_mavg'] = dataset['Close'].rolling(window=10, min_periods=1, center=False).mean()

# 긴 윈도우에 긴 단순 이동평균 생성
dataset['long_mavg'] = dataset['Close'].rolling(window=60, min_periods=1, center=False).mean()

# 신호 생성
dataset['signal'] = np.where(dataset['short_mavg'] > dataset['long_mavg'], 1.0, 0.0)

단기 가격을 10일 이동평균으로, 장기 가격을 60일 이동평균으로 정의하고 단기가격이 장기가격보다 더 높으면 라벨 1로 표시하기로, 그렇지 않으면 0으로 표시하기로 설정

※ 주요 모멘텀 지표

  • 이동평균
    시계열의 잡음을 줄여 가격 추세를 보여준다.

  • 스토캐스틱 오실레이터(%K)
    특정 기간 동안 주식의 종가를 이전 가격 범위와 비교하는 모멘텀 지표이다.
    %K와 %D는 각각 느린 지표, 빠른 지표를 나타낸다. 빠른 지표는 느린 지표보다 기본 주가의 변동에 더 민감하기 때문에 많은 거래 신호를 생성할 확률이 있다.

  • 상대 강도 지수(RSI)
    주식 또는 기타 자산 가격의 과매수 또는 과매도 상태를 평가하기 위해 최근 가격 변동의 규모를 측정하는 모멘텀 지표이다. RSI의 범위는 0~100까지이며 70에 가까워지면 과매수, 30에 가까워지면 과매도임을 나타낸다.

  • 변화율(ROC)
    현재 가격과 n기간 과거 가격 사이의 백분율 변화를 측정하는 모멘텀 오실레이터이다. ROC값이 높은 자산은 과매수 확률이 높은 것으로 본다. ROC가 낮을수록 과매도 확률이 높다.

  • 모멘텀
    주가 또는 거래량의 가속 속도, 즉 가격이 변하는 속도이다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72

# 지수 이동평균 계산
def EMA(df, n):
    EMA = pd.Series(df['Close'].ewm(span=n, min_periods=n).mean(), name='EMA_' + str(n))
    return EMA

dataset['EMA10'] = EMA(dataset, 10)
dataset['EMA30'] = EMA(dataset, 30)
dataset['EMA200'] = EMA(dataset, 200)
dataset.head()

# 변화율 계산
def ROC(df, n):
    M = df.diff(n - 1)
    N = df.shift(n - 1)
    ROC = pd.Series(((M / N) * 100), name='ROC_' + str(n))
    return ROC

dataset['ROC10'] = ROC(dataset['Close'], 10)
dataset['ROC30'] = ROC(dataset['Close'], 30)

# 가격 모멘텀 계산
def MOM(df, n):
    MOM = pd.Series(df.diff(n), name='Momentum_' + str(n))
    return MOM

dataset['MOM10'] = MOM(dataset['Close'], 10)
dataset['MOM30'] = MOM(dataset['Close'], 30)

# 상대 강도 지수 계산
def RSI(series, period):
    delta = series.diff().dropna()
    u = delta * 0
    d = u.copy()
    u[delta > 0] = delta[delta > 0]
    d[delta < 0] = -delta[delta < 0]
    u[u.index[period-1]] = np.mean(u[:period]) # first value is sum of avg gains
    u = u.drop(u.index[:(period-1)])
    d[d.index[period-1]] = np.mean(d[:period]) # first value is sum of avg losses
    d = d.drop(d.index[:(period-1)])
    rs = u.ewm(com=period-1, adjust=False).mean() / d.ewm(com=period-1, adjust=False).mean()
    return 100 - 100 / (1 + rs)

dataset['RSI10'] = RSI(dataset['Close'], 10)
dataset['RSI30'] = RSI(dataset['Close'], 30)
dataset['RSI200'] = RSI(dataset['Close'], 200)

# 확률 변동 계산
def STOK(close, low, high, n):
    STOK = ((close - low.rolling(n).min()) / (high.rolling(n).max() - low.rolling(n).min())) * 100
    return STOK

def STOD(close, low, high, n):
    STOK = ((close - low.rolling(n).min()) / (high.rolling(n).max() - low.rolling(n).min())) * 100
    STOD = STOK.rolling(3).mean()
    return STOD

dataset['%K10'] = STOK(dataset['Close'], dataset['Low'], dataset['High'], 10)
dataset['%D10'] = STOD(dataset['Close'], dataset['Low'], dataset['High'], 10)

dataset['%K30'] = STOK(dataset['Close'], dataset['Low'], dataset['High'], 30)
dataset['%D30'] = STOD(dataset['Close'], dataset['Low'], dataset['High'], 30)
dataset['%K200'] = STOK(dataset['Close'], dataset['Low'], dataset['High'], 200)
dataset['%D200'] = STOD(dataset['Close'], dataset['Low'], dataset['High'], 200)

# 이동평균 계산
def MA(df, n):
    MA = pd.Series(df['Close'].rolling(n, min_periods=n).mean(), name='MA_' + str(n))
    return MA

dataset['MA21'] = MA(dataset, 10)
dataset['MA63'] = MA(dataset, 30)
dataset['MA252'] = MA(dataset, 200)

→ 해당 코드는 예측에 유용한 몇 가지 특성을 생성하는 방법에 대한 코드이다.

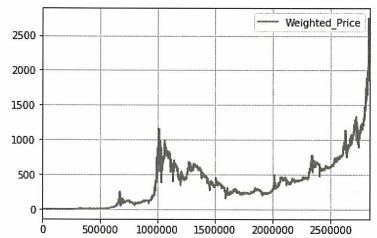
1
2

dataset[['Weighted_Price']].plot(grid=True)
plt.show()

image1.png

1
2
3

fig = plt.figure()
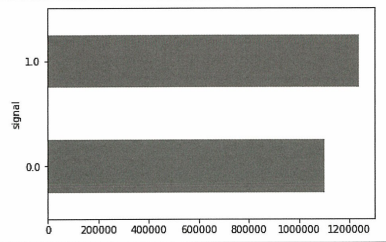
plot = dataset.groupby(['signal']).size().plot(kind='barh', color='red')
plt.show()

image1.png

  1. 알고리즘 및 모델 평가
1
2
3
4
5
6
7
8
9

# 검증 데이터셋 분할
subset_dataset = dataset.iloc[-100000:]
Y = subset_dataset["signal"]
X = subset_dataset.loc[:, dataset.columns != 'signal']
validation_size = 0.2

seed = 1
X_train, X_validation, Y_train, Y_validation = \
    train_test_split(X, Y, test_size=validation_size, random_state=1)

데이터셋을 훈련셋(80%), 테스트셋(20%)로 분할한다.

1
2
3

# 분류 옵션 테스트
num_folds = 10
scoring = 'accuracy'

→ 데이터에 심각한 클래스 불균형이 없기 때문에 정확도를 평가 메트릭으로 사용할 수 있다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

models = []
models.append(('LR', LogisticRegression(n_jobs=-1)))
models.append(('LDA', LinearDiscriminantAnalysis()))
models.append(('KNN', KNeighborsClassifier()))
models.append(('CART', DecisionTreeClassifier()))
models.append(('NB', GaussianNB()))

# 신경망
models.append(('NN', MLPClassifier()))

# 앙상블 모델 - 부스팅 방법
models.append(('AB', AdaBoostClassifier()))
models.append(('GBM', GradientBoostingClassifier()))

# 배깅 방법
models.append(('RF', RandomForestClassifier(n_jobs=-1)))

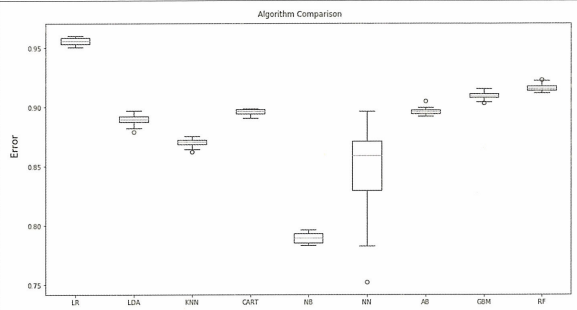
image1.png
데이터셋의 방대한 크기, 많은 특성, 예측되는 변수와 특성 간의 예상되는 비선형 관계를 고려하면 앙상블 모델이 우세하다. 그 중 랜덤 포레스트가 최고의 성능을 보인다.

  1. 모델 튜닝 및 격자 탐색
1
2
3
4
5
6
7
8
9
10
11
12
13

n_estimators = [20, 80]
max_depth = [5, 10]
criterion = ["gini", "entropy"]

param_grid = dict(n_estimators=n_estimators, max_depth=max_depth, criterion=criterion)

model = RandomForestClassifier(n_jobs=-1)
kfold = KFold(n_splits=num_folds, random_state=seed)
grid = GridSearchCV(estimator=model, param_grid=param_grid, scoring=scoring, cv=kfold)

grid_result = grid.fit(X_train, Y_train)
print("Best: %f using %s" % (grid_result.best_score_, grid_result.best_params_))
# output: Best: 0.903438 using {'criterion': 'gini', 'max_depth': 10, 'n_estimators': 80}
  1. 모델 확정
    ```python

    모델 준비

    model = RandomForestClassifier(criterion=’gini’, n_estimators=80, max_depth=10) model.fit(X_train, Y_train)

검증셋에 대한 정확도 추정

predictions = model.predict(X_validation) print(accuracy_score(Y_validation, predictions))

output: 0.9075

1
2
3
4
5
6
7
8

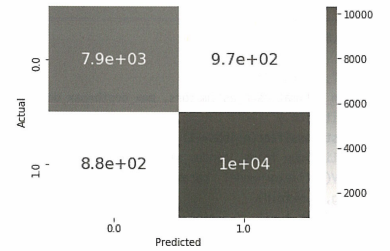
![image1.png](/assets/images/Finance_HW2/image19.png)   
모델의 정확도도 90.75%로 매우 우수한 성능을 보이고 혼동 행렬 또한 전반적으로 모델 성능이 합리적임을 볼 수 있다.  


```python
Importance = pd.DataFrame({'Importance': model.feature_importances_ * 100}, index=X.columns)
Importance.sort_values('Importance', axis=0, ascending=True).plot(kind='barh', color='r')
plt.xlabel('Variable Importance')

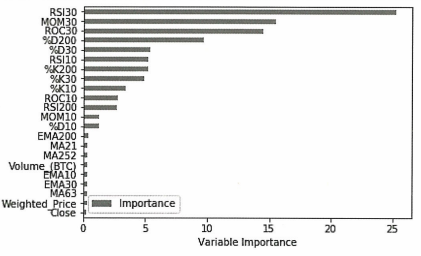
image1.png
지난 30일 동안의 RSI 및 MOM 모멘텀 지표가 가장 중요한 두가지 특성으로 나타났다.

1
2
3
4
5
6
7
8
9
10
11
12

backtestdata = pd.DataFrame(index=X_validation.index)
backtestdata['signal_pred'] = predictions
backtestdata['signal_actual'] = Y_validation
backtestdata['Market Returns'] = X_validation['Close'].pct_change()
backtestdata['Actual Returns'] = backtestdata['Market Returns'] * backtestdata['signal_actual'].shift(1)
backtestdata['Strategy Returns'] = backtestdata['Market Returns'] * backtestdata['signal_pred'].shift(1)

backtestdata = backtestdata.reset_index()
backtestdata.head()

backtestdata[['Strategy Returns', 'Actual Returns']].cumsum().hist()
backtestdata[['Strategy Returns', 'Actual Returns']].cumsum().plot()

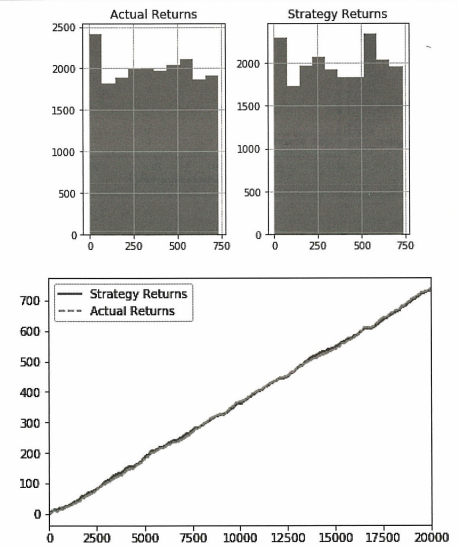
image1.png
백테스팅 결과 실제 시장수익률에서 크게 벗어나지 않으며 모멘텀 거래 전략은 매수 또는 매도를 진행할 가격 방향을 더 잘 예측했다.

KHUDA, Finance
KHUDA Quant ML
This post is licensed under CC BY 4.0 by the author.

Trending Tags

ML KHUDA Quant FBA_Quant