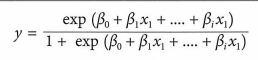Post

금융전략을 위한 머신러닝 chapter 3. 인공 신경망 & chapter 4. 지도 학습: 모델 및 개념

Posted
By AhnHyoungMin
37 min read
금융전략을 위한 머신러닝 chapter 3. 인공 신경망 & chapter 4. 지도 학습: 모델 및 개념

chapter 3. 인공 신경망

머신러닝 기법 중 인공신경망은 인공 뉴런이라고 불리는 노드가 연결된 집합체로, 연산을 수행하는 시스템이다.

신호를 받은 인공 뉴런은 신호를 처리하고 그다음 연결된 뉴런에 전달한다.

3.1 구조, 훈련, 하이퍼파라미터

인공 신경망은 모델을 거쳐 얻은 결과와 예상한 결과를 비교하는 방식으로 훈련 단계를 거친다.

3.1.1 구조

  1. 뉴런
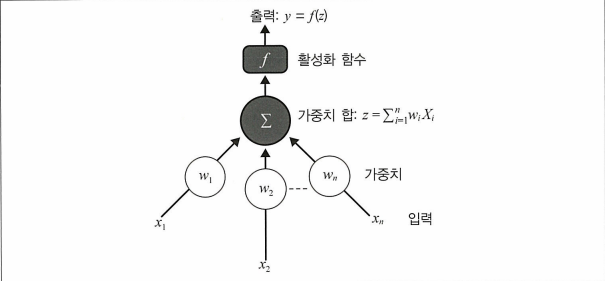
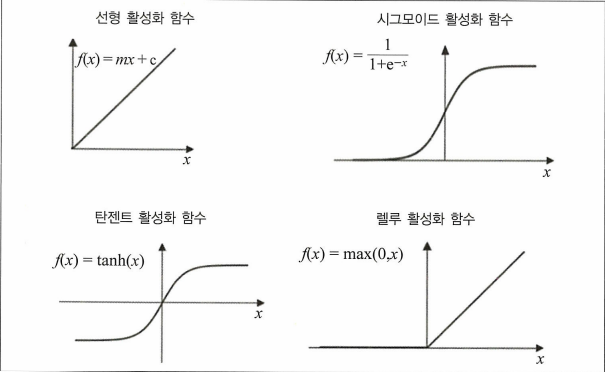
    image1.png
    뉴런은 입력 $(x_1, x_2, … ,x_n)$ 을 받아서 훈련 매개변수를 적용해 가중치합을 생성한 후 그 합을 출력하도록 하는 활성화 함수 f에 전달한다.

  2. 계층
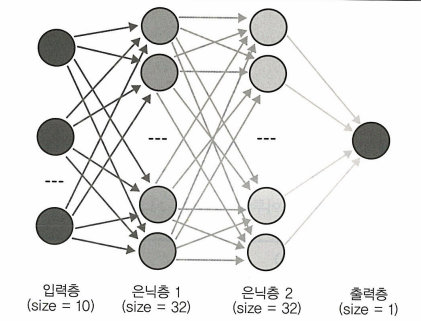
    위의 그림처럼 하나의 뉴런에서 나온 출력값만으로는 복잡한 일을 수행하는 모델을 만들 수 없다.
    → 은닉층(Hidden layer)를 넣어줌으로써 뉴런을 쌓는다.

  3. 가중치
    뉴런 가중치는 단위 간의 연결 강도를 나타내고 입력이 출력에 영향을 미치는 정도를 수치화한다.

3.1.2 훈련

하나의 신경망을 훈련한다. → 인공 신경망에서 정의한 모든 가중치를 적합하게 조정한다.

  1. 순전파
    하위 층부터 상위층으로 활성화 연산을 적용하고 반복적으로 수행하는 과정.

  2. 역전파
    예측값과 기댓값의 차이를 손실함수로 변환하여 손실함수를 최소화하는 방식.
    → 이때 사용되는 최적화 방법이 경사 하강법 이다.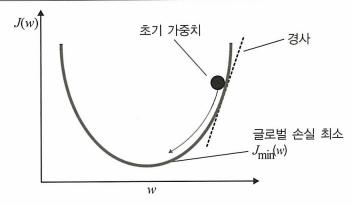 image1.png
    주어진 점에서 가중치 w에 대한 손실함수의 경사가 낮아지는 방향으로 이동하여 가장 낮은 값에 도달할 때까지 진행.

마지막 층에서부터 역방향으로 미분을 적용해 나가는 과정에서 역전파 활용

3.1.3 하이퍼파라미터

  1. 은닉층 및 노드 수
    잘 일반화할 수 있는 훈련된 망을 갖기 위해선 은닉층과 각 은닉층 노드의 개수를 최적화해야 한다.(과대적합 or 과소적합 방지)

※ 노드의 경우 이 책에서는 경험적으로 봤을 때 입력층의 크기와 출력층의 크기의 중간값으로 은닉층 노드 수를 설정하면 된다고 함.

  1. 학습률
    얼마나 빨리 또는 느리게 가중치값이 변할지 결정하는 학습률을 조정해주어야 한다.
    학습률은 적당한 시간 안에 수렴할 만큼 커야 하고 손실 함수의 최솟값을 찾을 만큼 작아야 한다.

  2. 활성화 함수
    각각의 활성화 함수를 적용해보고 더 효율적인 훈련 과정을 보여주는 함수를 선택해야 한다.
    image1.png

  3. 비용 함수
    비용함수(손실함수)를 선택하여 인공신경망 성능의 정도와 얼마나 실험 데이터에 적합한지를 측정해햐한다.
    • 평균 제곱 오차(MSE)
    • 교차 엔트로피(로그 손실)
  4. 최적화 알고리즘
    손실함수를 최소화하는 방향으로 가중치를 갱신하기 위해 최적화 알고리즘 기법을 선택해야한다.
    • 모멘텀: 이전 경사를 현재 단계에서 참조. 가중치의 이전 갱신이 현재 갱신과 같은 방향으로 갈 경우 더 큰 단계 선택, 서로 상반될 경우 더 작은 단계 선택.
    • 에이다그레이드(조정적 경사 알고리즘): 자주 발생하는 특성들과 관련된 매개변수는 작게 갱신, 드물게 발생하는 특성들과 관련된 매개변수는 크게 갱신.
    • 알엠에스프랍(RMSProp): 학습률이 자동으로 변하고 각 매개변수의 학습률이 다르다.
    • 아담(조정적 순간 예측): 에이다그레이드 + 알엠에스프랍. 인기가 가장 많은 경사하강 최적화 알고리즘이다.

  5. 에폭
    전체 훈련 데이터셋에 대해 신경망을 갱신하는 주기.

  6. 배치 크기
    정방향/역방향 전달로 훈련하는 예제의 횟수를 의미. 배치 크기가 클수록 메모리 공간이 많이 필요하다.

3.2 인공 신경망 모델 생성

1
2
3
4
5
6
7
8
9
10
11
12

from keras.models import Sequential
from keras.layers import Dense
import numpy as np

data = np.random.random((1000, 10))
Y = np.random.randint(2, size=(1000, 1))
model = Sequential()

model = Sequential()
model.add(Dense(32, input_dim=10, activation='relu'))
model.add(Dense(32, activation='relu'))
model.add(Dense(1, activation='sigmoid'))

image1.png

1
2
3
4
5
6
7
8
9

# cross-entropy 사용
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])

# 모델 적합화
model.fit(data, Y, nb_epoch=10, batch_size=32)

# 모델 평가
scores = model.evaluate(X_test, Y_test)
print("%s: %.2f%%" % (model.metrics_names[1], scores[1] * 100))

chapter 4. 지도 학습: 모델 및 개념

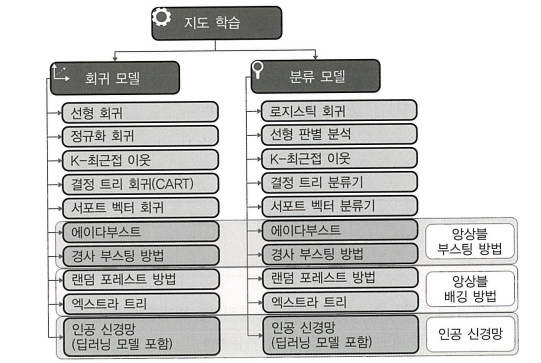
지도 학습은 선택된 알고리즘이 주어진 입력값을 이용해 타겟을 적합화하는 머신러닝 영역이다.

  • 지도 학습은 회귀, 분류 두 개의 알고리즘으로 나눈다.
  • 회귀 알고리즘: 입력값을 바탕으로 출력을 예측
  • 분류 알고리즘: 주어진 데이터셋이 어느 분류에 속하는지 확인

지도 학습 모델은 금융 분야 중 머신러닝 모델 분류에서 가장 많이 사용되는 대표적인 방법이다.
알고리즘 거래에 적용하는 많은 알고리즘이 지도 학습을 기반으로 하는데 이는 효율적으로 훈련할 수 있고, 이상치 금융 데이터에 비교적 안정적이고 금융 이론(CAPM, FF3)과 강한 연관성이 있기 때문이다.

회귀 알고리즘 - 포트폴리오 관리, 파생상품 가격 책정
분류 알고리즘 - 사기 감지, 신용 점수, 매수/매도 추천

4.1 지도 학습 모델: 개념

image1.png

4.1.1 선형 회귀(최소 제곱)

$y = \beta_0 + \beta_1x_1 + … + \beta_ix_i$
$\beta_0$ : intercept(y절편)
$\beta_1,…,\beta_i$ : 회귀계수

1
2
3

from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X, Y)

잔차 제곱합(RSS)으로 비용 함수를 정의하고 해당 함수를 최소화하는 방식으로 모델 훈련이 이루어진다.
$RSS = \sum_{i=1}^{n} \left( y_i - \beta_0 - \sum_{j=1}^{n} \beta_j x_{ij} \right)^2$

이후 격자 탐색을 통해 가능한 하이퍼파라미터 조합을 모두 생성하고 그 조합을 하나씩 이용해 모델을 훈련한다.

1
2

model = LinearRegression()
param_grid = {'fit_intercept': [True, False]}

선형회귀의 하이퍼파라미터는 fit_intercept이고 True/False 통해 이 모델에 인터셉트를 계산할지 말지를 결정한다.

1
2

grid = GridSearchCV(estimator=model, param_grid=param_grid, scoring='r2', cv=kfold)
grid_result = grid.fit(X, Y)

※ 장단점

  • 가장 큰 장점은 해석하기 쉽다는 것.
  • 하지만 예측되는 변수와 예측 변수의 관계가 비선형인 경우에는 올바르게 작동하지 않을 수 있다.
  • 다중공선성이 없다는 가정을 따라야 한다.

4.1.2 정규화 회귀

선형회귀 모델에서 독립변수가 너무 많으면 모델이 훈련 데이터에 과대적합되는 문제가 발생한다.
→ 과적합을 조절하기 위해 정규화 활용

정규화: 손실함수에 패널티 항을 추가해 계수가 큰 값에 이르는 것을 억제하는 방법.

  1. 일부 계수를 0에 근접시킴으로써 복잡한 모델을 더 잘 일반화될 수 있는 모델로 적합화할 수 있다.
  2. 영향이 가장 큰 매개변수만을 취하여 해석을 용이하게 할 수 있다.

  • L1 정규화 혹은 라쏘 회귀
    $\text{CostFunction} = RSS + \lambda \cdot \sum_{j=1}^{p} |\beta_j|$

  • 라쏘 회귀는 회귀 계수가 완전히 0이 될 수 있다.
  • 정규화 매개변수 값이 클수록 더 많은 특성이 0으로 수렴한다.
    → 라쏘 회귀는 과적합 방지 뿐만 아니라 특성 선택에도 유용
1
2
3

from sklearn.linear_model import Lasso
model = Lasso()
model.fit(X,Y)

  • L2 정규화 혹은 릿지 회귀
    $\text{CostFunction} = RSS + \lambda \cdot \sum_{j=1}^{p} \beta_j^2$

  • 릿지 회귀는 회귀 계수가 0에 가까워지긴 하지만 완전히 0이 되지는 않는다.

1
2
3

from sklearn.linear_model import Ridge
model = Ridge()
model.fit(X,Y)

  • 엘라스틱 넷
    $\text{CostFunction} = RSS + \lambda \cdot \left( \frac{(1 - \alpha)}{2} \cdot \sum_{j=1}^{p} \beta_j^2 + \alpha \cdot \sum_{j=1}^{p} |\beta_j| \right)$

  • 릿지와 라쏘를 합한 방식
  • $\lambda$ 뿐만 아니라 알파 매개변수도 조절할 수 있다.($\alpha = 0 : Ridge, \alpha = 1 : Lasso$)
1
2
3

from sklearn.linear_model import ElasticNet
model = ElasticNet()
model.fit(X,Y)

4.1.3 로지스틱 회귀

분류 문제에 가장 널리 사용되는 알고리즘으로 출력 클래스의 확률 분포를 모델링한다.
사옹되는 함수는 x에 대한 선형함수이며 출력값은 0~1사이의 값을 가진다.
→ sigmoid함수를 적용하여 0과 1 사이의 확률을 출력한다.

image1.png

비용 함수는 실제값이 0일 때 얼마나 자주 1로 예측했는지를 측정값으로 나타낸다.

  • 로지스틱 회귀 계수를 훈련하는 데 최대 우도 측정(MLE)과 같은 기술을 사용
    (MLE : 관찰된 데이터가 사실일 확률이 가장 높다는 통계적 모델의 가정하에 확률 분포의 변수를 예측하는 방법)
1
2
3

from sklearn.linear_model import LogisticRegression
model = LogisticRegression()
model.fit(X,Y)
  • 로지스틱 회귀도 정규화 적용 가능

※ 장단점

  • 구현하기 쉽고, 해석성이 좋으며, 선형적으로 분리된 클래스에서 잘 작동한다.
  • 특성의 수가 커지면 모델이 과적합될 수 있다는 단점이 있다.

4.1.4 서포트 벡터 머신

서포트 벡터 머신(SVM)의 목적은 마진을 최대화하는 것.
(마진: 분리 초평면(or 결정선)과 이 초평면에 가장 가까이 있는 훈련 샘플 사이의 거리)
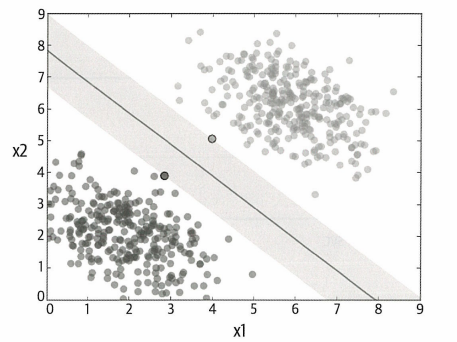
image1.png
마진은 마진 영역의 중앙선에서 가장 가까운 포인트까지의 수직거리로 계산된다. SVM은 모든 데이터 포인트에 대해 균일하게 구분짓는 최대 마진 영역을 계산한다.

실제 데이터는 깔끔하게 분류되기 어렵기 때문에 중앙선의 마진을 최대화하는 조건을 완화해야 한다.
→ 일부 테스트 데이터 포인트가 중앙선 안에 들어오게 된다.

C는 튜닝 매개변수로, 마진 내에서 오차를 얼마나 허용할 것인지를 결정하는 값
→ C값이 클수록 데이터를 더 정확하게 나누려고 한다.

  • 일부 경우에는 초평면 혹은 선형 결정 영역을 찾지 못할 수 있는데 이때는 커널을 사용한다.
    (커널: SVM이 많은 데이터를 쉽게 처리할 수 있도록 입력 데이터를 변환하는 것)
    → 커널을 통해 원래 데이터를 고차원에 투영하여 데이터를 더 잘 분류하게 된다.
1
2
3
4
5
6
7
8
9

# 회귀 
from sklearn.svm import SVR
model = SVR()
model.fit(X, Y)

# 분류
from sklearn.svm import SVC
model = SVC()
model.fit(X, Y)
  • 커널을 선택하여 입력 변수를 투영하는 방식을 결정할 수 있다. 보편적으로 선형 커널 또는 RBF 사용
  • 패널티 매개변수 값이 크면 최적화는 마진이 작은 추평면을 선택한다. 로그 스케일로 10에서 1000사이의 값이 적당하다.

※ 장단점

  • SVM은 과적합에 안정적이어서 특히 고차원 영역일수록 좋다.
  • 비선형 관계를 다루는 커널이 다양하고 데이터의 분포도를 요하지 않는다는 장점이 있다.
  • 학습에 비효율적이고 메모리를 많이 요구하기 때문에 큰 데이터셋에는 성능이 좋지 않다.
  • 데이터 스케일링이 필요하고 많은 하이퍼파라미터의 의미가 직관적이지 않다.

4.1.5 K-최근접 이웃

새로운 데이터를 전체 훈련셋을 통해 그 데이터에 가장 근접한 K개의 이웃을 찾고 그 K개에 대한 출력 변수를 도출하는 방식

훈련 데이터셋에서 새로운 입력에 가장 유사한 K개의 예가 무엇인지 결정하기 위해 거리를 측정한다.
→ 유클리언 디스턴스 or 맨해튼 디스턴스

유클리언 디스턴스: $d(a, b) = \sqrt{\sum_{i=1}^{n} (a_i - b_i)^2}$
맨해튼 디스턴스: $d(a, b) = \sum_{i=1}^{n} |a_i - b_i|$

1
2
3
4
5
6
7
8
9

# 분류
from sklearn.neighbors import KNeighborsClassifier
model = KNeighborsClassifier()
model.fit(X, Y)

# 회귀
from sklearn.neighbors import KNeighborsRegressor
model = KNeighborsRegressor()
model.fit(X, Y)
  • n_neighbors(이웃수)는 1~20 사이가 적당
  • 이웃을 구성하는 데 여러 거리 메트릭 활용 가능. 일반적으로 유클리언, 맨해튼 활용

※ 장단점

  • 학습이 필요 없다.
  • 직관적으로 쉽게 이해할 수 있고 잡음이 있는 데이터에 안정적이어서 이상치를 걸러낼 필요가 없다.
  • 선택할 거리 메트릭이 불명확, 정당화 어려움
  • 매번 계산해야하기 때문에 비용이 높아지고 새로운 예를 예측하는 성능이 느리다.
  • 데이터셋에 잡음이 많아질 경우 결측값을 수동으로 입력하고 이상치를 제거해야 한다.

★ 잡음 관련해서 뭔소린지 모르겠음 ★

4.1.6 선형 판별 분석

선형 판별 분석(LDA)알고리즘은 분류 분별력을 극대화하고 분류 내의 분산을 최소화하는 방식으로 데이터를 저차원 영역에 투영한다.

※ Assumption

  • 데이터는 정규분포를 따른다.
  • 각 속성은 분산이 같고 각 변수의 값은 평균에서 동일한 양으로 변한다.
1
2
3

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
model = LinearDiscriminantAnalysis()
model.fit(X, Y)
  • LDA모델의 핵심 하이퍼파라미터는 차원 축소를 위한 컴포넌트의 수이고, 사이킷런에 있는 n_components로 나타낸다.

※ 장단점
비교적 단순한 모델로 빠르고 쉽게 구현할 수 있다.

  • 특성 스케일링이 필요하고 복잡한 행렬 연산을 요구한다.

4.1.7 분류 트리와 회귀 트리

image1.png
각 노드는 분기점에서의 입력 변수 x이고, 각 트리의 말단에 예측을 위한 출력 변수 y가 있다.

이진 트리를 생성하는 것은 실제로 입력 영역을 나누는 과정이다. 재귀적 이분법이라는 Greedy 알고리즘(매번 최선의 분기를 선택하는 방식)을 이용해 영역을 나눈다.

※ CART 모델 학습
비용함수는 각 구간에 속하는 모든 훈련 샘플에 대해 오차 제곱합으로 나타내어진다.
$\sum^n_{i=1}(y-prediction_i)^2$

분류모델에서는 지니 비용함수 사용.
→ 한 노드에 모여 있는 데이터 포인트들이 얼마나 같은 클래스에 속하는지 표시
$G = \sum^n_{i=1}p_k*(1-p_k)$
$p_k$는 관심 영역 내에 클래스 k가 있는 훈련 예의 수를 나타낸다.

※ 기준 정지
재귀적 이분법 절차는 훈련 데이터 트리의 하단으로 진행해 가는 동시에 언제 분기를 멈춰야 하는지 알아야 한다.
이때 가장 흔한 정지 절차는 각 말단 노드에 할당된 훈련 예의 수를 세어 가장 작은 값을 이용하는 것. 그 수가 일부 최솟값보다 작다면 분기를 멈춘다.

※ 가지치기
트리의 과적합을 줄이기 위해 가지치기를 해주어야 한다.
가장 빠르고 단순한 방법은 테스트셋을 이용해 트리 말단 노드를 하나씩 선택하고 제거하면서 발생하는 결과를 평가하는 것.
결과가 전체 테스트셋의 전체 비용 함숫값이 떨어지는 경우에만 해당 말단 노드 제거, 더이상 향상되지 않으면 가지치기 종료

1
2
3

from sklearn.tree import DecisionTreeRegressor
model = DecisionTreeRegressor()
model.fit(X, Y)
  • 핵심 하이퍼파라미터는 트리 모델의 최대 깊이로, 사이킷런에 max_depth로 나타낸다.
    적절한 값은 2~30

※ 장단점

  • CART는 해석하기 쉽고 복잡한 관계성을 학습하는 데 용이
  • 데이터 스케일링 필요 x
  • 가지치기를 사용하지 않으면 과적합되기 쉽다.
  • 일반적으로 앙상블 모델보다 안좋은 성능을 보인다.

4.1.8 앙상블 모델

앙상블 모델은 여러 분류기를 합쳐 개개의 분류기보다 성능이 더 좋은 메타 분류기를 만든다.

  • 배깅: 병렬적으로 여러 개의 모델을 훈련하는 앙상블 기법
  • 부스팅: 순차적으로 여러 개의 모델을 훈련하는 앙상블 기법

※ 랜덤 포레스트
랜덤 포레스트는 배깅 결정 트리가 변형된 것.

배깅 단계:

  1. 데이터셋에서 임의의 많은 샘플 데이터셋 선택
  2. 각 샘플 데이터셋으로 CART 모델 훈련
  3. 새로운 데이터 셋이 주어졌을 때, 각 모델의 평균 예측을 계산하고, 각 트리에서 얻은 예측을 모아 과반수 투표로 최종 결과 선정
  • CART와 같은 결정 트리의 문제는 Greedy 알고리즘을 사용하는 것인데 이로 인해 각 트리의 예측이 서로 높은 상관관계를 가지게 된다.
    → 앙상블 모델로 이러한 모델의 예측을 통합할 수 있고, 하위트리 예측의 상관관계가 낮아지는 방식으로 학습 알고리즘을 변경한다.
1
2
3
4
5
6
7
8
9

# 분류
from sklearn.ensemble import RandomForestClassifier
model = RandomForestClassifier()
model.fit(X, Y)

# 회귀
from sklearn.ensemble import RandomForestRegressor
model = RandomForestRegressor()
model.fit(X, Y)
  • 최대 특성 수(max_features)는 가장 중요한 하이퍼파라미터로 각 분기점에서 샘플링할 임의 특성의 수이다.
    입력 특성 수를 절반으로 나누거나 1~20의 정수 구간을 선택한다.
  • 평가자 수(n_estimators)는 트리 수를 나타낸다. 원칙적으로 모델이 더이상 향상되지 않을 때까지 증가시키며 10~1000의 로그 스케일이 적당하다.

※ 장단점

  • 우수한 성능, 확장성, 용이한 사용성
  • 유연하며 큰 데이터셋에도 적용할 수 있으며 과적합에 안정적이다.
  • 데이터 스케일링이 필요없고 비선형 관계 모델링 가능
  • 결과 해석이 어렵다.
  • 분류에 비해 회귀에서는 정확한 연속성 예측을 하지 못한다는 단점이 있다.

※ 엑스트라 트리
완전 임의 트리라고도 하는 엑스트라 트리는 랜덤 포레스트가 변형된 것이다.
→ 동일하게 임의 특성 하위셋을 사용하여 다중 트리를 생성하고 노드를 분할하지만 부모 노드를 두개의 동종 자식 노드로 변환하기 위해 최선의 분기를 선택하는 랜덤포레스트와는 달리 엑스트라 트리는 부모 노드를 두개의 임의 자식 노드로 변환하기 위해 임의 분기를 선택한다.

1
2
3
4
5
6
7
8
9

# 분류
from sklearn.ensemble import ExtraTreesClassifier
model = ExtraTreesClassifier()
model.fit(X, Y)

# 회귀  
from sklearn.ensemble import ExtraTreesRegressor
model = ExtraTreesRegressor()
model.fit(X, Y)

※ 어답티브 부스팅(에이다부스팅)
순차적 예측으로 후속 모델이 앞선 모델의 오류를 최소화하는 방식으로 진행한다는 기본 아이디어로 만들어진 부스팅 기법.

  1. 처음에는 모든 관찰에 대한 가중치를 동일하게 한다.
  2. 일부 데이터로 모델을 생성하고, 전체 데이터셋에 대해 예측한다. 예측값과 실젯값을 비교해 오차를 계산한다.
  3. 다음 모델에서는 잘못 예측한 데이터의 가중치를 높인다.
  4. 비용 함수가 더이상 변하지 않을 때까지 혹은 예측 횟수가 최대치에 도달할 때까지 이 과정을 반복한다.
1
2
3
4
5
6
7
8
9

# 분류
from sklearn.ensemble import AdaBoostClassifier
model = AdaBoostClassifier()
model.fit(X, Y)

# 회귀  
from sklearn.ensemble import AdaBoostRegressor
model = AdaBoostRegressor()
model.fit(X, Y)
  • 학습률(learning_rate)은 각 분류기의 기여도를 로그 스케일로 축소한다. 격자 탐색을 위한 값으로는 0.001,0.01,0.1이 적당
  • 예측 횟수(n_estimators)는 트리의 수를 나타낸다.

※ 장단점

  • 에이다부스트는 고도의 정확성을 보인다.
  • 데이터 스케일링이 필요없고 비선형 관계 모델링 가능
  • 에이다부스트를 훈련하는 데 많은 시간이 필요
  • 잡음 데이터와 이상치에 민감

※ 경사 부스팅 방법
경사 부스팅 방법(GBM)은 또 다른 부스팅 기술로 순차적으로 예측한다는 측면에서 에이다부스트와 유사하다.

  1. 일부 데이터로 모델을 구축. 이 모델을 이용해 전체 데이터셋에 대해 예측
  2. 오차함수를 사용하여 오차 계산
  3. 이전 단계의 오차를 목표 변수로 사용해 새로운 모델 생성. 목적은 오차를 최소화하는 최적의 데이터 분기를 찾는 것이다. 새로운 모델로 얻은 예측을 이전의 예측과 통합하고 이로부터 얻은 예측값을 실젯값과 비교해 오차 계산
  4. 비용 함수가 더이상 변하지 않거나 예측 횟수가 최대에 도달할 때까지 위의 과정 반복

→ 매번 예의 가중치를 튜닝하는 에이다부스트와 반대로, 경사 부스팅 방법은 이전 예측의 오차를 보정하는 방식으로 새로운 예측기를 적합화한다.

1
2
3
4
5
6
7
8
9

# 분류
from sklearn.ensemble import GradientBoostingClassifier
model = GradientBoostingClassifier()
model.fit(X, Y)

# 회귀
from sklearn.ensemble import GradientBoostingRegressor
model = GradientBoostingRegressor()
model.fit(X, Y)
  • 하이퍼파라미터는 에이다부스트와 비슷하다.

※ 장단점

  • 데이터 오류, 높은 상관관계 특성, 무관한 특성에 안정적
  • 랜덤 포레스트보다 과적합에 더 취약하다.

4.1.9 인공 신경망 모델

1
2
3
4
5
6
7
8
9

# 분류
from sklearn.neural_network import MLPClassifier
model = MLPClassifier()
model.fit(X, Y)

# 회귀
from sklearn.neural_network import MLPRegressor
model = MLPRegressor()
model.fit(X, Y)
  • 은닉층(hidden_layer_sizes)는 인공 신경망 구조에서 층과 노드 수를 나타낸다.
  • 활성화 함수(activation)은 은닉층의 활성화 함수를 나타낸다.

※ 심층 신경망
은닉층이 하나 이상 있는 인공 신경망을 심층 신경망이라고 한다.

※ 장단점

  • 변수 간의 비선형 관계를 잘 나타낸다.
  • 문제 해결에 적합한 구조/알고리즘을 선택하기 어렵다.
  • 많은 연산이 필요해 훈련하는 데 시간이 많이 걸린다.

4.2 모델 성능

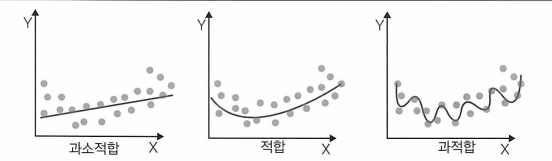
4.2.1 과적합과 과소적합

과적합은 모델이 훈련 데이터를 과도하게 학습할 때 발생, 과소적합은 모델이 데이터의 중요한 흐름을 파악할 수 있을 만큼 복잡하지 않은 경우에 발생한다.

image1.png

과적합을 방지하는 두 가지 방법

  1. 훈련 데이터 늘리기
    훈련 데이터가 많을수록 한 샘플에서 학습할 양이 많아지므로 과적합을 줄일 수 있다.
  2. 규제
    모델이 하나의 특성에 지나치게 많은 표현력을 보이거나 특성이 너무 많을 경우에 비용 함수에 패널티를 준다.

4.2.2 교차 검증

데이터가 적은 경우에 데이터를 한번 혹은 여러번 분할해서 검증셋으로 한번씩 사용하는 것.

훈련 데이터를 임의로 k등분한 후 k-1겹의 데이터로 모델을 훈련하고 k번째 겹으로 성능을 평가. 이후에는 다른 겹의 데이터로 모델을 훈련하고 성능을 평가하면서 해당 과정을 k번 반복하여 결과 점수의 평균을 구한다.

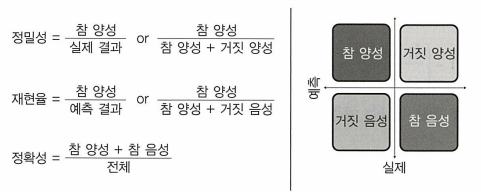
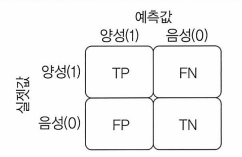
4.2.3 평가 메트릭

image1.png

  • 평균제곱오차에 제곱근을 취하면 출력 변수가 같은 측정단위로 변환되어 설명하고 제시하는 데 유용해진다. → 평균 제곱근 오차(RMSE)라고 한다.
  • 조정 제곱 오차
    $R^2_{adj} = 1 - \left[ \frac{(1 - R^2)(n - 1)}{n - k - 1} \right]$
    명 변수의 개수와 샘플 크기를 고려하여 보정한 값

※ 분류
image1.png

  • ROC 곡선아래영역
    ROC 곡선아래영역(AUC)은 이진 분류 문제에 적합한 평가 메트릭이다.
    AUC가 클수록 모델이 제대로 예측한다는 의미, AUC가 0.5라면 모델이 클래스를 구별하는 능력이 전혀 없다는 의미.

  • 혼동 행렬
    image1.png
    혼동 행렬은 두 개 이상의 분류를 갖는 모델의 정확성을 보여 주기에 용이.

4.3 모델 선택

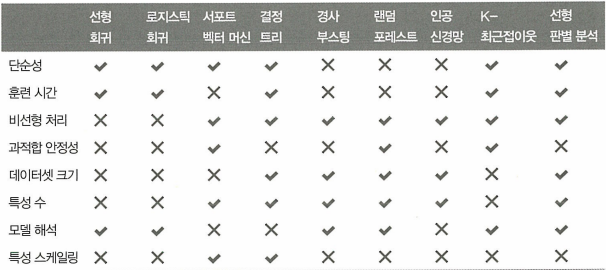
4.3.1 모델 선택 시 고려할 요소

  • 단순성
  • 훈련시간
  • 데이터의 비선형성 처리
  • 과적합에 대한 안정성
  • 데이터셋의 크기
  • 특성 수
  • 모델 해석
  • 특성 스케일링

image1.png

4.3.2 모델 균형

최종 모델을 선택할 때 예측 성능이 가장 중요한 목표라면 해석성이 낮은 모델을 선택하면 되지만 금융 분야의 경우 종종 해석성 중심 사례를 볼 수 있다.
→ 개인의 신용카드 신청을 허가하거나 거절하는 데 머신러닝 알고리즘을 사용한다고 하면 신청이 거절되어 고소나 법적 대응으로 이어질 때 금융기관은 어떻게 거절 결정을 내렸는지 설명해야 한다.
이때 인공신경망으로는 해석이 불가능하기 때문에 결정 트리 기반 모델이 더 적합하다.

KHUDA, Finance
KHUDA Quant ML
This post is licensed under CC BY 4.0 by the author.

Trending Tags

ML KHUDA Quant FBA_Quant