Review: Factor Momentum

해당 게시글은 Arnott et al.,(2023)의 “Factor Momentum” 논문을 리뷰한 글입니다. 본 게시물에서 인용한 논문 및 자료에 대한 상세 정보는 아래의 링크를 통해 확인하실 수 있습니다.
Arnott et al. (2023)

1. Introduction

기존에 모멘텀 팩터에 대한 성격을 보면, 산업은 주식 수익률에서 발견되는 것과 유사한 모멘텀을 보여줬지만, 주식 모멘텀과 달리 1개월 기간에서 모멘텀이 가장 강하게 나타나며, 이 기간 동안 개별 주식은 리버절 현상을 보인다.

또한 Lewellen (2002)는 주가순자산비율(B/M) 포트폴리오 수익률 또한 단기적으로 모멘텀 현상이 나타난다고 언급한다. → 팩터 또한 모멘텀 성질을 지닌다.

이 논문에서는 산업 모멘텀이 산업에 따라 생기는 현상이 아닌 각 산업이 어떤 팩터에 노출되어있는가에 관한 것이라는 것을 보인다. 또한 Lewellen (2002)의 연구 이외에도 다른 팩터들에 대한 모멘텀 수익도 비슷한 메커니즘을 통해 발생한다는 것을 보여주며, 횡단면 팩터 모멘텀 전략을 소개한다.

이 논문이 다른 연구와 가지는 차별점은,

1. Ehsani and Linnainmaa(2022) 의 지난 1년 수익률이 양이면 모두 롱, 음이면 모두 숏하는 팩터 모멘텀 전략(Time-Series Factor Momentum)
   → 양수라고 해서 모두 롱, 음수라고 해서 모두 숏 하는 것이 아닌 횡단면으로 동일한 팩터 수를 롱&숏 하는 전략

2. Jegadeesh and Titman(1993) 의 지난 1년 수익률을 기준으로 주식을 선택하는 개별 주식 모멘텀 전략
   → 개별 주식이 아닌 팩터 차원에서의 모멘텀 전략

따라서 이 논문에서 검증하고자 하는 가설은 “팩터, 산업, 개별 모멘텀 전략의 수익이 모두 동일한 근원에서 비롯된다.” 이다. 개별 주식 모멘텀 다음으로 가장 연구가 많이 된 분야가 산업 모멘텀이기 때문에, 이 논문에서는 산업 모멘텀의 방향을 입증하고자 한다.

산업 모멘텀을 사용하기 적합한 이유는, 팩터 로딩이 산업별로 시간에 따라 크게 달라질 수 있음을 보였기 때문. Fama-French 5 factor model 또한 모든 산업이 동일한 고정 팩터 로딩을 가진다고 가정할 때보다 산업별로 동적으로 로딩값이 달라진다고 가정햇을 때 시장 조정 산업 수익률 변동에 대한 설명력이 크게 증가함을 보였다.
→ 즉 팩터 로딩의 횡단면적 변동성, 시계열적 변동성을 모두 가지고 있는 것이 산업 모멘텀

결과적으로 팩터 모멘텀을 통제하면 모든 특성 모멘텀 전략의 알파가 0에 가까워지고 통계적 유의성이 사라진다는 것을 보인다.
반면, 팩터 모멘텀은 모든 특성 모멘텀 전략을 고려한 후에도 여전히 높은 수익성을 유지한다.
또한 산업 중립적(industry-neutral) 팩터를 사용한 팩터 모멘텀 또한 기존 팩터 모멘텀만큼의 수익을 보이며, 이 또한 산업 모멘텀을 포함한다는 것을 보인다.

이 논문은 “체계적 산업(systematic industries)”을 구성하여 팩터 로딩만의 변동으로 모든 산업 모멘텀이 발생함을 보인다. 롤링 윈도우 회귀 분석을 통해 각 산업의 팩터 로딩을 추정하고, 체계적 산업은 이러한 팩터 로딩에 의해 암시된 팩터 조합을 의미한다.
→ 팩터 로딩으로 인한 모멘텀은 유지하되, 산업 고유 충격은 전부 제거한 것이 체계적 산업

이렇게 만든 체계적 산업을 통해 분석한 결과, 팩터를 추가할수록 모멘텀이 커지는 것을 확인함. 또한 체계적 산업 모멘텀 이외에 나머지 산업 모멘텀의 양은 0으로 산업 모멘텀의 전부가 팩터 로딩으로 설명된다는 것을 시사함.

논문은 43개의 산업 중립 팩터로부터 주성분 팩터를 추출하고, 고유값이 높은 PC 팩터에서 대부분의 모멘텀이 집중되는 것을 보인다. 상위 5개 PC에서 발견된 팩터 모멘텀이 가장 높은 샤프비율을 가지며 하위 PC에서는 통계적으로 유의한 모멘텀이 없는 것으로 나타났다.

또한, 논문은 개별 주식이 단기 반전(리버절) 현상을 보인다면 도대체 팩터는 어떻게 모멘텀이 나타나는가? 에 대한 답을 낸다. 먼저 주식수익률을 체계적 요소(팩터) + 개별적 요소(주식 고유 충격)로 분리하고 상관관계를 분석한 결과 자기상관은 두 요소 모두 양이지만 교차 자기상관은 음의 관계로 나타났다.
따라서 주식 수익률의 단기 반전은 개별적 요소에 남아있기 때문에 팩터만으로 복제한 체계적 주식은 단기 모멘텀을 보인다.

2. Data

데이터는 NYSE, AMEX, Nasdaq에 상장된 주식의 월별 및 일별 CRSP 수익률 데이터를 사용한다.
또한 생존편향을 고려하여 상장폐지 수익률을 사용하며, 상장폐지 수익률이 없는 경우에는 Shumway and Warther(1999) 을 참고하여 NYSE, AMEX는 -30%, Nasdaq은 -55%를 적용한다.
회게 데이터는 Compustat을 활용하며 예견 편향을 방지하여 6개월 정보 지연을 준다. 1963년 7월부터 2021년 12월까지 진행되며 부채 발행 및 총 외부 자금 조달 팩터의 수익률은 1972년 7월부터 시작한다.

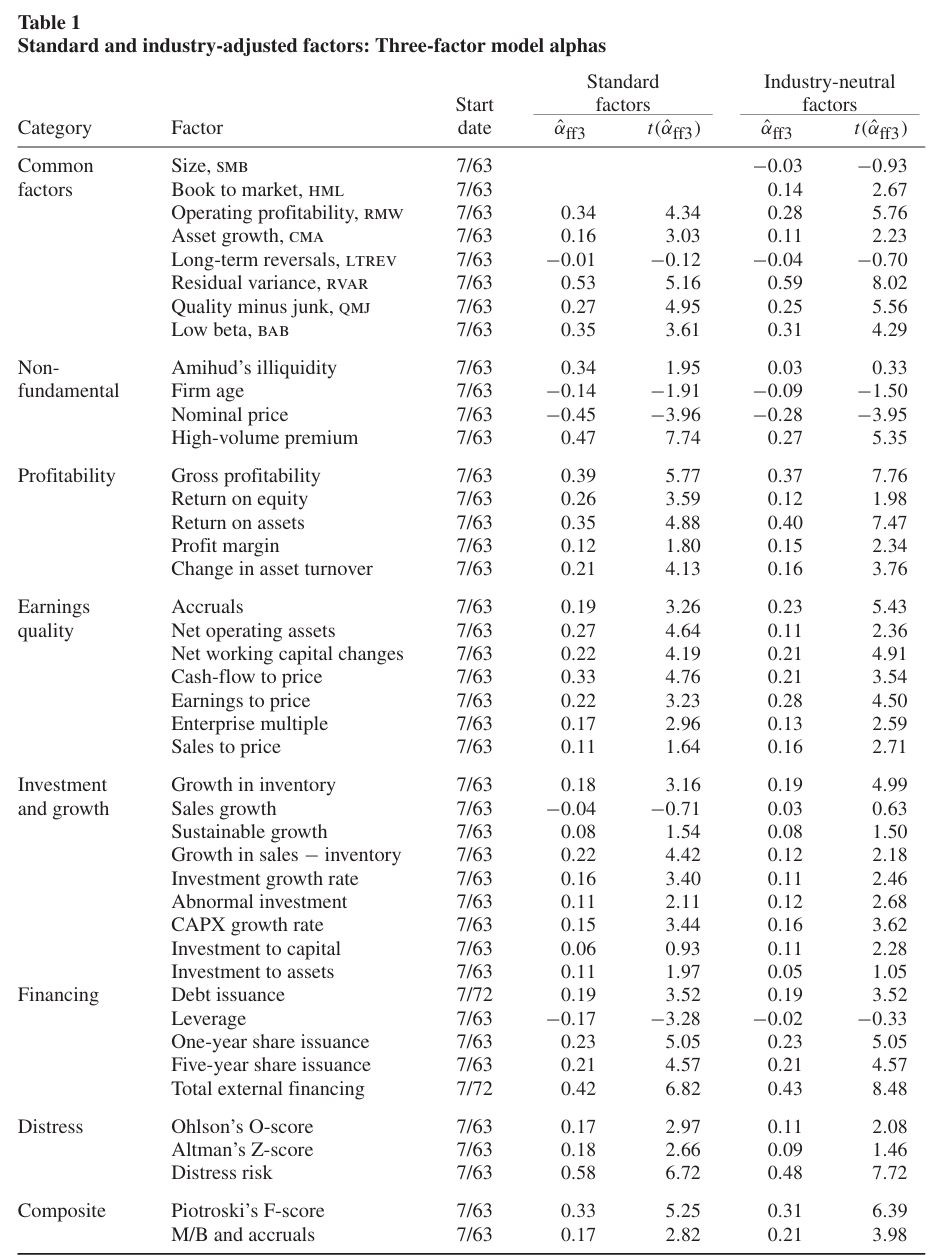
사용하는 팩터는 43개로, 팩터를 여덟 그룹으로 나누어준다.
→ Common factors, Non-fundamental, Profitability, Earnings quality, Investment and growth, Financing, Distress, Composite
팩터 모멘텀에 대해 연구하는 해당 논문 특성상 모멘텀 및 단기 리버절 팩터들은 제외하였으며 논문에서 산업 효과에 대해 분석하기 때문에 산업 집중도 팩터도 제외시킨다.

SMB 팩터 구성 과정은 Fama and French(1993)에서 진행한 절차와 동일하다. 다른 팩터들은 규모 중앙값 및 예측 변수의 30%, 40%, 30%를 기준으로 6개 포트폴리오를 분류하고 두개의 높은 포트폴리오에 대한 가치 가중 평균수익에서 두개의 낮은 포트폴리오에 대한 가치 가중 평균수익을 차감한다. 리밸런싱 주기는 각 팩터를 소개한 원 논문에서 진행한 주기를 적용한다.
또한 각 팩터에 대해 표준 버전과 산업 중립 버전을 구성한다.

마지막으로 원래 연구에서 지정한 방향대로 롱 포트폴리오를 설정하지만(ex. Value :long, Growth: short) 모멘텀 투자 관점에서는 어차피 과거 수익률이 높은 곳을 롱, 낮은 곳을 숏하기 때문에 부호 설정을 따로 진행하지 않는다.

3. Industry versus Factor Momentum

3.1. Industry momentum is a short-term effect

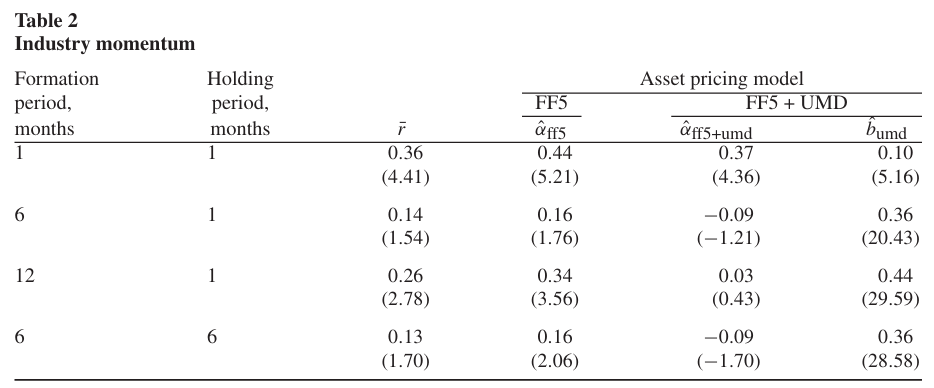
Table 2는 4가지 산업 모멘텀 전략에 대해 평균 월간 수익률 및 FF 5팩터 모델 알파를 보여준다.
각 전략은 수익률이 중간값 이상일 때 롱, 이하일 때 숏을 적용했다.

Moskowitz and Grinblatt(1999)의 20개 산업 분류 체계를 활용하였으며, 결과적으로 평균 수익률과 5팩터 모델에 대한 알파 모두 양의 값을 기록했다.
그러나 직전 한달 수익률을 기준으로 모멘텀을 형성하고, 리밸런싱을 한달 주기로 하는 전략만이 FF 5 팩터 모델 + UMD(모멘텀)에 대한 유의미한 양의 알파를 기록했다.
→ 개별 주식 모멘텀은 단기 산업 모멘텀을 제외한 모든 산업 모멘텀을 포함한다.

따라서 이 논문에서는 이후 산업 모멘텀을 한달 이전 수익률 기준 및 월별 리밸런싱 전략을 지칭하는 데 사용한다.

3.2. Cross-sectional factor momentum

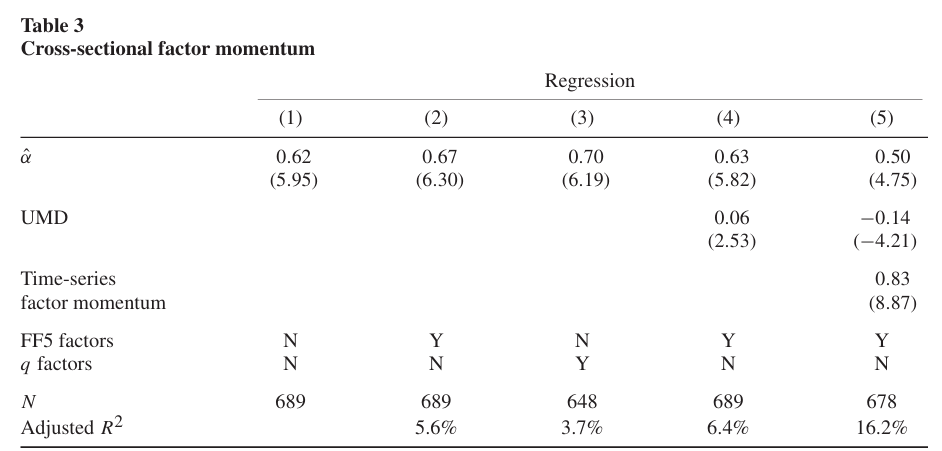
Table 3은 횡단면 팩터 모멘텀 전략의 월평균 수익률 및 알파를 나타낸다.

• 전략은 매월 리밸런싱되며, t-1(지난달) 시점에 중간값 이상의 수익을 낸 팩터에는 롱 포지션, 평균 이하 수익을 낸 팩터에는 숏 포지션을 취한다.
• 1열은 월평균 수익률을, 2열은 5팩터 모델에 대한 알파, 3열은 Zhang(2015)의 q-팩터 모형에 대한 알파, 4열은 5팩터모델 + UMD를 추가한 6팩터 모델에 대한 알파, 5열은 시계열 팩터 모멘텀(TSFM)을 추가한 7팩터 모델에 대한 알파를 나타낸다.
• 43개 팩터를 기준으로 하며, 팩터 모멘텀 전략은 월평균 0.62%의 수익을 기록한다.
• 5팩터 모델 뿐만 아니라 q-팩터 모델, UMD를 추가한 6팩터 모델 모두 횡단면 팩터 모멘텀의 수익성을 설명하지 못한다.
• 시계열 팩터 모멘텀과 횡단면 팩터 모멘텀은 서로 무관하다는 점을 알 수 있다(5열 참조). 이는 이전 연도에 양의 수익률을 기록한 팩터를 롱, 음의 수익률을 기록한 팩터를 숏하는 시계열 팩터 모멘텀과 전략적 차이가 존재하여 생기는 것으로 보인다.

Table 2, 3을 통해 산업 모멘텀과 횡단면 팩터 모멘텀이 모두 단기적인 효과이며, 5팩터 모형으로 통제했을 때 통계적 유의성이 더 커지는 것을 볼 수 있다.
(산업 모멘텀의 t-statistic: 4.41 → 5.21, 팩터 모멘텀의 t-statistic: 5.95 → 6.30)

3.3. Industry momentum, factor momentum, and momentum in industry-neutral factors

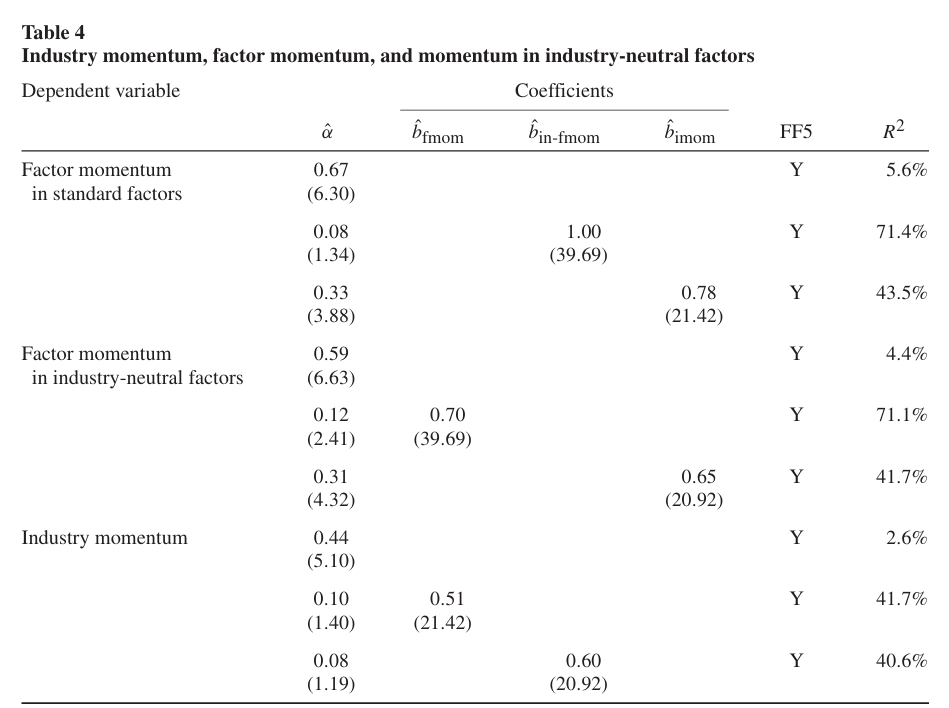
Table 4는 산업 모멘텀, 팩터 모멘텀, 산업 중립 팩터 모멘텀 간의 스패닝 회귀 추정치를 나타낸다.

• 종속변수를 각 모멘텀 전략의 수익률으로 한 시계열 회귀분석이며, 다른 모멘텀 전략을 하나씩 추가하여 만든 5팩터 모델으로 분석한다.
• 산업 중립 팩터 모멘텀과 표준 팩터 모멘텀이 서로 매우 유사하며, 산업 중립 팩터 모멘텀의 경우 월간 알파값이 약간 작은 반면 변동성 또한 낮게 나온다.
• 서로를 통제할 경우, 표준 팩터 모멘텀은 통계적으로 유의하지 않으나(t-statistic = 1.34), 산업 중립 팩터 모멘텀은 2.41의 t-statistic으로 유의성을 보인다.
• 산업 모멘텀을 통제할 경우, 표준 및 산업중립 팩터 모멘텀은 여전히 유의미한 알파를 보이는 반면 표준 및 산업중립 팩터 모멘텀을 통제할 경우 산업 모멘텀은 유의하지 않은 알파를 가진다.
• 설명력 또한 산업 모멘텀의 경우 2.6%의 설명력에서 팩터 모멘텀을 추가할 경우 40%까지 증가한다.
  → 팩터 모멘텀이 산업 모멘텀을 포함하며, 산업 모멘텀이 팩터 모멘텀의 원인이 될 수 없다.

3.4. Does factor momentum profit from persistent differences in factor premiums?

모멘텀은 과거 수익률이 좋았던, 즉 지속적으로 높은 기대수익률을 가지는 자산에 투자하는 전략이기 때문에 모멘텀 현상을 보이지 않아도 유의미한 수익을 거둘 수 있다. 따라서 이 논문에서는 팩터 모멘텀이 단순히 수익이 좋았던 팩터들을 들고 있었기 때문에 유의미한 수익을 거둔 것이 아니라는 것을 이 섹션에서 보이고자 한다.

Table 5에서는 대안적인 팩터 모멘텀 전략에 대한 결과를 나타낸다.

• FF 5 팩터 모델의 다섯가지 팩터만을 거래 대상으로 하고, 수익률이 중간값 이상인 두 팩터를 롱, 중간값 이하인 두 팩터를 숏한다.

이때 1열의 결과를 통해 이 팩터 모멘텀 전략이 66bp만큼의 유의미한 평균 월별 수익률을 가짐을 볼 수 있다.
→ 그러나? Conrad and Kaul(1998)의 가설에 따르면, 이 전략은 지속적으로 높은 프리미엄을 가진 팩터 쪽으로 기울어져 있기 때문에 당연히 수익을 내는 것처럼 보일 수 있다(Unconditional factor tilt).

실제로 각 팩터의 평균 월별 수익률은 59bp(MKTRF), 20bp(SMB), 27bp(HML), 28bp(RMW), 27bp(CMA)로, 시장 팩터를 롱하고 사이즈 팩터를 숏하면 높은 수익을 거둘 수 있다. 이 전략을 5팩터에 대해 회귀분석하면 무조건적 편향이 사라지면서 알파는 정확히 0이 될 것.
그러나 2열의 결과를 보면, 유의했던 MKTRF(시장 수익률), CMA(투자) 팩터의 로딩이 반대의 부호를 가지고 있다. 팩터 모멘텀에 대한 전략의 알파 또한 76bp로 평균 수익률보다 높은 값으로 나타난다.

뿐만 아니라 Conrad-Kaul 가설에 대응하는 또다른 접근법을 사용했는데, 이 접근법에서는 최소 5년간의 팩터 수익률이 필요하고 2달 전(t-2)까지의 모든 과거 데이터를 사용하여 팩터의 평균 프리미엄을 추정한 후, 이 평균을 팩터의 이전달(t-1) 수익에서 뺀 조정 팩터 수익률을 사용한다.
→ 왜 이렇게 하는가?: Conrad-Kaul 가설에 내포된 것은 프리미엄에 지속적이고 감지 가능한 차이가 존재한다는 것. 따라서 t-1 수익률에서 장기 평균을 제거함으로써 순수 모멘텀 효과를 보고자 함.

이 논문은 이러한 조정된 팩터 수익률을 기반으로 한 팩터 모멘텀 또한 유의미한 알파를 가지는 것을 확인하였다. Table 3에서의 기존 팩터 모멘텀의 알파값인 47bp(t-statistic: 4.32)에서 44bp(t-statistic: 4.1)으로 큰 차이가 없음을 보였다.

이는 이전달을 기준으로 하는 모멘텀 특성상 한달의 수익률만으로 장기 프리미엄을 설명하기에는 노이즈가 많기 때문에 편향이 발생하기 어렵고, 이전 문헌들에서 개별 주식 모멘텀에 대해 연구한 결과(Jegadeesh and Titman(2002)) 또한 유사했던 것으로 나타났다.

3.5. Is industry momentum about industries?

산업 모멘텀은 팩터 모멘텀으로부터 설명된다는 논리의 타당성을 검증하기 위해, 팩터 로딩의 변동이 유사하게 나타날 가능성이 있는 다른 주식 포트폴리오(대안 포트폴리오)를 만든다.

이 논문에서의 가설은,
“산업 모멘텀과 대안 포트폴리오의 모멘텀이 유사한 양을 가지고, 두 모멘텀 간 상관관계가 높다면 두 모멘텀은 동일한 근원(팩터 모멘텀)에서 발생한 것이다.”

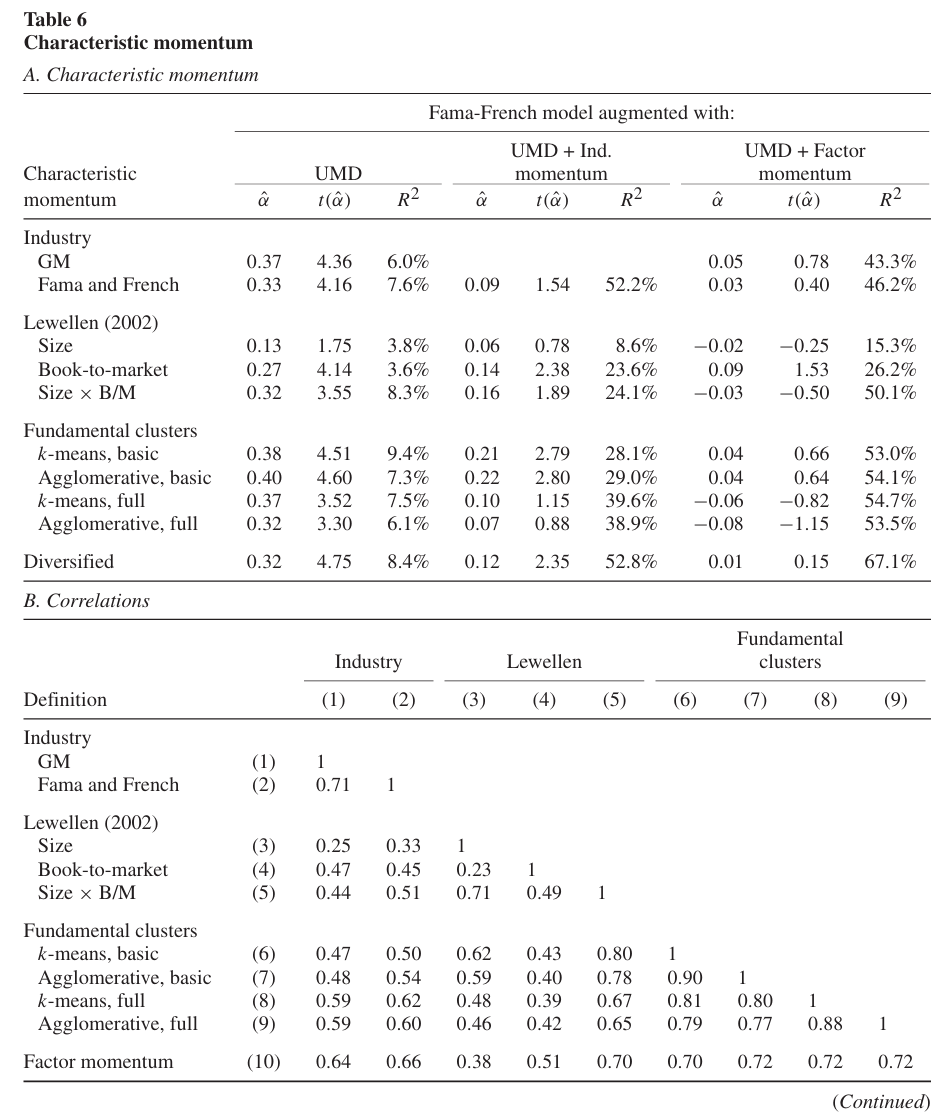
Table 6에서는 9세트의 포트폴리오에서의 횡단면 모멘텀 전략을 구성한 결과이다.

1-2: 산업(Industries). Moskowitz and Grinblatt의 20개 산업 외에도, Fama and French의 49개 산업 포트폴리오를 사용.
3-5: 사이즈, B/M 포트폴리오: Lewellen(2002)의 규모 및 장부가 대비 시장가치(Book-to-Market)의 10분위 포트폴리오와 각 비율에 따라 생성한 5*5 = 25개의 포트폴리오를 사용.
6-9: 펀더멘털 클러스터(Fundamental Clusters): FF 5팩터 모델의 4가지 특성(마켓 팩터 제외) 또는 다른 특성들(장기 반전효과, 잔차 분산, 퀄리티(Quality minus Junk; QMJ), 시장 베타)을 추가하여 NYSE 상장 주식을 25개의 클러스터로 분류. 기본 특성(4개) 클러스터는 연 1회 형성하며 전체 특성 집합(4개 특성에 다른 특성 추가한 버전)에 대해서는 매달 형성. 모든 특성은 정규화 작업을 거치며, K-means 알고리즘 및 agglomerative 알고리즘을 활용하여 클러스터 형성. → 기존의 특성 정렬 포트폴리오를 확장. 모든 특성 포트폴리오는 가치가중하여 수익률 산출.

이렇게 만들어진 포트폴리오의 모멘텀을 특성 모멘텀(characteristic momentum)이라고 부른다.

패널 A는 9개의 특성 모멘텀과 동일가중 포트폴리오(Diversified)에 대한 6팩터 모형 알파를 나타낸다.

• 10분위 사이즈 특성 모멘텀을 제외한 모든 특성 모멘텀 전략은 5팩터 + UMD 모델에 대한 알파가 유의하게 양의 값으로 나온다(t > 3.0).
• 특성 모멘텀의 동일가중 포트폴리오는 가장 높은 정보비율을 가진다(정보비율은 t값에 비례).
• 비산업 특성 모멘텀의 대부분은 산업 모멘텀을 6팩터 모델에 추가할 경우 통계적 유의성을 잃는다.
• 팩터 모멘텀을 추가한 6팩터 모델에 대한 알파는 모든 특성 모멘텀에서 통계적 유의성을 잃으며, 설명력($R^2$) 또한 증가한다.
  → 비산업 포트폴리오 또한 팩터 로딩의 변화로 인해 팩터 모멘텀을 상속받기 때문에 산업 모멘텀과 비슷한 패턴을 보인다.

패널 B는 각 특성 모멘텀 전략의 상관관계를 나타낸다.

• 모든 특성 모멘텀이 서로 강한 양의 상관관계를 가지며, 팩터 모멘텀과도 높은 상관관계를 가진다.

이는 산업 모멘텀이 실제로는 산업 자체에 관한 것이 아니라는 것을 시사한다.

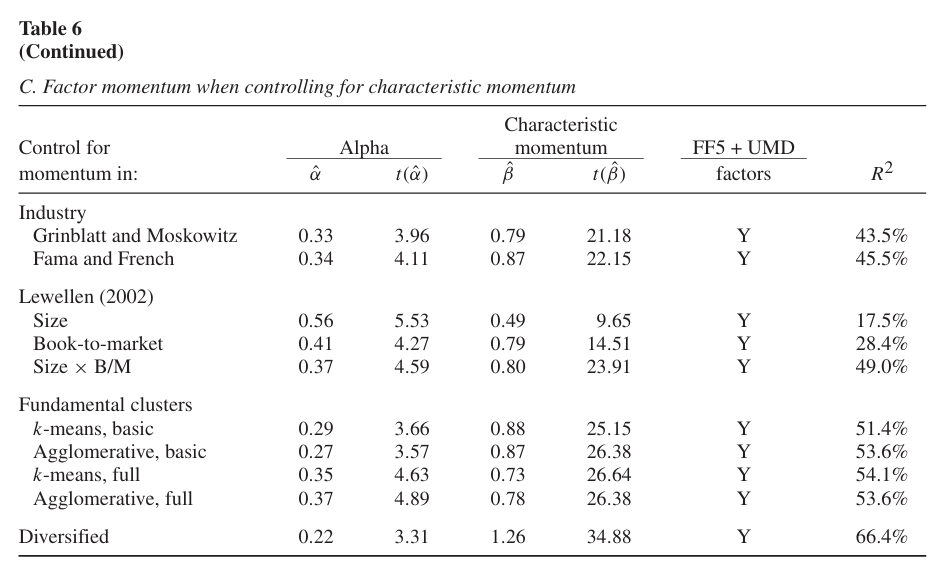
패널 C는 어떠한 특성 모멘텀도 팩터 모멘텀을 포함할 수 없음을 보여준다.

• 팩터 모멘텀을 6팩터 모델 + 특성 모멘텀 포트폴리오(Diversified)를 추가한 모델에 회귀분석한 결과 월별 알파값이 0.22로 유의하게 나타난다.

결국 Table 6의 결과를 통해 산업, 기타 특성, 팩터 모멘텀 모두 같은 메커니즘, 즉 팩터 및 팩터 로딩에 관한 것이며 팩터 모멘텀이 이러한 효과를 가장 명확하게 나타낸다는 것을 알 수 있다.

4. Transmission of Factor Momentum into the Cross-Section of Industries

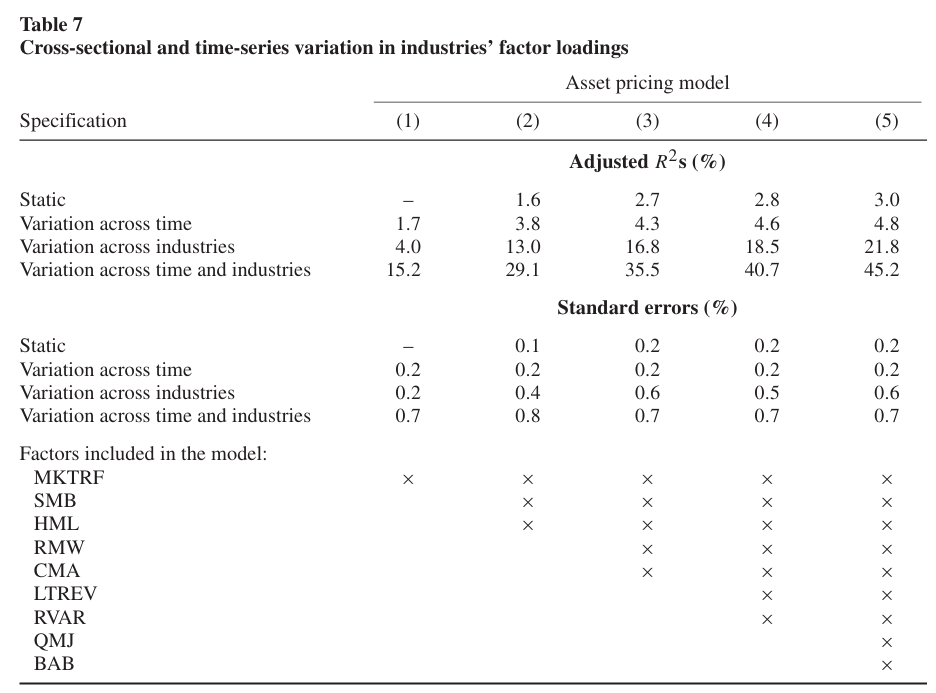
Table 7에서는 산업 간 변동성을 측정한다.
종속변수는 GM 20개 산업에 대한 일별 시장 조정 수익률이며, 독립변수는 마켓 팩터(CAPM)부터 시작해서 5팩터모델의 팩터 5개 + Table 1의 네가지 팩터(장기반전, 잔차 분산, QMJ, 마켓 베타) 를 포함한 9개 팩터의 일별 수익률이다.

static: 모든 산업이 동일한 팩터 로딩.
Variation across time: 산업 간에는 팩터 로딩이 같지만, 분기마다 로딩이 달라짐.
Variation across industries: 팩터 로딩이 산업별로 달라짐. 시간은 고정
Variation across time and industries: 팩터 로딩이 분기별로, 산업별로 달라짐.
→ 1963년 3분기부터 2021년 4분기까지의 분기 더미변수 및 산업 더미변수를 통해 회귀 진행.

결과를 보면, 시간변동만 허용한 경우 1.7%만큼의 설명력, 산업변동만 허용한 경우 4.0%의 설명력에서 둘 다 허용했을 때 15.2%의 설명력을 가진다. 이는 산업 수익률이 다양한 팩터의 로딩 변화로 인해 움직이며 시간에 따라서도 변동함을 알 수 있다.
→ 산업 모멘텀은 최근 잘나간 산업이 그자체로 영향을 준 것이 아닌, 최근 잘나간 산업이 잘나간 팩터에 더 많이 노출되어 있었기 때문이라는 것을 시사함.

5. Momentum in Systematic Industries

5.1. Defining industry-mimicking portfolios

이 섹션에서는 각 산업에 맞춰진 팩터 조합이 산업 모멘텀을 얼마나 설명할 수 있는지를 측정한다.

산업이 팩터 1,2,…,k에 대해 로딩 $\beta_1, \beta_2,…, \beta_k$ 를 가진다면, 이를 통해 산업 모방 포트폴리오를 구성할 수 있다.

체계적 산업(Systematic Industries): k팩터의 선형 결합으로 이루어진 산업 모방 포트폴리오
→ 실제 산업과 체계적 산업 간 차이를 잔여 산업이라고 한다.

5.2. Systematic industry momentum and spanning regressions

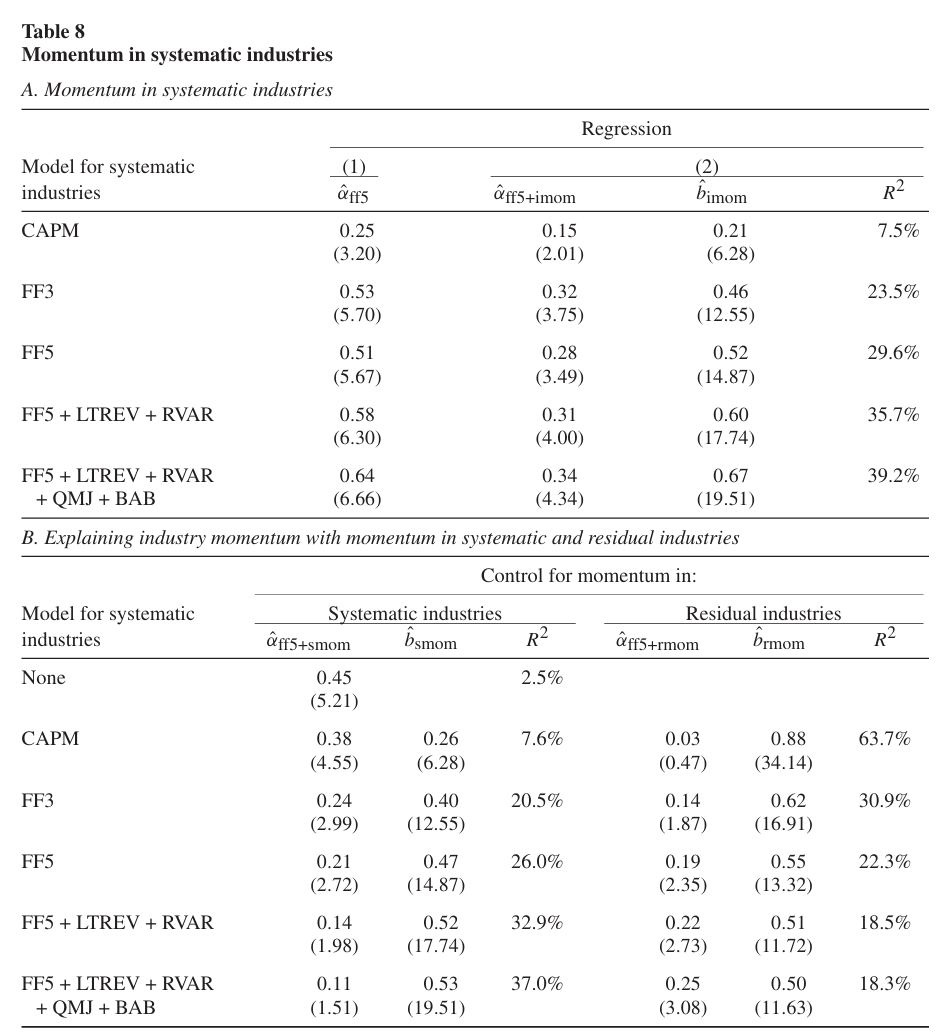
Table 8은 체계적 산업에서의 모멘텀 및 실제 산업 모멘텀 간의 관계를 측정한다.

• 각 산업의 팩터 로딩은 이전 3개월 동안의 일일 산업 및 팩터 수익률을 기준으로 추정.
• 체계적 산업 모멘텀은 기존 산업 모멘텀과 동일한 방식으로 구성된다. 이전 달 수익률을 기준으로 정렬한 후, 중앙값 이상 수익률을 가진 산업은 롱, 중앙값 이하 수익률을 가진 산업은 숏한다. 리밸런싱은 매달 이루어진다.

패널 A는 체계적 산업의 모멘텀에 대한 월별 알파를 나타낸다.
예를 들어, FF3 행의 경우 각 체계적 산업은 FF3에 해당하는 3개의 팩터의 조합으로 구성되며 산업 20개에 대해 롱숏 포트폴리오를 구성한다.

• 체계적 산업 모멘텀은 더 많은 팩터 조합으로 이루어질수록 강해진다. CAPM 팩터 기준 월별 알파 25bp에서 9팩터 기준 월별 알파 64bp로 증가한다.
• 산업 모멘텀을 통제하더라도 9팩터 기준 체계적 산업 모멘텀은 유지된다.

패널 B는 FF 5팩터 모델 + 체계적 산업 모멘텀(smom)에서의 산업 모멘텀의 알파를 나타낸다.

• FF 3팩터 조합으로 이루어진 모멘텀 만으로도 산업 모멘텀의 상당 부분을 설명할 수 있다(t-statistic: 5.70 → 2.99).
• 체계적 산업 모멘텀이 강해짐에 따라 산업 모멘텀은 점점 줄어든다. 반면 모형의 설명력은 점점 증가한다.

패널 B의 두번째 열(Residual industries)에서는 체계적 산업 모멘텀이 아닌 잔여 산업 모멘텀을 통제한다.

• CAPM 기준으로는 잔여 산업 모멘텀을 통제할 때 산업 모멘텀에 대한 알파가 없고, 64%의 설명력을 보이기 때문에 산업과 잔여 산업 사이에 의미 있는 구분이 이루어지지 않는다.
• 그러나 팩터를 더 추가할수록 산업 모멘텀의 알파가 양의 값으로 통계적 유의성을 가진다.

→ 산업 모멘텀의 수익이 팩터 모멘텀의 수익과 동일한 원천에서 비롯됨을 시사

6. Momentum in Principal Component Factors

6.1. Momentum in high- and low-eigenvalue PC factors

경제 이론은 자산, 팩터, 특성 자체에는 의미가 없고 차익거래자가 감당해야 하는 체계적 위험만이 가격을 결정하기에 수익률 변동을 가장 잘 설명하는 팩터 조합을 찾는 것이 중요하다고 말한다.

Kozak, Nagel and Santosh(2018)는 팩터 집합에서 주성분 팩터를 추출하고 팩터 프리미엄이 가장 큰 고유값의 팩터 소수에 집중된다는 것을 보여준다.
이 논문에서도 동일한 방법을 사용하여 팩터 모멘텀을 검토한다.

Table 1에서 나열된 43개 산업 중립 팩터에서 1972년 7월부터 시작되는 2개의 팩터를 제외한 41개의 팩터를 사용하여 주성분을 추출한다. t월까지의 10년간의 일간 수익률을 사용하여 t월 및 t+1월의 수익률을 계산하며 모든 팩터를 10% 변동성으로 정규화한 후 고유값 순으로 정렬한다.

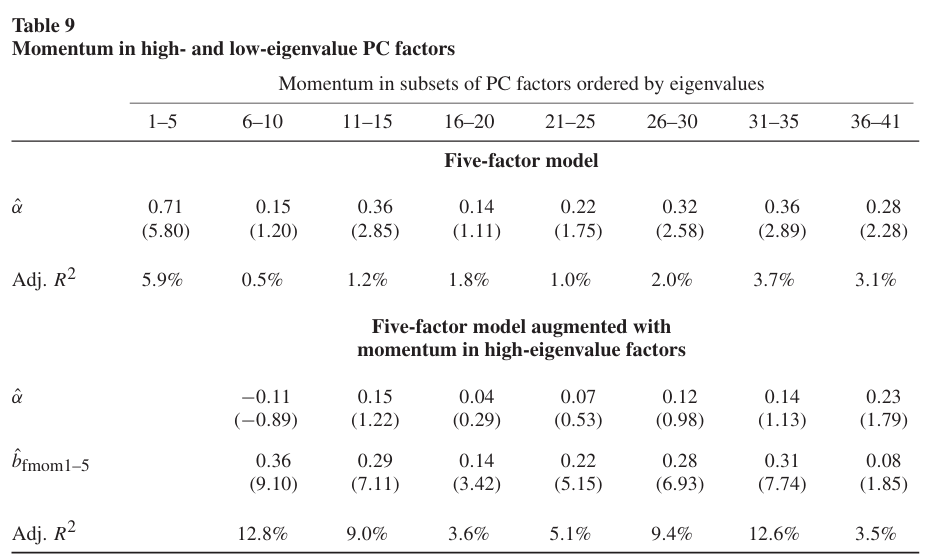
Table 9에서는 8개의 PC집합을 거래하는 모멘텀 전략의 성과를 나타낸다.

• 고유값이 가장 높은 PC1-5 집합에 대한 모멘텀의 경우 월 71bp의 통계적으로 유의한 알파값을 가짐.
• PC 11-15 모멘텀도 유의해 보이지만, 이는 PC1-5과의 상관관계로 인해 발생한 것일 수 있다(PCA 정의상 주성분 간에는 직교일 수 있어도 이를 대상으로 하는 모멘텀 전략이 직교라고 할 순 없기 때문).
• Table 9의 하단 부분에서 볼 수 있듯이 PC1-5 모멘텀을 통제할 경우 나머지 PC 모멘텀의 월별 알파가 통계적으로 유의하지 않으며, 이는 PC 팩터 모멘텀이 서로 상관관계가 있음을 시사한다.
  → 고유값이 높은 주성분만 포함해도 평균 수익률의 횡단면을 설명하기에 충분하다.

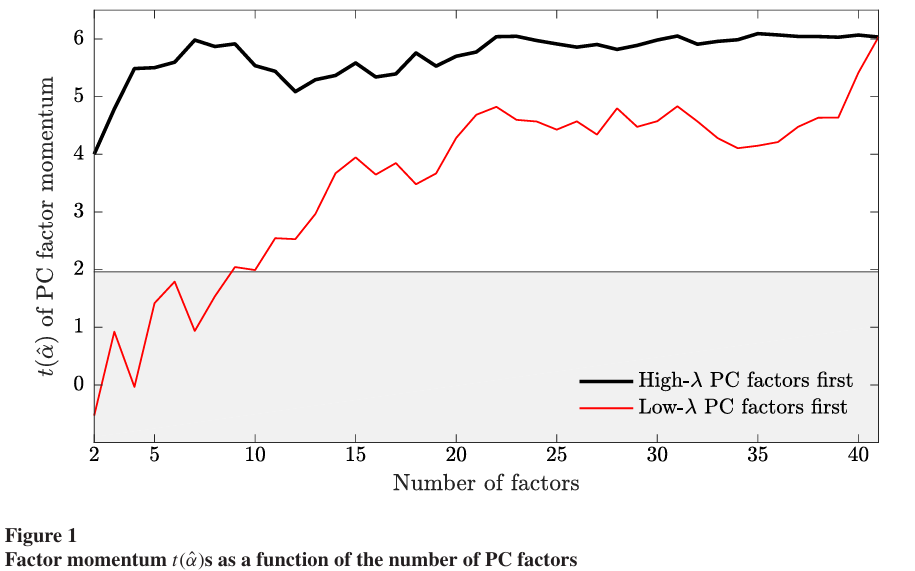
Figure 1은 높은 고유값에 대응하는 팩터와 낮은 고유값에 대응하는 팩터에서 발견되는 모멘텀의 양이 현저히 다르다는 것을 보여준다.
오로지 두개의 PC만을 거래 대상으로 시작하며 이때는 수익이 더 좋은 PC가 롱, 더 낮은 PC가 숏 대상이 된다.

• 검은색 선은 PC1-2(고유값 큰 순), 빨간색 선은 PC40-41(고유값 작은 순) 이며 순서대로 하나씩 PC를 증가시킨다.
• y축은 FF 5팩터 모형에 대한 각 팩터 모멘텀 전략의 월별 알파 t-statistic을 의미한다.
• 두 선이 매우 다른 수준에서 시작하며, 고유값이 큰 몇가지만을 대상으로 하는 전략이 41개의 PC를 전부 사용하는 전략 만큼 수익이 높으며, 고유값이 낮은 몇가지만을 대상으로 하는 전략보다는 월등히 높은 수익을 보인다.

6.2. Industry and other forms of characteristic momentum vis-à-vis high-eigenvalue PC factor momentum

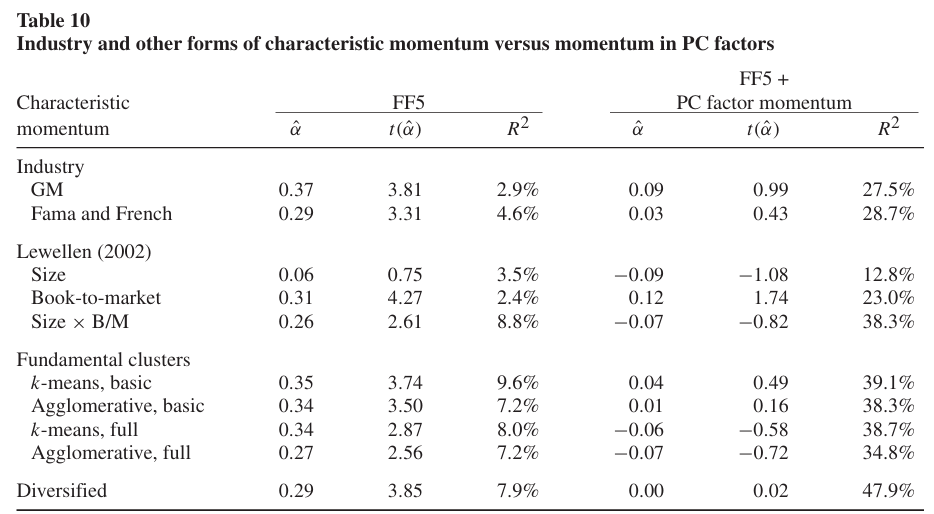
Table 10은 고유값이 높은 주성분 팩터(PC1-5)의 모멘텀이 모든 특성 모멘텀을 완전히 포함하고 있음을 보여준다.

• 모든 특성 모멘텀 전략들이 FF5 팩터 모델 + PC1-5 팩터 모멘텀을 추가한 모델에 대한 월별 알파가 통계적으로 유의하지 않은 것으로 나타난다.
• 다각화된 특성 모멘텀 또한 29bp의 월별 알파에서 0으로 감소하며, 통계적 유의성 또한 사라진다.
• 반면 낮은 고유값 PC 팩터 모멘텀을 포함한 5팩터 모형에 대한 특성 모멘텀의 월별 알파는 모두 유의미하게 남아 있다(인터넷 부록 Table A10 참조).

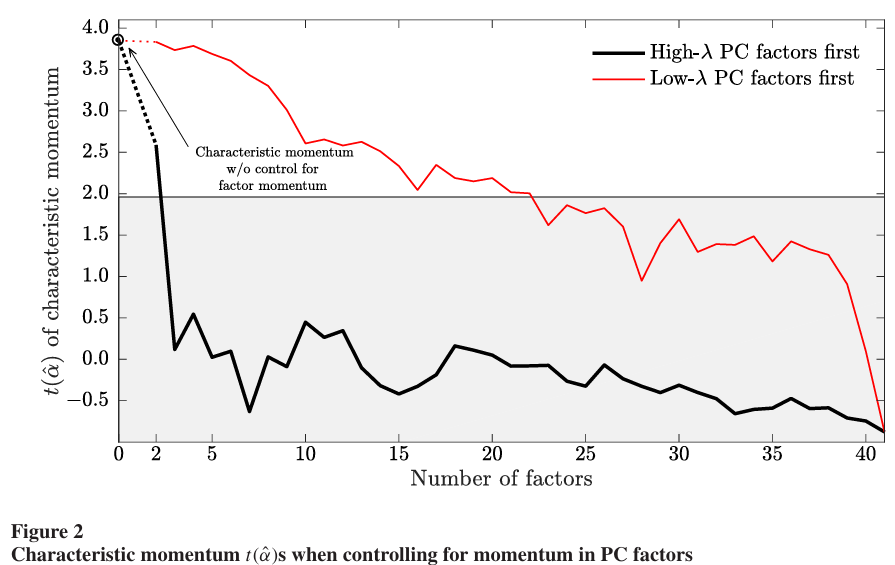
Figure 2는 특성 모멘텀과 PC 팩터 모멘텀 간의 연결을 보여준다. 구성 기법은 Figure 1에서와 동일하다.
→ Table 10에서의 결과와 마찬가지로 상위 PC 팩터 모멘텀을 통제할 경우 특성 모멘텀의 알파의 유의성이 급격히 떨어지는 반면, 하위 PC 팩터 모멘텀을 통제할 경우 특성 모멘텀의 알파 유의성이 오랫동안 유지되는 것을 볼 수 있다.

7. Reconciling Factor Momentum with Short-Term Reversals in Stock Returns

7.1. What are the sources of momentum profits and short-term reversals?

산업 및 팩터 모멘텀 전략으로 얻은 수익은 결국에는 주식 수익률의 어떠한 특징에서 비롯되어야 한다. → 산업과 팩터 모두 개별 주식의 포트폴리오이기 때문.

그러나 주식은 모멘텀이 아닌 단기 반전(short-term reversal)을 나타낸다.
따라서 이 섹션에서는 산업 및 팩터 모멘텀 전략과 개별 주식의 단기 반전에 대한 수익을 분해한다.

각 자산 i에 대한 가중치는 다음과 같이 산출한다.
$w_{i,t} = \frac{1}{N_t}(r_{i,t-1} - \bar r_{t-1})$
이때 $\bar r_{t-1}$ 는 시점 t의 횡단면에 있는 자산들의 횡단면 평균이다.

Lo-MacKinlay 접근법에 따르면 이러한 예상 수익률을 세 가지 항으로 분해한다.

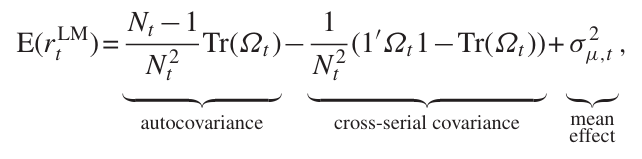
• $Ω_t = E_t[(r_{i,t}-\mu)(r_{i,t+1}-\mu)’]$ → 시점 t에서 자산 수익률의 자기공분산 행렬
• $\sigma^2_{\mu, t}$ → 시점 t의 평균 자산 수익률의 횡단면 분산

이 분해를 통해 횡단면 모멘텀 수익을 세가지 원천으로 구분한다.

1. 자산 수익률의 양의 자기공분산: 과거 자산 수익률이 미래 수익률이 높을 것을 나타냄
2. 음의 교차 시계열 공분산: 과거 자산 수익률이 다른 자산의 수익률이 낮을 것을 나타냄
3. 평균 수익률의 횡단면 분산: 일부 자산은 지속적으로 높거나 낮은 수익을 얻음
   → 각 성분은 1이 +, 2가 -, 3이 +일수록 모멘텀 전략에 도움이 됌.

먼저 각 자산의 수익률을 통해 자기공분산과 교차 시계열 공분산을 구한 후, 자산 수익률에서 두 항을 뺌으로써 평균 수익률의 횡단면 분산을 얻어낸다.
이때 개별 주식은 표본에 진입과 퇴출을 반복하기 때문에 생존편향을 방지하기 위해 월별로 분해를 따로 수행한 후 전체 샘플 기간동안 평균낸다.
부트스트랩을 통해 표본오차를 산출하며, 부트스트랩 반복마다 2000개의 주식을 랜덤 샘플링한다.
마지막으로 세개의 성분 모두 변동성을 10%로 스케일링해준다.

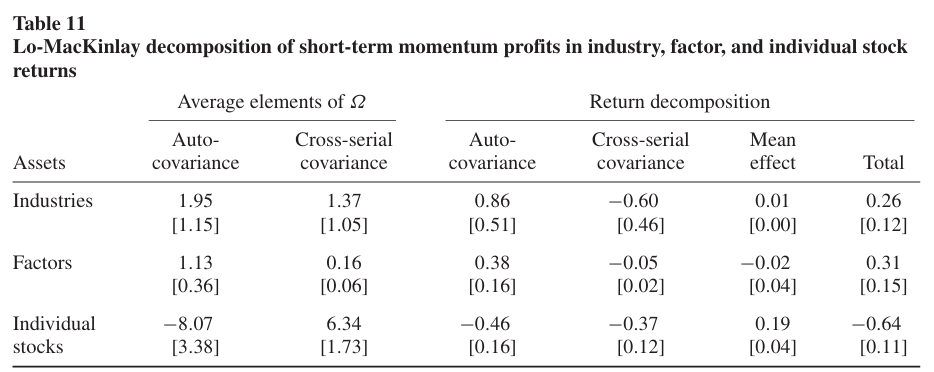
Table 11은 산업, 팩터, 개별 주식에 대한 자기공분산 및 교차 시계열 공분산을 나타낸다(괄호 안은 표준오차).

• 팩터와 산업은 모두 양의 자기상관 및 교차 시계열 상관을 나타낸다.
  → 산업의 자기공분산과 교차 시계열 공분산이 음수라고 보고한 Lewellen(2002)과 상반된 결과.
  이는 이전 1년동안의 수익을 기준으로 한 Lewellen(2002)와 다르게 이 논문에서는 직전 한달 수익을 기준으로 했기 때문.

• 개별 주식 수익률의 경우, 양의 교차 시계열 공분산을 가지지만 자기상관은 통계적으로 유의한 음의 값을 가진다.

• Return decomposition 결과에서는 팩터와 산업의 경우 양의 자기공분산 및 음의 교차 시계열 공분산을 가지는 반면, 개별주식은 자기공분산과 교차 시계열 공분산 모두 음의 값을 가진다.
  → 산업과 팩터 모멘텀의 수익의 근원은 긍정적인 단기 수익 자기상관임을 의미.
  → 개별 주식이 리버절 현상을 가지는 것은 음의 자기공분산의 영향임을 의미.
• 평균 효과는 전반적으로 미미한 영향을 줌.

7.2. Decomposing stock returns

개별 주식에서는 음의 자기상관이 관측된 반면 잘 분산된 포트폴리오(산업, 팩터)는 양의 자기상관이 관측되었다면 이는 개별 주식의 비체계적 요소로부터 발생한 것으로 볼 수 있다.
따라서 이 섹션에서는 주식 수익률을 체계적 요소와 특이 요소로 분해하여 리드-래그 효과를 측정한다.

주식 수익률은 5.1장에서와 동일한 접근법을 사용한다.
각 주식을 팩터 집합에 대해 회귀분석하며, t월의 체계적 요소는 추정된 베타와 팩터 수익률의 곱의 합으로 계산된다.
→ 투자자들은 t월까지 사용한 데이터로 베타를 추정한 후 t+1월에 체계적 요소에 대한 수익을 얻는 팩터 포트폴리오에 투자하거나 혹은 주식과 결합함으로써 비체계적 요소에 대한 수익을 얻을 수 있다.

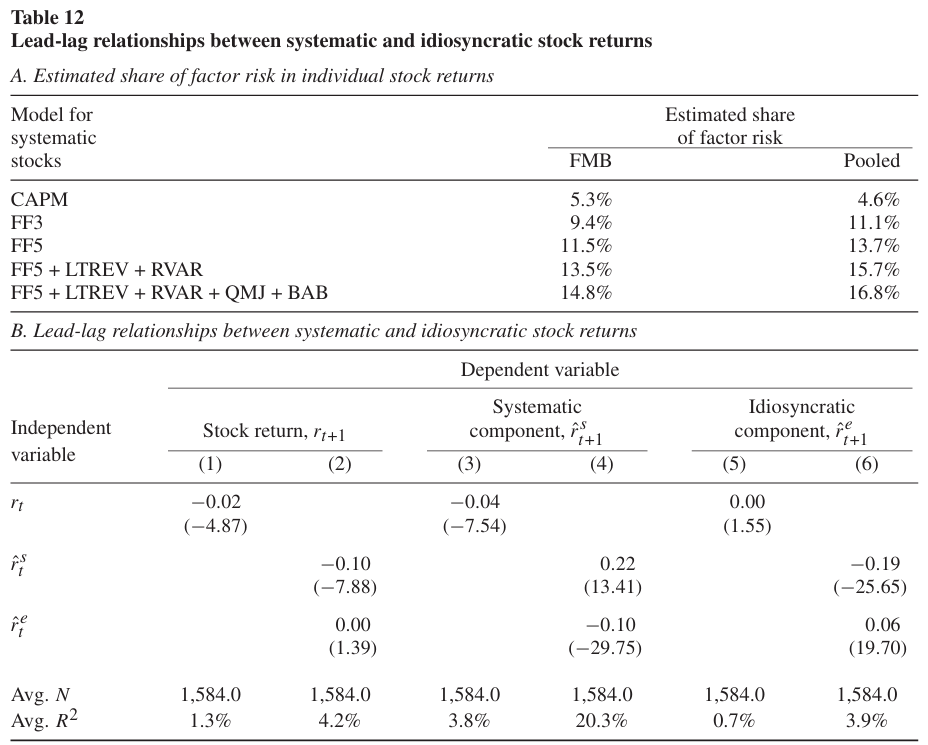
Table 12의 패널 A에서는 주식 수익률의 횡단면 분산에서 팩터 위험의 양을 측정한다.
종속변수: 주식의 실제 총 수익률
독립변수: 체계적 요소의 추정치(t+1월에 추정된 베타와 팩터 수익률의 곱의 합)

• 첫번째 열(FMB)은 월별 횡단면 회귀분석에서의 평균 adjusted $R^2$
• 두번째 열(Poolded)은 월 고정효과가 있는 pooled 회귀분석에서의 평균 adjusted $R^2$

결과적으로 두 회귀분석 방법에 대해 평균 adjusted $R^2$의 값이 유사하게 도출되었다.
팩터 수를 추가할수록 주식 수익률의 횡단면 변동 설명력이 높아지며, 9팩터 모델 기준 최대 17%의 설명력을 가진다. 이는 대부분의 주식 수익률의 변동이 비체게적 요소로부터 발생함을 시사한다.

패널 B에서는 체계적 및 개별 주식 수익률을 예측하는 횡단면 회귀분석의 추정치를 나타낸다.

• 1열의 결과에서는 주식 수익률이 리버절 현상을 나타낸다는 결과를 보여준다(t-statistic = -4.87).
• 2열 결과에서는 체계적 요소 또한 수익률을 부정적으로 예측함을 보여준다(t-statistic = -7.88).
• 주식 수익률의 체계적 요소 및 비체계적 요소는 양의 자기상관을 가지는 반면 서로에게는 음의 영향을 준다.

이로부터 얻을 수 있는 주식 수익률의 단기 리버절 현상의 원인은,

1. 만약 t월의 높은 주식 수익률이 체계적 요소로 인한 것이라면(즉 $\hat{r}^s_t$ 가 높다면), t+1월의 체계적 요소 수익률은 높을 것이고(자기상관이 양수이기 때문) 비체계적 요소 수익률은 낮을 것이다(음의 영향을 주기 때문). 따라서 패널 A에서 대부분의 주식 수익률 변동은 비체계적 요소로부터 이루어진다는 결과를 통해 t+1월의 주식 수익률은 음수가 된다(-0.10, t-statistic = -7.88).

2. 만약 t월의 높은 주식 수익률이 비체계적 요소로 인한 것이라면(즉 $\hat{r}^e_t$ 가 높다면), t+1월의 체계적 요소 수익률은 낮을 것이고(음의 영향을 주기 때문) 비체계적 요소 수익률은 높을 것이다(자기상관이 양수이기 때문). 그러나 비체계적 요소는 자기자신 보다는 체계적 요소와 더 큰 상관관계가 있기 때문에 전체 주식 수익률에 비체계적 요소가 더 많은 역할을 차지하더라도 서로 효과가 상쇄된다(0.00, t-statistic = 1.39).

따라서 주식 수익률의 단기 반전은 체계적 요소가 비체계적 요소를 음의 방향으로 예측하는 데에서 비롯된 것임을 나타낸다.

이러한 현상을 Lewellen의 행동적 설명과 결합하면, 어떠한 주식이 비슷한 특성을 가진 다른 주식과 과도하게 함께 움직이다가(뉴스 등과 같은 이유로) 어느순간 과도한 현상이 조정되면서 체계적 요소가 미래의 음의 비체계적 요소를 예측하는 것이라고 할 수 있다.

반면 팩터와 산업의 경우 잘 분산된 포트폴리오이기 때문에 이러한 개별 주식의 비체계적 요소에 영향을 받지 않아 단기 반전 현상이 일어나지 않는 것이다.
오로지 개별 주식에서 체계적 요소의 양의 자기상관만 남기 때문에 모멘텀 현상이 일어난다고 할 수 있다.

8. Conclusions

이 논문에서는 기존의 산업 모멘텀이 실제로는 팩터 모멘텀으로부터 설명된다는 것을 보여주며, 팩터 모멘텀 또한 단기적인 모멘텀 현상을 보인다는 것을 보여준다.
즉 팩터 모멘텀이 산업 모멘텀을 흡수하는 형태이며, 이를 4가지 방법으로 증명한다.

1. 산업 중립 팩터가 산업 모멘텀을 포함
2. 체계적 산업이 실제 산업 모멘텀과 유사
3. PCA를 통해 만든 상위 PC 팩터 모멘텀이 산업 모멘텀을 포함
4. 다양한 특성 모멘텀이 산업 모멘텀과 유사

또한 Lo-MacKinlay 접근법과 개별주식의 체계적 요소와 비체계적 요소의 분리에 따른 단기 반전 현상을 분석함으로써 팩터가 모멘텀을 보이는 원인을 보인다.

리뷰를 마치며

팩터 모멘텀에 대한 논문 중 하나인 Gupta and Kelly(2018)의 “Factor momentum everywhere”을 이전에 읽어본적이 있는데, 같은 팩터 모멘텀에 대한 논문임에도 보이고자 하는 방향성이 매우 다르다는 것을 느꼈다. 이 논문은 정말 체계적인 실험들을 진행했는데, 팩터 모델도 단순히 가장 대표적인 팩터모델만을 쓰는 것이 아닌 다양한 팩터 모델을 사용하였으며 실험 하나하나가 모두 저자가 주장하고자 하는 바를 뒷받침할 수 있는 근거로 작용되었다. 팩터 모멘텀에 관심을 가지고 있기도 해서 석사과정 중에 관련 연구를 진행해볼 생각이었는데 내가 생각했던 것보다 훨씬 더 구체적이고 엄밀한 실험들이 이루어져야겠다고 느꼈다.
이 논문에서는 팩터와 산업에서는 모멘텀이, 개별 주식에서는 리버절 현상이 일어난다고 언급했고, 이전에 읽었던 논문 또한 팩터에서 모멘텀 현상이 일어나는 것을 보였는데 단기 뿐만 아니라 중기, 중장기 등의 팩터 수익률에서는 한번도 리버절 현상이 일어나진 않는걸까 하는 생각이 들기도 했다. 팩터 리버절을 찾아낸다면 이는 팩터 모멘텀 전략의 성과 개선에도 큰 도움을 줄 수 있지 않을까?