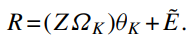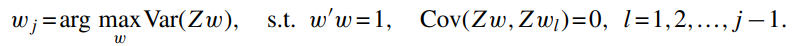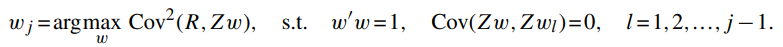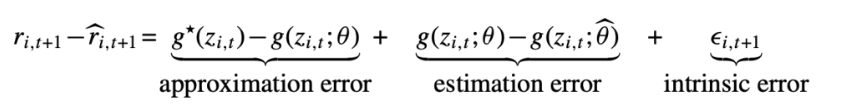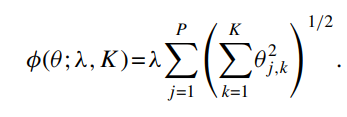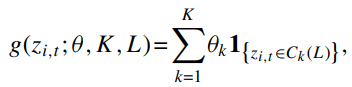Empricial Asset Pricing via Machine Learning 논문 요약

Empricial Asset Pricing via Machine Learning 논문 요약은 이미 FBA Quant학회 PO세션에서 HW12에 게시되어 있지만 이해가 잘 되지 않은 상황에서 급하게 요약한거라 차근차근 다시 요약을 진행해보려 한다.

SUMMARY: Empirical Asset Pricing via Machine Learning

Introduction

• 시장과 개별 주식의 risk premium을 측정하는 머신러닝 방법의 예측 정확성을 위한 벤치마크 세트 제공
• neural network를 활용하여 S&P 500 포트폴리오 전략은 buy-and-hold 전략보다 효율적(Sharpe ratio: 0.71 > 0.51)
• neural network를 기반으로 포지션을 취하는 value-weighted long-short decile spread 전략은 샤프비율 1.35
• 가장 유익한 예측 변수를 식별함으로써 어려운 risk premium 측정 문제 해결에 도움을 줌.
• 비선형 모델이 선형 모델보다 대부분 예측 성능이 좋고 그 중 신경망 모델(neural network)이 가장 좋은 예측 성능을 보임.
• 선형회귀, penalization이 있는 일반화된 선형 모델, PCR&PLS, 회귀 트리, 신경망 기법 활용하여 비교
• Shallow Learning이 Deep Learning보다 더 좋은 성능을 지님. → 딥러닝이 효율적인 비금융 환경과 비교했을 때 수익률 예측 문제의 데이터 양이 상대적으로 적고 신호 대 잡음비(signal-to-noise)가 작기 때문에 나타나는 것으로 판단

※ 벤치마크 세가지 특성(size, book-to-market, momemtum)을 반영하여 S&P500 포트폴리오 수익에 대한 바텀업 예측
→ 바텀업: 해당 변수가 좋은 팩터가 되는지 모르는 상황에서 영향력이 있는 팩터를 찾아나가는 방식

1. OLS $R^2$: -0.22(%)
2. generalized linear model $R^2$: 0.71(%)
3. Trees and neural network $R^2$: 1.08 ~ 1.8(%)

※ 사용 데이터
1957년부터 2016년까지 60년 동안 약 30,000종목의 개별 주식 데이터 사용.
각 주식에 대한 94개의 특성, 그리고 각 특성과 8개의 시계열 변수와의 상호작용, 74개의 산업 부문 더미 변수로 구성된 총 900개 이상의 baseline signal로 구성된 예측변수 집합 사용

가장 성공적인 예측 변수: 가격 추세(momentum, short-term rversal), 유동성(market value, dollar volume), 변동성(return volatility)

주식레벨보다 포트폴리오 레벨에서 더 뚜렷한 예측력을 보이는데 이는 데이터에서 시가총액이 낮고 유동성이 적은 일부 주식의 개별 수익률이 불규칙적으로 움직이기 때문. 포트폴리오로 수익률을 집계하면 노이즈가 대부분 상쇄되고 signal 강도가 높아져 예측 성능을 높이는데 효과적.

1. Methodology

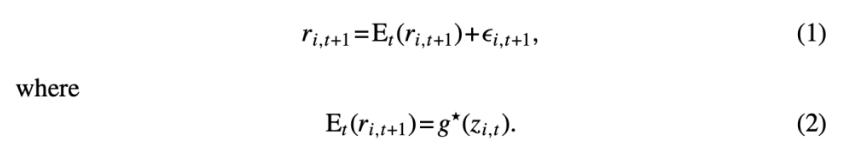
이 논문에서 가장 핵심이 되는 공식이라 할 수 있음. t+1시점의 자산 i의 실제 수익률을 t시점에서 예측한 값 $E_t(r_{i,t+1})$과 예측 오차$\epsilon_{i,t+1}$의 합으로 표현.
$g^*(z_{i,t})$: 자산 i의 수익률을 예측하는 데 사용되는 정보 집합 z의 예측 모델

1.1 Sample splitting and tuning via validation

※ Hyperparameter tuning

• 모델의 복잡도를 제어하는 중요한 요소로, 모델 성능에 큰 영향을 미침
• LASSO, elastic net의 penalization parameters, random forest의 random tree 수, 트리의 깊이 등이 포함
• 일반적으로 데이터를 세 개의 비연속적 시간 구간(Training Sample, Validation Sample, Testing Sample)으로 나누어 튜닝 파라미터를 선택하는 방식으로 접근
  → Training, Validation은 하이퍼파라미터 튜닝에 사용되지만 Testing은 튜닝에 사용되지 않으며 예측 성능을 평가하는 데 사용

1.2 Simple linear

1. standard least squares(L2)
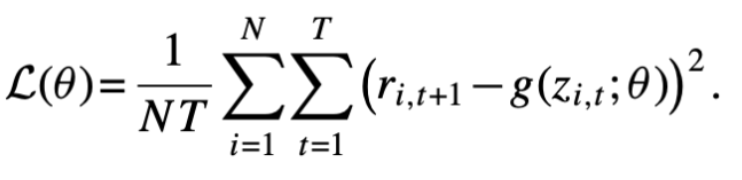
   • 목적함수를 최소화하면 풀링된 OLS estimator가 산출됨. L2 목적함수는 분석적인 추정치를 계산할 수 있어, 큰 컴퓨팅이 필요 없다는 장점이 있음.
2. weighted least square
   
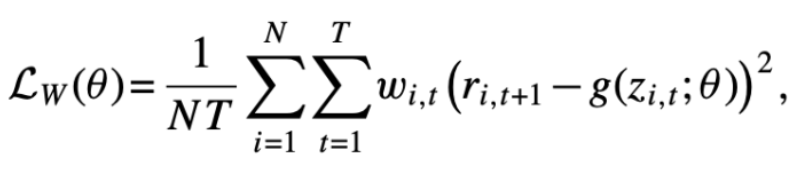
   • 경우에 따라 다음과 같이 가중 최소 제곱 목적함수로 대체할 수 있음.
   • 통계적 또는 경제적으로 더 많은 정보를 제공하는 관측치 쪽으로 추정치를 기울일 수 있음.
3. Huber robust objective function
   
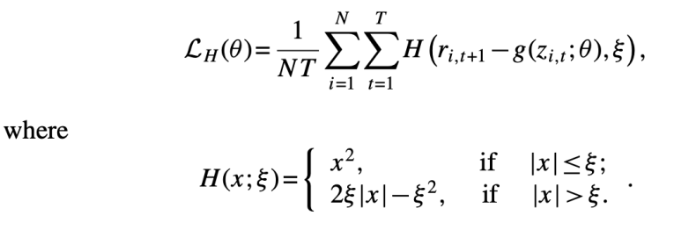
   • 극단적인 값들로 인한 heavy tails 문제를 보완해주는 목적함수. 극단적인 outlier가 있을 때 OLS보다 더 안정적으로 예측할 수 있음.

1.3 Penalized linear

• 단순 선형 모델은 많은 예측 변수가 있을 때 예측 실패 가능성이 큼.(Overfitting)
  → Overfitting을 방지하기 위해 모델의 성능을 일부러 약화시키는 Regularization 활용
  

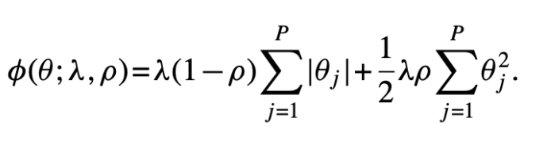
1.4 Dimension reduction: PCR and PLS

PCR분석: 주성분 분석(PCA)와 회귀 분석을 결합한 방법으로 다중공선성 문제를 해결하고 예측 변수를 줄이는데 활용

※ PCR 절차

1. 주성분 분석(PCA)에서 회귀변수를 예측 변수들 사이에서 공분산 구조를 가장 잘 보존하는 작은 선형 조합 세트로 결합
2. 주성분을 사용하여 종속 변수에 대한 예측 모델 생성
   → 낮은 분산 구성 요소 계수를 제로화하여 예측 문제를 정규화(regularization)

단점: 궁극적인 통계적 목표를 통합하지 못함. PCA는 데이터의 분산을 최대화하는 방향으로 주성분을 선택하지만 회귀 분석의 궁극적인 목표는 종속 변수에 대한 예측 정확도를 최대화하는 것. 따라서 PCA가 선택한 주성분이 회귀 모델의 예측 성능을 최적화하는 데 적합하지 않을 수 있음.
→ PLS는 종속변수를 고려하지 않고 PCA를 수행하는 PCR의 단점을 보완한 방법

• PCR과 PLS의 구현은 벡터화된 버전에서 시작
  $R = Z \theta + E$
  ($R:NT \times 1, Z: NT \times P, E: NT \times 1$)

($\Omega: P \times K$)

PCR

PLS

1.5 Generalized linear

근사 오차 (Approximation Error): 모델이 진정한 함수를 얼마나 잘 근사하는지 나타냄.
추정 오차 (Estimation Error): 모델 파라미터를 추정하는 과정에서 발생하는 오차
본질적 오차 (Intrinsic Error): 예측할 수 없는 본질적인 오차

일반화 선형 모델(GLM) 활용 → 원래의 예측 변수들에 비선형 변환을 도입하여 새로운 가법 항(additive terms)으로 추가. 이는 본질적으로 선형 모델에 비선형성을 도입하는 방식
이 논문에서는 GLM에 예측 변수들의 𝐾-항 스플라인 시리즈 확장을 추가하여 단순한 선형 형태를 적응시킴.

시리즈 확장은 모델 파라미터의 수를 빠르게 증가시키기 때문에, 자유도를 제어하기 위해 penalization 사용 → Group LASSO 활용
(시리즈 확장: 모델의 예측 변수를 고차항이나 비선형 함수로 확장하는 것)

1.6 Boosted regression trees and random forests

• regression trees는 다중 방향 예측 변수 상호작용을 통합하기 위한 인기있는 머신러닝 접근 방식
  K:잎
  L:깊이
  T:나무

Tree모델의 장점

1. 예측 변수의 단조 변환에 대해 불변성을 유지 → 트리 모델은 예측 변수의 순위(order)에만 의존하기 때문
2. 비선형성을 근사함.
3. 트리의 깊이가 깊어질수록 더 복잡한 변수 간 상호작용을 모델링할 수 있음
4. 범주형 데이터와 수치형 데이터를 동시에 처리할 수 있음.

단점: Overfit되기 쉬운 예측 방법 중 하나이기 때문에 regularization이 강하게 적용되어야 함.

1.7 Neural networks

• 복잡한 머신러닝 문제를 풀 때 선호되는 접근 방식
• 복잡성 때문에 해석하기 어렵고 고도로 매개변수화된 머신러닝 도구 중 하나

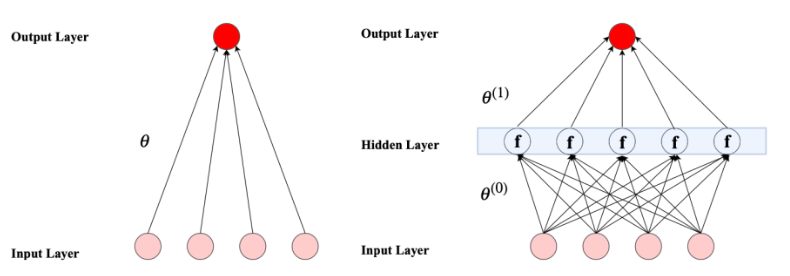
이 연구에서는 기존의 ‘feed-foward’에 초점을 맞춤.

• input layer
• hidden layer
• output layer

• 이전층에서 다음층으로 선형적으로 정보를 보내고 다음층에서 비선형 함수로 받은 정보를 변환하여 다시 결과를 선형적으로 합산하여 최종 출력

대 5개의 Hidden layer가 있는 아키텍쳐를 고려

1. 32개의 뉴런으로 구성된 단일 hidden layer
2. 32개와 16개의 뉴런으로 구성된 2개의 hidden layer
3. …
4. …
5. 32,16,8,4,2개의 뉴런으로 구성된 5개의 hidden layer

• 비선형 함수는 최근 연구들에서 널리 사용되는 함수 형태인 ReLU 선택 → 입력값이 0보다 크면 그 값을 그대로 반환하고 0보다 작으면 0을 반환하는 구조
  
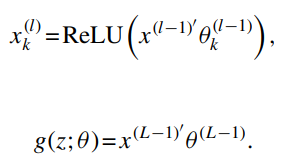
  $x_k^{(l)}$: l번째 층에서 k번째 뉴런의 출력 값

신경망 VS 트리 모델

• ‘greedy’최적화가 필요한 트리 기반 알고리즘과는 달리 신경망을 훈련하면 원칙적으로 최적화의 각 단계에서 모든 모델 파라미터를 공동으로 업데이트할 수 있으므로 트리에 비해 상당한 이점을 누릴 수 있음.(greedy 최적화: 전체 최적 솔루션을 찾기 위해 각 단계에서 가장 최적이라고 생각되는 결정을 내리면서 문제를 해결해 나가는 방식)
• 그러나 신경망의 높은 비선형성, non-convex한 성질, 매우 많은 매개변수화는 실행이 불가능해질 정도로 계산 집약적으로 만듦.
  → 일반적으로 해를 찾을 때 확률적 경사 하강(SGD)를 사용하여 신경망을 학습시키는데 이는 최적화 루틴의 가속화를 도와주는 반면 정확도가 낮아짐.

따라서 신경망의 regularization에는 더 많은 주의가 필요

• 학습률 축소(learning rate shrinkage) → SGD의 학습 속도를 제어
• 조기 중지(early stopping)
• 일괄 정규화(batch normalization)
• 앙상블(ensemble) → 신경망 학습 등 다른 기법을 동시에 사용하여 최적화 진행

1.8 Performance Evaluation

각 알고리즘 별 성과를 평가하기 위해 out-of-sample(test set) $R^2$ 계산(기존 $R^2$값과 다름)

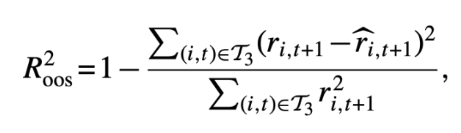
기존 $R^2$과 다른점은 분모 값이 어떤 값을 빼지 않은 초과 수익률을 제곱 합이라는 것
→ 기존 $R^2$을 사용하면 “좋은” 예측 성과에 대한 기준을 인위적으로 낮추게 됨.

방법론들을 짝을 지어 비교하기 위해 두 모델의 OOS 예측 정확도 차이에 대해 Diebold-Mariano 테스트 진행
※ Diebold-Mariano 테스트

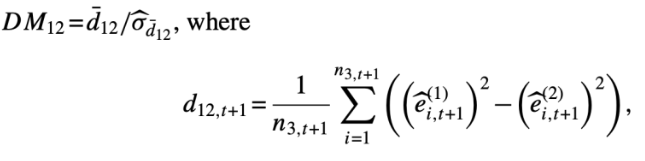
1.9 Variable importance and marginal relationships

변수 중요도 평가

1. 예측 변수 j의 모든 값을 0으로 설정하고 나머지 모델 추정치는 고정한 상태에서 $R^2$이 얼마나 감소되는지 확인하여 중요도 평가.
2. SSD 활용
   SSD의 j번째 변수의 중요도는 다음과 같이 정의됨.
   

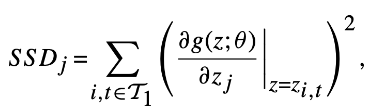
2. An Empirical Study of U.S. Equities

2.1 Data and the overarching model

NYSE, AMEX, NASDAQ에 상장된 모든 기업의 개별 주식 수익률을 CRSP로부터 얻고 무위험 수익률은 국채 금리로 계산.
가격과 종목코드에 관계없이 최대한 큰 주식 pool을 선택.

Welch and Goyal 연구에서의 변수 정의에 따라 dividend-price 비율, earnings-price-ratio, book-to-market, net equity expansion, T-bill rate, term spread, default spread, stock variance등 8가지 거시경제 예측 지수를 구성

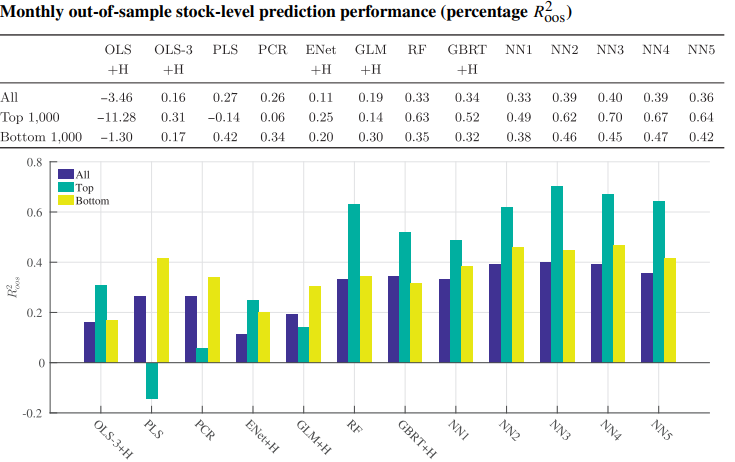
2.2 The cross-section of individual stocks

• 부스트 트리와 랜덤 포레스트는 각각 0.34(%), 0.33(%)의 적합도를 생성하며 PCR과 대등함.
• 가장 성능이 좋은 비선형 방법은 neural network. NN3의 경우 0.4(%)로 최고치 기록 → NN4, NN5모델이 더 개선되지 않는 것을 보아 학습의 이점이 제한적이라는 것을 보여줌
• 소형주 뿐만 아니라 대형주에서도 머신러닝 기법들이 높은 예측 성능을 보이고 있음. → 머신러닝 모델이 단순히 소형주의 유동성 부족으로 인한 비효율성만을 반영하는 것이 아니라는 것을 증명

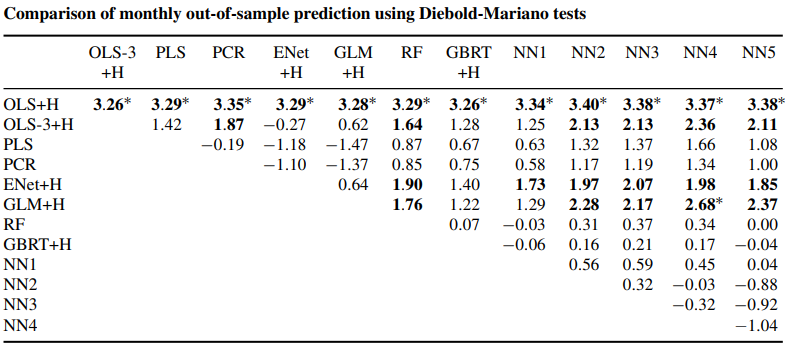
$\alpha = 0.05$으로 설정하고 t-statistic 값 비교

• 열 모델이 행 모델보다 우수한 성능을 가지는가? → 양의 statistic 값을 가지면 열 모델이 더 우수한 성능을 지닌 것
• 기본적인 선형 회귀 모델보다 비선형 모델들이 더 좋은 성능을 지님. 특히 NN3이 가장 좋은 성능을 보임.

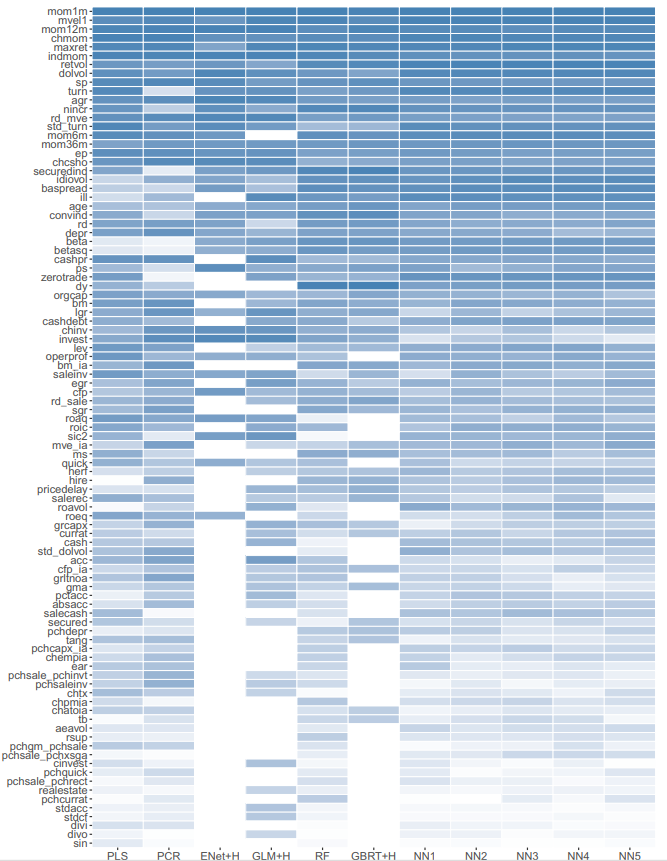
2.3 Which covariates matter?

• 중요도 측정을 사용하여 각 모델별로 예측 변수의 상대적 중요도 평가
• 각 predictor 모든 값을 0으로 설정했을 때의 R^2값의 감소를 계산하고 이를 각 predictor에 대한 단일 중요도 측정값으로 평균
• 모델 내 변수 중요도의 총합은 1

가장 영향력 있는 변수

1. 가격 추세(모멘텀, 최근 최대 수익률)
2. 유동성(로그시가총액, 거래대금)
3. 변동성(베타 제곱, 시장 베타)
4. PER, PSR 등

• SSD로 측정한 결과도 위와 비슷한 결과가 도출되었음

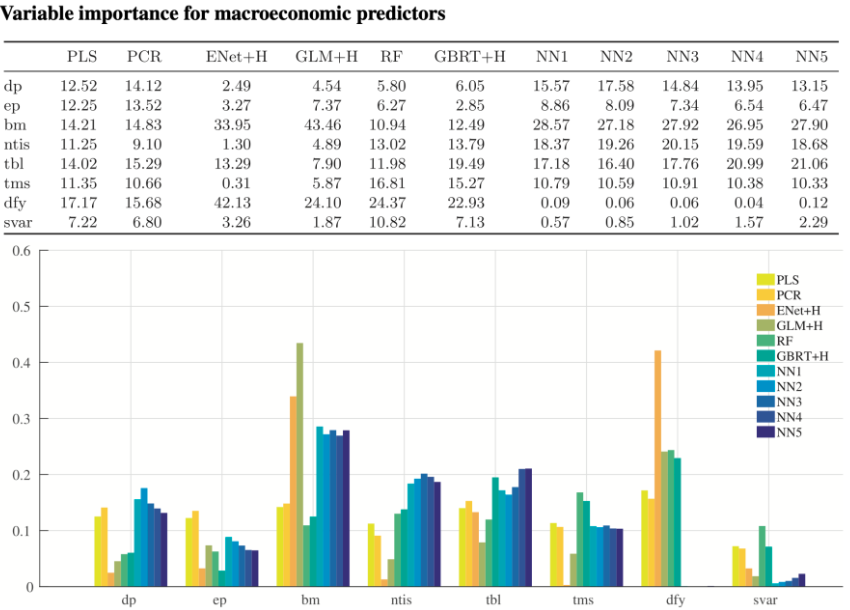
• 겨시경제 예측 변수에 대한 $R^2$ 중요도 측정값 비교
• PLS와 PCR은 다른 모델에 비해 전체적으로 비중을 비슷하게 두었음(변수 간 상관관계가 높기 때문)
• 비선형 방법은 선형 방법에 비해 term spread의 비중이 높음 (선형 모델에서는 term spread 변수가 무시됨)

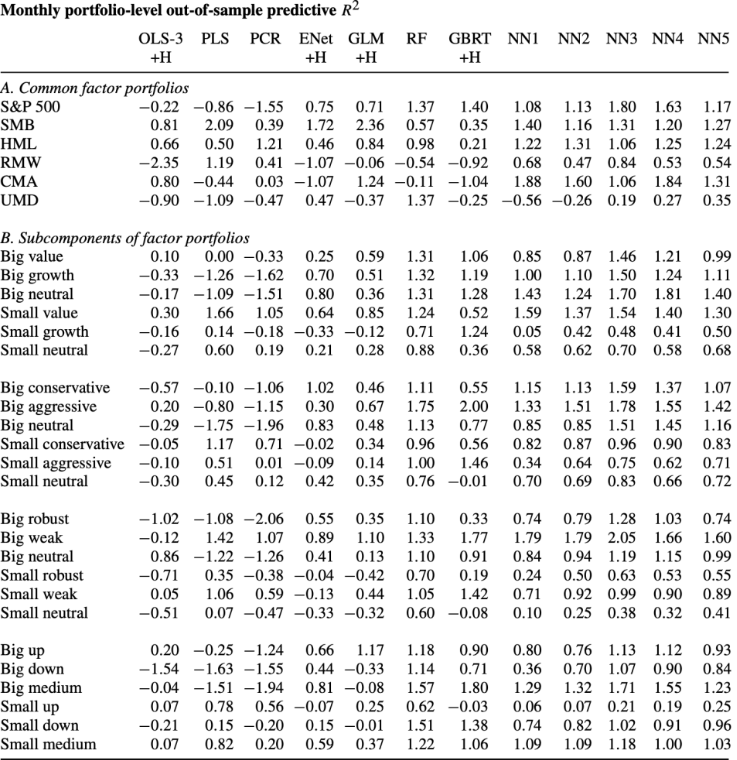
2.4 Portfolio forecasts

• 개별 주식 수익률이 아닌 포트폴리오의 총 수익률 예측 성능 비교
  
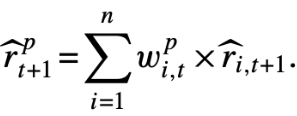
• 실증분석 금융 연구에서 가장 많이 쓰이는 30개의 포트폴리오(S&P500, Fama French-size, value, momentum 등)
• Fama-French 포트폴리오의 하위 구성 요소는 바텀업 예측 기반

• 선형회귀분석은 대부분의 변수가 양의 R^2을 만들어내지 못함.
• 비선형 모델이 확실하게 더 좋은 예측 성능을 보임
• 선형 모델은 바텀업 포트폴리오 수익률 예측에 대해 전반적으로 신뢰성이 떨어지지만 Small보다는 Big에서 더 나은 경향을 보임

$SR^* = \sqrt{\frac{SR^2 + R^2}{1 - R^2}}$

• 위 공식을 활용하여 포트폴리오 타이밍을 위해 머신러닝 예측을 활용하는 투자자의 연간 샤프비율 개선치 $SR^* - SR$를 구할 수 있음
• 다른 결과와 마찬가지로 비선형 모델을 기반으로 한 전략이 가장 좋은 성능을 보임.전반적으로 neural network가 우수

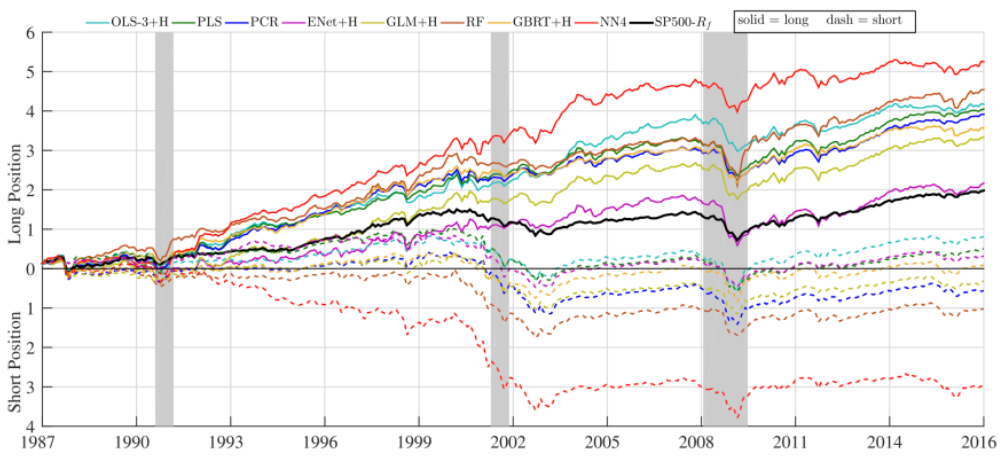
※ Machine Learning Portfolios

• 이미 지정된 포트폴리오의 수익률 예측이 아닌 머신러닝을 통해 새로운 포트폴리오 생성
• 10개의 주식 중 기대수익률이 가장 높은 주식 1개(decile 10) 매수 & 가장 낮은 주식 1개(decile 1) 매도 포트폴리오 구성
• value-weighted 방식을 사용하여 매월 포트폴리오 리밸런싱
• neural network 포트폴리오는 다른 대안들보다 샤프비율이 높을 뿐만 아니라 특히 equal-weight 포트폴리오의 경우에 상대적으로 하락폭이 작았음

• 위 결과를 바탕으로 모든 머신러닝 포트폴리오 예측을 결합하는 두가지 전략 구성
  1. 11개의 머신러닝 방법의 롱숏 포트폴리오를 동일한 가중치로 단순 평균 → equal-weighted 샤프 비율: 2.49, $R^2$:0.43(%) 으로 단일 방법보다 높은 수치 기록
  2. 해당 검증 샘플 동안 각 1년 테스트 샘플에 가장 적합한 머신러닝 모델을 선택하여 로테이션 구성
     → 30년간 NN3 11회, NN1 7회, GBRT 6회, NN2 5회, NN4 1회 선택. $R^2$은 가장 높지만 독립형 NN-4모델보다 샤프비율은 낮음

3. Conclusion

• ML 방법은 크고 유동성이 높은 주식과 포트폴리오 수익률 예측에서 큰 효과를 발휘
  → tree, NN이 다른 알고리즘들이 놓치는 비선형 상호작용을 포착하기 때문

• 다른 분야와 달리 Deep learning보다 Shallow learning의 성과가 좋은 이유 : asset pricing에서의 데이터 양의 부족, 낮은 signal-to-noise ratio(신호 대 잡음 비 율) 때문일 것으로 예상

• 모든 알고리즘에서 가장 강력한 예측 변수는 price trends와 관련된 predictors
  (return reversal, momentum : 수익률 반전, 모멘텀)

• 그 다음으로 강력한 예측 변수는 stock liquidity, stock volatility, valuation ratios 다.(주식 유동성, 주식 변동성, 평가 비율)