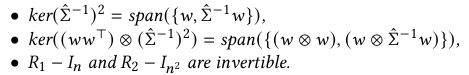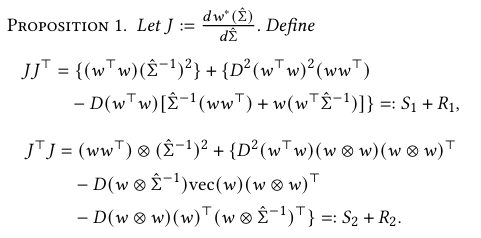Review: 'Estimating Covariance for Global Minimum Variance Portfolio: A Decision-Focused Learning Approach'
해당 게시글은 Kim et al.,(2025)의 “Estimating Covariance for Global Minimum Variance Portfolio: A Decision-Focused Learning Approach” 논문을 리뷰한 글입니다. 본 게시물에서 인용한 논문 및 자료에 대한 상세 정보는 아래의 링크를 통해 확인하실 수 있습니다.
Kim et al.,(2025)
1. Introduction
Markowtiz는 수익률 평균과 분산을 기반으로 한 mean-variance optimization(MVO)를 최초로 제시함으로써 현대 포트폴리오 이론을 확립하였다.
이러한 MVO에서 가장 중요한 부분은 기대수익률 및 공분산에 대한 파라미터 추정이다.
→ 모델의 민감도가 커서 기대수익률 추정에 약간의 오류만 존재해도 크게 영향을 받기 때문.
일반적으로 MVO의 파라미터 추정은 In-Sample 기간동안의 데이터를 기반으로 하는데 Out-of-Sample에서의 데이터와 분포가 달라질 경우 성과가 저조해질 가능성이 높아진다.
→ 동일가중 포트폴리오와 같은 단순 전략보다 성과가 낮아질 수 있음.
Global minimum-variance portfolio(GMVP)는 효율적 투자선에서 가장 낮은 위험을 가지는 포트폴리오로, 기대수익률을 사용하지 않기 때문에(공분산만 추정) MVO의 주요 문제인 기대수익률 추정오류에 영향을 받지 않는다(공분산은 비교적 기대수익률에 비해 예측 정확성이 높기 때문에 공분산 추정오류는 큰 영향을 주지 않음).
지금까지 공분산을 추정하고자 하는 다양한 방법들이 존재하는데, 대부분 Prediction-focused learning 프레임워크를 기반으로 MSE를 최소화하도록 하는 방법론을 사용한다.
그런데 과연 MSE를 최소화하는 모델이 최적의 투자 결정을 지원하는가? → ex. 두 자산의 기대수익률이 각각 A: 4%, B: 6%라고 가정하자. PFL 모델의 예측값이 A: 5.5%, B: 4.5% 라고 하고 DFL 모델 예측값이 A: 1%, B: 9% 라고 하면 실제 MSE는 PFL 모델이 더 낮음에도 불구하고 포트폴리오 성과는 DFL 모델으로 추정한 기대수익률 기반의 MVO가 더 좋을 것이다. 따라서 무조건 MSE를 낮추는게 최적의 투자 결정에 도움을 주는 것은 아님.
따라서 이 논문에서는 Decision-focused learning(DFL)을 활용하여 Lee et al.,(2024)의 “Anatomy of Machines for Markowitz: Decision-Focused Learning for Mean-Variance Portfolio Optimization.” 에서 진행한 MVO 이외에도 공분산을 추정하는 GMVP의 성과를 향상시키고자 한다.
※ DLinear?
시계열 데이터를 추세와 계절 성분으로 분해함으로써 선형 모델로 예측하는 방법론.
$x_t = Trend_t + Seasonal_t$
각 데이터의 Trend(추세), Seasonal(계절성) 성분을 각각 선형회귀하여 얻은 회귀계수를 기반으로 데이터를 예측 → $\hat y = \hat{Trend} + \hat{Seasonal}$
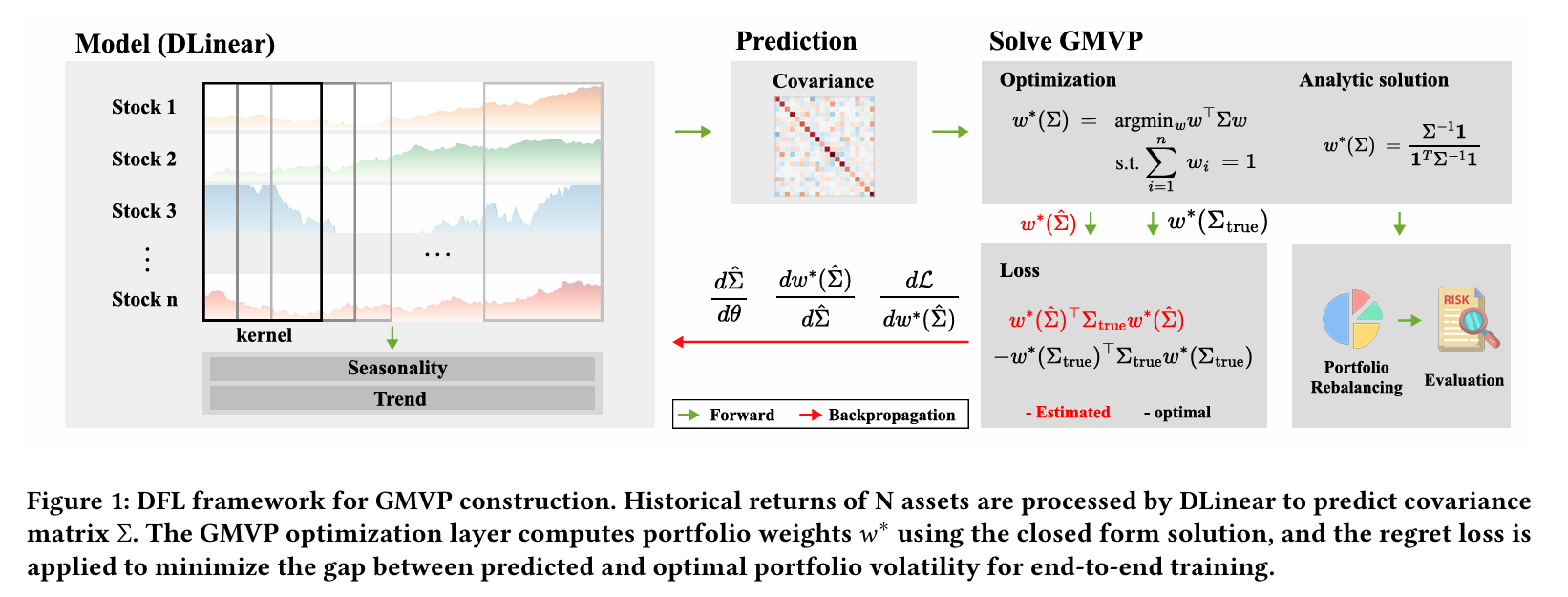
- DLinear 모델을 활용하여 공분산을 예측.
- 1번 과정에서 추정된 공분산을 기반으로 GMVP 최적화 수행.
- 2번 과정에서 산출된 각 자산의 가중치를 활용하여 Loss 함수 설정.
- Loss 값을 반영하여 다시 1번과정 반복
이를 통해 이 논문에서 보인 결과는,
- DFL이 GMVP 구성에서 PFL 기반 추정기를 능가하며, 기존 접근 방식은 한계를 존재한다는 것을 입증한다.
- DFL이 안정적인 자산 선정 기준을 제공하고, 시간에 따른 견고함을 보이며, 훈련 기간의 변동성과도 상관관계가 있고, GMVP 구성에 대한 의사결정 해석 가능성을 보인다.
2. Related Works
- 공분산 추정 관련
shrinkage estimators를 기반으로 한 샘플 공분산 행렬 추정 방법이 많이 발전된 바 있지만, 이 방법론은 Frobenius norm 아래에서 최적화되는데 이 때 포트폴리오 최적화 목표와는 직접적으로 일치하지 않기 때문에(공분산 추정 오류를 줄이는데에 초점) 위험 최소화에 관련된 공분산 구조를 포착하지 못할 가능성 존재.
→ 이러한 문제를 해결하기 위해 Bongiorno and Challet(2023), Mörstedt et al.,(2024) 는 Frobenius-norm loss를 포트폴리오 분산으로 대체하여 OOS 성능 향상을 보였음.
또다른 연구로는 베이지안 기법, 랜덤 매트릭스 등을 활용하여 공분산을 추정하였음.
→ 그러나 이러한 방법 모두 미리 지정된 파라미터 형태에 한정되어 표현력을 제한할 수 있음. 즉 이전 모델들은 “공분산을 추정한다”에 초줌을 두지만 DFL은 “공분산을 추정한다”가 아닌 “최적의 투자 의사결정을 내린다”에 초점을 둔다고 할 수 있다.
- Decision-Focused Learning 관련
최근 예측 중심 학습(PFL)을 대체하는 방법으로 등장했으며, 많은 연구자들이 모델 매개변수에 대한 최적화 계층의 그래디언트 표현을 도출함으로써 DFL에 대한 이론적 분석을 제공한다.
또한 최적화 계층이 미분 불가능할 경우, 서브그라디언트를 갖는 대체 손실(surrogate loss)을 제안하여 end-to-end 학습이 가능하도록 했다.
※ Surrogate Loss?
원래의 미분 불가능한 문제를 해결하기 위한 서브그라디언트가 정의된 대체 손실함수. 대표적으로는 부등식 제약식으로 인해 발생한 비미분성을 완화하기 위해 목적함수에 패널티를 주는 형태로 변환하여 최적화 맵 대신 서브그라디언트가 정의된 함수를 손실함수로 설정한다.
※ Subgradient?
미분은 불가능하나. 함수가 볼록성(convex)을 띄고 있어 해당 점에서의 지지선(점에서 그은 직선이 항상 함수 아래에 있는 선)이 존재하는 경우 서브그라디언트가 존재한다고 말한다. 대표적으로 $f(x) = |x|$ 가 있는데, x = 0에서 미분이 불가능하지만 $\partial f = [-1,1]$ 인 서브그라디언트가 존재한다.
일반적으로 경로 최적화, 통신 네트워크, 포트폴리오 최적화 등의 분야에 적용되어 왔는데,
금융 분야에서는 모델의 강건성을 향상시키거나 MVO에서 기대수익률을 추정할 때 주로 사용되었다.
3. Methodology
3.1. Notation and Problem Setup
N개의 자산과 T시점에 대한 자산 수익률 행렬을 $X \in \mathbb{R}^{T \times N}$ 라고 하면, $t_1$ 부터 $t_2$ 까지에 대한 부분행렬은 $X_{t_1:t_2} \in \mathbb{R}^{t_1-t_2+1 \times N}$
→ 이 시점간의 수익률에 대한 공분산 행렬: $\sum_{t_1:t_2}$
이때 in-sample 윈도우 기간 $\delta_{in}$, OOS 윈도우 기간 $\delta_{out}$ 에 대해 공분산 예측 모델은 다음과 같다.
$f_{\theta} : X_{t-\delta_{in}+1:t} ↦ \hat \sum_{t+1:t+\delta_{out}}$
이렇게 추정된 공분산을 기반으로 제약 없는 GMVP의 weight는 다음과 같이 구해진다.
$w^(\hat \sum) = \arg \min_w w^T \hat \sum w \quad s.t. \quad 1^Tw = 1 \ → w^(\hat \sum) = \frac{\hat \sum^{-1} 1}{1^T\hat \sum^{-1}1}$
3.2. Covariance Prediction model
이 논문에서는 공분산 추정 방법론으로 DLinear를 사용했다. 이는 단순한 구조에도 불구하고 시계열 문제에서 뛰어난 성능을 보여주었음.
이때 공분산 행렬은 대칭이고 양의 준정부호 행렬이기 때문에, DLinear를 통해 하삼각 행렬 L을 예측하고 이를 기반으로 공분산을 구성한다.
$\hat \sum = LL^T$
3.3. Decision-Focused Learning with Regret Loss
3.2 에서 공분산 행렬을 추정하면, 이를 기반으로 제약 없는 GMVP의 가중치 $w^*(\hat \sum)$ 을 계산한다.
이렇게 나온 가중치를 실제 그 시점에서의 공분산 값을 사용하여 포트폴리오 총 분산을 만들어준 후에, 실제 공분산을 기반으로 한 GMVP 가중치로 만든 포트폴리오 총 분산을 차감하면 regret loss가 만들어진다. 이는 의사 결정 품질을 평가하는데에 활용된다.
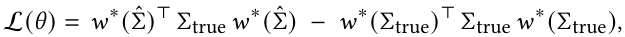
이때 $\sum_{true} = \sum_{t+1:t+\delta_{out}}$
이 loss function을 $\theta$ 에 대해 미분하여 경사하강법으로 업데이트한다.
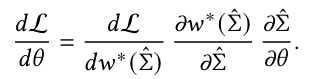
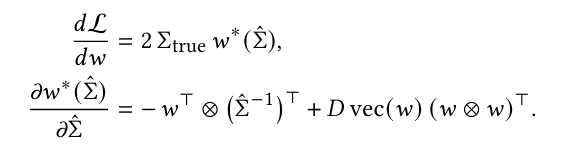
여기서 ⊗는 Kronecker product를 의미하며, $D = 1^T \hat \sum^{-1}1$ 이다.
→ 미분에 대한 자세한 과정은 ChatGPT 에서 확인할 수 있습니다.
마지막 항의 경우는 자동미분으로 계산됨.
4. Theoretical Analysis
이 섹션에서는 DFL 기반의 gradient가 왜 GMVP의 성과를 높이는지를 수리적으로 설명한다.
먼저 decision-aware gradient가 추정 공분산의 고유벡터 구조를 보존한다는 것을 증명한다.
이 경우 $JJ^T$ (가중치 공간) 와 $J^TJ$ (공분산 공간) 에 대해 동일한 고유값을 갖는 적어도 두개의 $\hat \sum$ -invariant한 특이 벡터(singular vector)가 존재하며, 각각 Assumption의 첫 번째 span, 두 번째 span에 속한다.
→ 즉, gradient가 고유벡터 방향을 바꾸지 않고 고유값만 바꾸기 때문에 안정적인 학습이 가능함. 또한 가중치와 공분산의 업데이트 모두 GMVP에 실제로 영향을 주는 구조로 업데이트됌.
이는 공분산을 업데이트 할 때 비중(포트폴리오 가중치)이 큰 자산의 공분산 업데이트에 초점을 두고 비중이 낮은 자산의 공분산 오차에는 초점을 두지 않는 형태로 진행된다.
→ risk contribution을 균형화하는 Risk-Parity 와 유사한 구조를 가짐.
5. Experiments
5.1. Experimental details
사용 자산군은 Kenneth R.French 데이터 라이브러리의 49개 산업 포트폴리오 및 2025년 4월 1일 기준 시가총액 상위 100개 S&P 500 주식을 선택한 S&P 100, 그리고 다우존스 30 지수를 사용한다.
각 자산군은 2010년 1월 1일 ~ 2024년 12월 31일까지의 일일 수익률을 통해 공분산 행렬을 추정하며, 수익률 데이터가 없거나 두 주식 간 상관계수가 0.95 이상인 주식은 제외한다.
데이터 구분은 학습, 검증, 테스트를 각각 6:2:2로 분할한다.
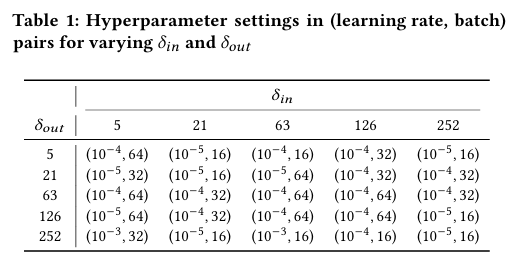
하이퍼파라미터는 그리드 서치를 활용하며 데이터 학습은 Adam optimizer, 모든 모델은 최대 50 에포크까지 학습, 7 에포크 동안 검증 손실이 개선되지 않으면 조기 종료 등을 사용한다.
공분산 추정에 활용하는 DLinear의 Kernel size(window 길이)는 max(5, min($\delta /3$ , 50))이며 hidden dimension은 128로 설정한다.
5.2. Results
DFL 접근법의 성능은 다음 벤치마크와 비교한다.
- EW: 동일가중 포트폴리오
- Historical: 수익률 샘플 공분산을 사용한 GMVP
- LW-D: Ledoit-Wolf 축소를 적용한 GMVP
- LW-CC: Ledoit-Wolf 상수 상관 축소를 적용한 GMVP
- OAS: Oracle Approximating Shrinkage 추정기를 적용한 GMVP
- PFL: MSE를 최소화하는 방향으로 DLinear 기반 공분산 예측한 GMVP(DFL과 Loss의 차이 존재)

Table 2는 테스트 기간동안의 연평균 변동성을 나타내고, 그림 2은 각 기간동안의 연평균 변동성 그래프이다.
- DFL 방법이 가장 우수한 변동성을 보이며, Frobenius norm 손실을 최적화하는 전통적 추정 방법은 포트폴리오 변동성을 낮추는 것과 직접적으로 연결되지 않기 때문에 성과가 좋지 못한 것을 알 수 있다.
- PFL은 EW와 유사한 성과를 보이는데, 이는 MSE 기반 공분산 예측이 사실상 균등 가중 할당을 유도할 수 있음을 나타낸다.
그림 4는 테스트 기간동안 49개 산업 데이터셋의 평균 섹터별 가중치를 나타낸다.
- PFL은 EW와 거의 일치하는 반면 다른 모델들은 뚜렷한 포지션 노출을 보인다.
→ 이는 MSE가 훈련 단계에서 공분산 행렬에 값이 큰 대각선에 대한 오류를 줄이는 것을 우선시하기 때문에 발생하며, 비대각선 요소가 과소적합되어 균일한 상관관계를 생성하게됨.
그림 5는 다양한 윈도우 조합에 대한 변동성을 나타낸다.
- OOS의 윈도우가 증가하면 DFL의 변동성이 커지며, 이는 장기 예측에서 더 큰 불확실성을 반영한다.
- In-Sample 윈도우의 변동에는 변동성 성능의 차이가 크게 존재하지 않는 것을 통해 강건성을 보인다.
5.3. Empirical properties of DFL
이 섹션에서는 근사 최적 포트폴리오(예측한 공분산으로 만든 포트폴리오)를 DFL이 어떻게 만들어내는지에 대해 특성을 분석한다.
이를 위해 정밀도 행렬의 순열을 분석한다.
→ GMVP의 w는 정밀도 행렬($\sum^{-1}$)이 직접적으로 결정하기 때문에 자산 순서를 의미있게 재정렬하여 분석
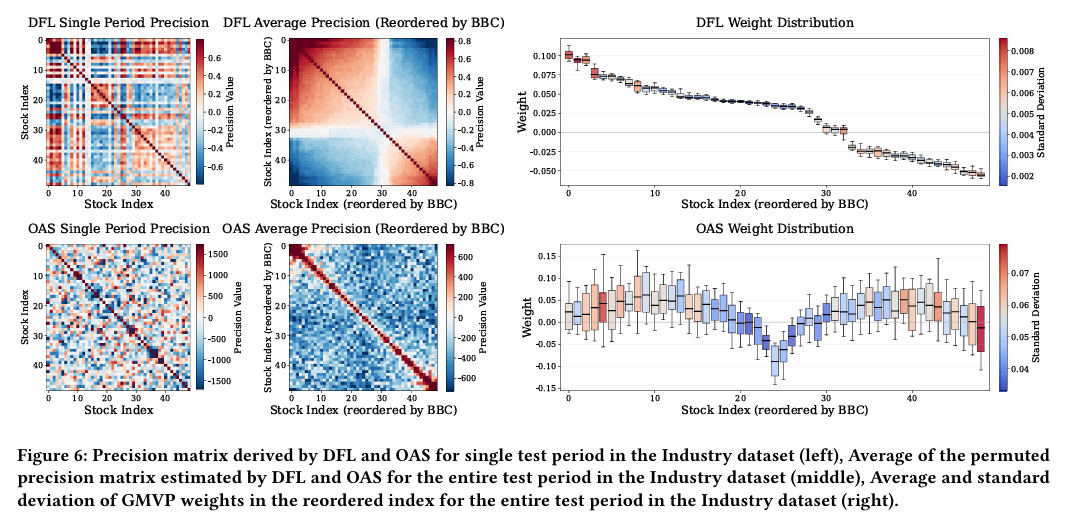
그림 6(왼쪽)은 테스트 샘플에 대해 DFL과 OAS로 추정한 정밀도 행렬의 히트맵을 나타낸다.
- DFL 기반 정밀도 행렬은 일관되게 높은 값의 행 그룹과 일관되게 낮은 값의 행 그룹이 뚜렷하게 나타나는 반면 OAS는 대부분의 행에서 낮은 값이 지배적이며 더 무작위적으로 보인다.
→ 따라서 이 논문에서는 DFL 정밀도 행렬의 적절한 행/열 순열이 높은 가중치 주식과 낮은 가중치 주식에 해당하는 블록 구조를 나타낼 것이라는 가설을 세운다.
이를 위해 BBC(Bidirectional Block Construction) 방법을 통해 분석을 진행한다.
BBC 알고리즘은 다음과 같이 이루어진다.
- 가장 큰 비대각 정밀도 값을 갖는 자산 쌍을 찾는다(가장 강하게 연결된 쌍).
- 이 둘을 왼쪽 위에 배치한다.
- 이 쌍과 가장 안맞는 자산을 찾는다.
- 이 자산을 오른쪽 아래에 배치한다.
- 남은 자산들을 양쪽 중 더 잘 맞는 쪽으로 배치한다.
그림 6(중앙 패널)은 순열된 DFL 정밀도 행렬을, 오른쪽 패널은 순열된 정밀도 행렬에서 계산된 평균 GMVP 가중치를 나타낸다.
- 왼쪽 위에는 높은 값의 뚜렷한 블록이 있고 오른쪽 아래에는 낮은 값의 블록이 있다.
- 반면 OAS 기반 순열은 명확한 블록 구조를 나타내지 않으며 불안정적인 가중치 시퀀스를 생성한다.
→ 이러한 결과는 DFL의 정밀도 추정이 안정적이고 블록 구조화된 가중치 배분을 유도하는 반면, OAS는 시간이 지나면서 덜 일관된 결정을 내린다는 것을 보여줌
따라서 DFL이 의사결정을 위해 공분산을 더 효과적으로 예측할 뿐만 아니라, 견고하고 저변동성 포트폴리오 가중치와 자연스럽게 맞는 정밀도 행렬 구조를 생성한다.
이후 포트폴리오 위험을 유발하는 자산을 식별하기 위해, 이 논문에서는 실제 공분산 하에서 임의의 포트폴리오 w의 실현 변동성을 분해한다.
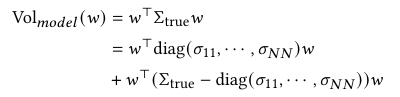
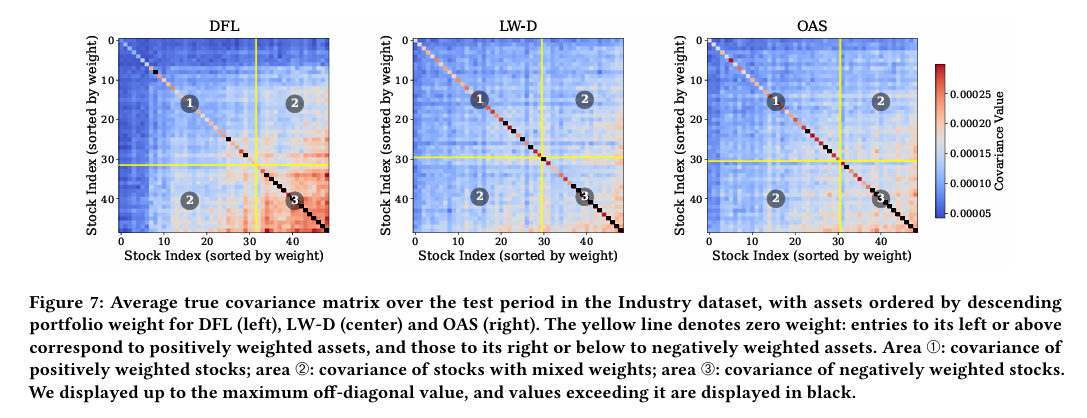
그림 7은 실제 공분산과 각 모델으로 추정한 공분산을 활용한 GMVP 가중치의 관계를 나타낸 그림이다.
히트맵은 테스트 기간 동안 포트폴리오 가중치를 내림차순하여 정렬했다.
- DFL 히트맵의 구간 1에서는 다른 모든 추정치보다 현저히 낮은 실제 공분산을 나타내며, 가중치가 큰 자산에서 특히 두드러진다.
- DFL은 극단적 포지션의 위험은 더 엄격히 평가하고, 중간정도의 포지션의 위험은 덜 엄격히 평가하면서 포트폴리오의 균형 효과를 만들어낸다. → 가중치가 한쪽으로 쏠리지 앟음.
- 반면 다른 추정치들은 이러한 구분이 나타나지 않으며, 이는 공분산 자체의 통계적 안정성에만 초점을 두었다는 것을 시사한다.
- DFL 추정치의 단점으로, 공매도 포지션 구간(구간 3)에서 DFL 실제 공분산이 다른 추정치보다 여전히 높은데 이는 상관관계가 높은 자산들이 서로 헤지가 되지 않고 함께 움직이면서 위험이 커질 수 있음을 의미한다.
→ DFL이 공분산이 높은(포트폴리오 가중치가 낮은) 자산에는 추정에 대한 엄격함이 덜하다는 것을 나타낸다.
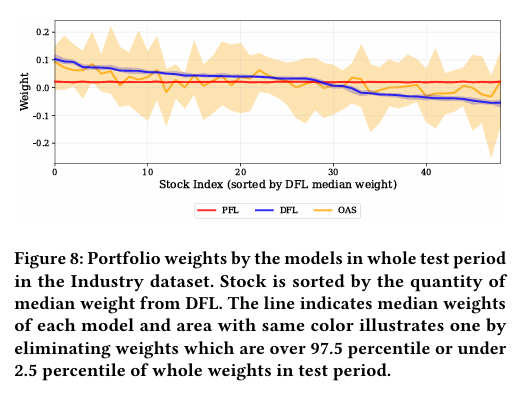
그림 8은 테스트 기간 동안 각 모델의 중앙값 포트폴리오 비중과 95% 구간을 보여준다.
- DFL은 PFL에 비해 포지션의 명확한 증가&감소를 나타낸다.
- DFL은 OAS와 다르게 일관된 패턴을 유지하며, 가중치 업데이트에 대한 안정성을 보인다.
→ 이는 DFL이 개별 자산의 특성을 식별하여 포트폴리오 할당을 결정한다는 것을 추측할 수 있음.
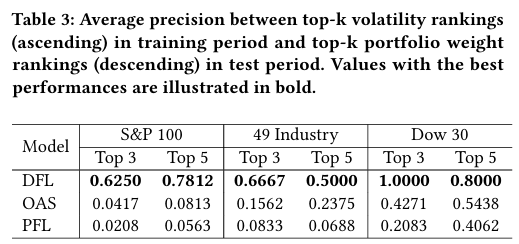
표 3에서는 위 그림 8에서 나온 결과에 대한 추측을 검증하기 위해 전체 학습 기간동안 실현 변동성을 기준으로 주식을 오름차순하고, 이러한 순위를 테스트 기간의 가중치 순위와 비교한 결과이다.
- DFL은 과거 변동성을 기반으로 한 롱 포지션 선택에서 높은 정밀도(Precision)을 나타낸다.
→ DFL이 체계적으로 낮은 변동성을 선택하는 자체 기준을 가지고 있음을 의미.
6. Conclusion
이 논문에서는 최소 분산 포트폴리오를 구성하기 위해 Decision-Focused Learning 프레임워크를 제안했다. 공분산 파라미터에 대한 decision-aware gradient의 주성분을 분석함으로써 DFL의 이론적 특성을 제시하였으며, 실증 분석을 통해 다른 추정 기법보다 포트폴리오 최적화 목표에 더욱 근접한 결과를 보였다.
따라서 DFL 기반 GMVP가 기존 추정 방법 및 PFL 대비 우수한 성과를 기록한다고 주장하며, DFL이 체계적으로 변동성이 낮은 자산을 선호하고 일관된 가중치를 주고 있다는 것을 보였다.
마지막으로 GMVP의 실제 구현에는 포트폴리오 기대수익률에 대한 부재와 공매도 허용에 대한 조건 때문에 어려움이 존재하는데, 향후 연구에서는 이러한 제약들을 포함하여 DFL의 실제 포트폴리오 배분 적용 가능성에 대한 실질적인 평가를 가능하게 할 수 있다고 언급한다.
7. 리뷰를 마치며
Dicision Focused Learning을 금융 분야에 적용한 논문을 처음 읽어보았는데 아주 유용하고 구조적으로도 효과적인 방법이라고 생각한다. 특히 포트폴리오 이론 중 MVO, GMVP와 같은 포트폴리오 이론은 몇몇 자산에 가중치가 쏠린다는 단점이 존재했는데 이러한 문제를 완화하면서도 추정 안정성 또한 높였다는 것이 매우 인상깊었다. 또한 단순히 포트폴리오 분산이 감소했다는 결과만 보여주는 것이 아니라 어떻게 모델이 작동하는지, 만들어진 포트폴리오의 각 자산의 가중치와 실제 공분산이 어떻게 매칭되는지 등을 보여주면서 분석의 강건성을 더욱 높여준 것 같다.
논문을 평가할 위치는 안되지만 감히 아쉬운 부분을 꼽아보자면, 이 논문을 읽어보면서 내가 이해한 바로는 포트폴리오 자산 유니버스의 각 자산들이 모두 동일한 공분산을 가지고 있다면 DFL과 PFL의 결과는 동일한 것이라고 보았다. 그렇다면 DFL 기반 GMVP 포트폴리오가 공분산이 서로 유사한 자산들과 서로 매우 다른 자산들 사이에서 얼만틈의 성능 차이를 보이는지(공분산 값이 서로 다른 자산군들일수록 GMVP 성능이 좋을 것으로 추측함)에 대해 추가적인 분석이 이루어졌다면 DFL이 GMVP에 미치는 영향 및 효과에 대한 해석을 한층 더 업그레이드 할 수 있지 않았을까 생각해보았다.