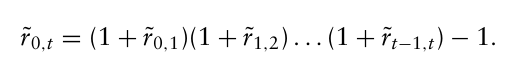최적화 스터디: Simulation Modeling
본 게시글은 『Simulation and Optimization in Finance』 원서를 바탕으로 주요 내용을 정리·해설한 글입니다.
Cahtper 4: Simulation Modeling
4.1 MONTE CARLO SIMULATION: A SIMPLE EXAMPLE
시뮬레이션 모델은 불확실성에 대한 확률 분포 가정을 입력으로 받아. 확률 분포로 설명되는 확률로 발생하는 시나리오를 생성.
→ 이러한 시나리오에서 관심 있는 변수의 변화를 기록 → 출력 확률 분포의 특성을 분석할 수 있음.
ex. 1000달러를 1년동안 미국 주식시장에 투자한다고 가정($C_0 = 1000$).
S&P 500 인덱스 펀드에 1년동안 투자할 경우 $\tilde C_1 = C_0 + \tilde r_{0,1}C_0$
이때 총 수익률은 다음과 같이 구할 수 있음.
$r_{t,t+1} = \frac{P_{t+1}-P_t+D_t}{P_t}$
$\tilde C_1$ 을 추정하기 위해서, 시장 수익률을 추정한 후 그 결과값을 사용할 수 있지만 이는 단일 점 추정치만 제공한다는 단점이 존재한다.
보다 정교한 접근법은 시장 수익률에 대한 연간 시나리오를 생성한 후, 각 시나리오에서 $\tilde C_1$ 를 계산하는 것.
이를 히스토그램으로 만들어 대략적인 확률 분포를 시각화하고, 통계적 측정치를 분석할 수 있다.
4.1.1 Selecting Probability Distributions for the Inputs
그렇다면 미래 가치에 대한 시뮬레이션 모델을 만들 때 가장 먼저 물어봐야 할 질문
→ “미래 시장 수익률을 모델링하는 데 어떤 분포가 가장 적합한가?”
가장 간단한 방법으로는, 과거 수익률의 역사적 분포가 미래에도 동일하게 행동할 것이라고 가정하는 것. 이후 미래 실현값에 대한 시나리오를 만들 때 역사적 시나리오에서 무작위로 샘플을 추출할 수 있음.
또다른 방법은 미래 수익률에 대해 특정 확률 분포를 가정하고, 역사적 데이터를 사용하여 매개변수(기댓값과 표준편차 등)를 추정하는 것(ex. 수익률이 정규분포를 따른다고 가정하면 역사적 수익률 변동성을 표준편차 측정값으로 사용할 수 있음.)
세번째 접근법은 특정 분포에서 시작하는 것이 아닌, 과거 데이터를 사용하여 가장 잘 맞는 수익률 분포를 찾는 것.
네번째 접근법은 미래만을 바라보며 모델에서 불확실한 변수가 어떻게 행동할지에 대한 주관적 추측을 기반으로 확률 분포를 구성하는 것.
이 4개 접근법 중 어느것도 정답이라고 할 수는 없음. 결국 핵심은 좋은 입력값을 제공하고 결과를 신중히 해석하는 데 있음.
4.1.2 Interpreting Monte Carlo Simulation Output
다음 1년동안 시장 수익률이 정규 분포를 따른다고 가정(두번째 방법 사용).
1977년부터 2007년까지 S&P500은 연평균 8.79%의 수익률을 기록했으며, 표준편차는 14.65% 이었음.
→ 이 값들을 다음 1년동안 주식시장 투자 수익률의 평균 수익률 & 표준편차에 대한 근사치로 사용
이 섹션에서는 다음 1년동안 시장 수익률에 대해 100개의 시나리오를 생성했을 때 얻을 수 있는 결과에 대해 논의한다.
평균 8.79%, 표준편차 14.65% 를 가지는 정규분포 하에서 100개의 숫자를 추출하면 다음과 같이 출력 그래프가 나타남.
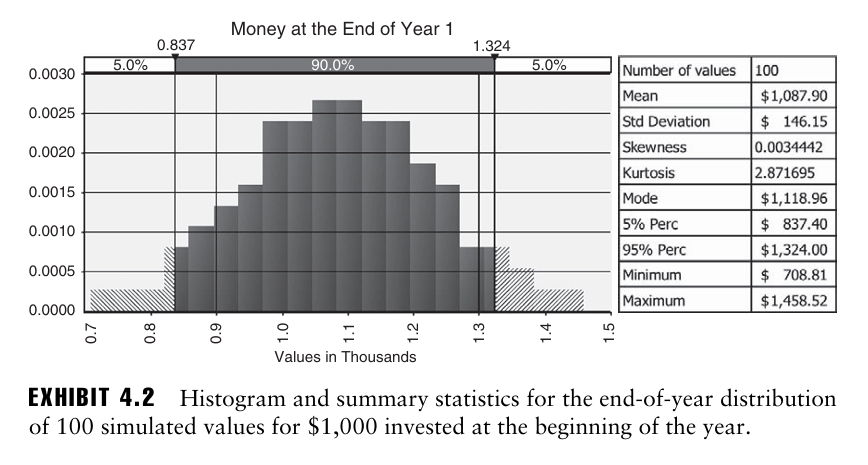
- 과거 추세가 지속된다면, 첫해 말에 평균적으로 $1087.9 를 갖게 될 것으로 예상됨.
- 연말 자본의 표준편차는 $146.15
- 5% 확률로 837 을 초과하지 못하며, 95% 확률로 1324 미만일 것.
- 왜도는 0에 가까우며, 첨도는 3에 가까움 → 이론적 정규분포의 왜도 첨도와 동일하기 때문에 시뮬레이션된 분포가 정규 분포에 가깝다는 것을 시사함
※ 주의점
이론적으로 시뮬레이션에서 얻을 수 있는 최소값과 최대값은 음의 무한대 & 양의 무한대임.
따라서 시뮬레이션에서 얻은 최소값과 최대값은 신중하게 해석해야 함.
시나리오가 생성되면, 각 시나리오 샘플의 평균을 추정할 때, 추정치의 정확성을 신경써야함.
→ 95% 신뢰구간 산출.
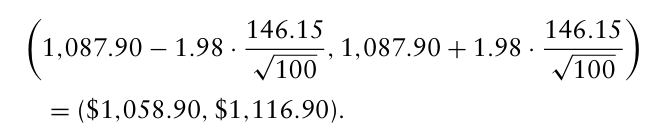
따라서 실제 연말 자본의 평균이 1058.9 ~ 1116.9 사이에 있을 확률이 95%라고 할 수 있음.
4.2 WHY USE SIMULATION?
4.1장에서 본 시뮬레이션의 장점: 확률 변수의 함수를 평가할 수 있게 해줌.
→ $\tilde C_1 = C_0 + \tilde r_{0,1}C_0$ 에서 r이 정규분포를 따르지 않아도 시뮬레이션을 통해 $\tilde C_1$ 의 경험적 분포를 얻을 수 있음.
이외에도 시뮬레이션은 세 가지의 장점이 존재하는데,
- 여러 입력 변수의 확률 분포를 결합한 결과로 발생하는 확률 분포를 시각화할 수 있음.
- 입력 변수 간의 상관관계를 반영할 수 있음.
- 저비용으로 특정 출력 변수에 대한 전략 변경 효과를 확인할 수 있음.
4.2.1 Multiple Input Variables and Compounding Distributions
이제 다음 해만이 아니라 30년 동안 시장에 투자하기로 결정했다고 가정하자.
초기 자본은 여전히 1000 이라고 가정하고, 30년 후에 얻게될 수익률($\tilde C_{30}$) 에 대해 관심을 가지고 있는 상황.
투자 수익률의 평균과 표준편차는 4.1.2장과 동일하다고 가정(8.79%의 수익률, 표준편차는 14.65%).
4.1.2장에서는 시뮬레이션을 통해 1년 말 자본의 확률분포가 정규분포임을 알 수 있었는데, 과연 30년 전체 수익률 및 30년 말 자본의 확률분포도 정규분포일까?
일반적으로 여러 입력 확률 분포를 다룰 때 기억하면 유용한 사실들은 다음과 같다.
- 상수 하나를 확률 변수에 더하면 분포는 같지만 평균은 1만큼 이동하게 됨
- 단순히 두 확률 분포를 더할 수는 없음(예외로 독립적인 두 정규분포를 더하는 것은 가능).
- 확률변수의 곱은 확률변수의 합보다 더 시각화하기 어려움(모든 확률변수가 동일한 확률 분포를 따른다고 해도 그 곱이 같은 확률분포를 가지는 경우는 거의 없음.).
→ 예외로 로그 정규분포의 경우 각 확률변수가 로그 정규분포를 따를 때 확률변수들을 모두 곱한 것도 로그 정규분포를 따르는데, 이는 정규분포의 합 특성 + 로그 특성으로 인해 가능한 구조. 이는 금융 모델링에서 로그 정규분포가 자주 사용되는 이유 중 하나라고 할 수 있음.
시뮬레이션은 이러한 확률 분포를 시각화하는 것을 쉽게 만들어준다.
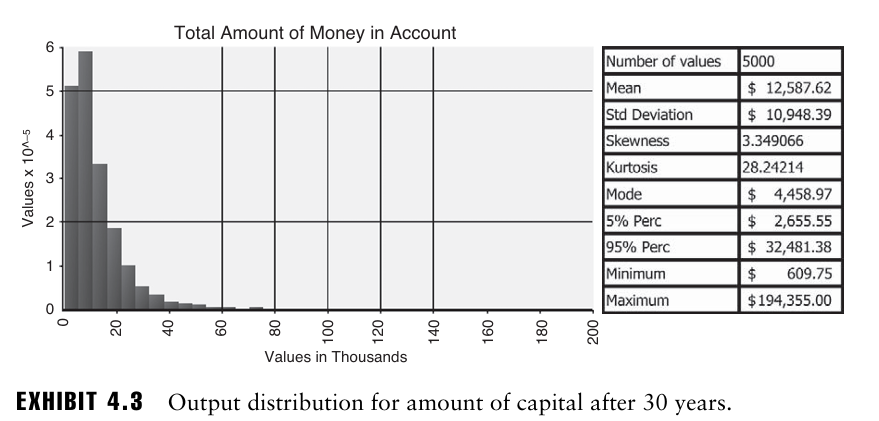
- 30년 후 총 수익과 자본의 출력 분포를 나타냄.
- 각 연도의 개별 수익 분포는 왜도가 0, 첨도가 3으로 정규분포와 매우 유사했음에도 불구하고 30년 전체 수익의 분포는 매우 왜곡되어 있음.
4.2.2 Incorporating Correlations
이번에는 30년동안 주식 뿐만 아니라 국채에도 투자 가능성을 열어둔다.
통계적으로 주식과 채권은 서로 음의 상관관계를 가지는 경향이 있는데, 이는 주식시장이 부진할 경우 투자자들이 일반적으로 채권과 같은 안전자산에 자금을 이동하는 경향이 있으며 주식시장이 호황일 경우에는 채권 비중을 줄이고 자금을 주식으로 옮기기 때문.
시뮬레이션에서는 입력값으로 상관 행렬을 지정하거나 관찰된 과거 데이터를 샘플링하여 공동 시나리오를 생성함으로써 여러 입력 변수의 영향을 동시에 시각화할 수 있다.
자본의 50%를 인덱스 펀드에, 50%는 채권에 투자하며, 30년동안 리밸런싱이 이루어지지 않는다고 가정하자. 또한 주식시장과 국채시장 수익률 간의 상관관계가 약 -0.2, 국채 연간 수익률이 평균 4%, 표준편차 7%인 정규분포를 따른다고 가정.

30년 동안 5000개의 시나리오를 생성한 후의 출력 분포를 나타낸 결과이다.
30년 후 가용 자본의 분포 형태는 4.3의 표와 유사하지만 변동성은 더 작게 나타난다.
4.2.3 Evaluating Decisions
주식-채권 분배를 5:5로 하는 것을 A, 3:7로 하는 것을 B라고 하고 30년 말 자본 분포를 평가해보자.
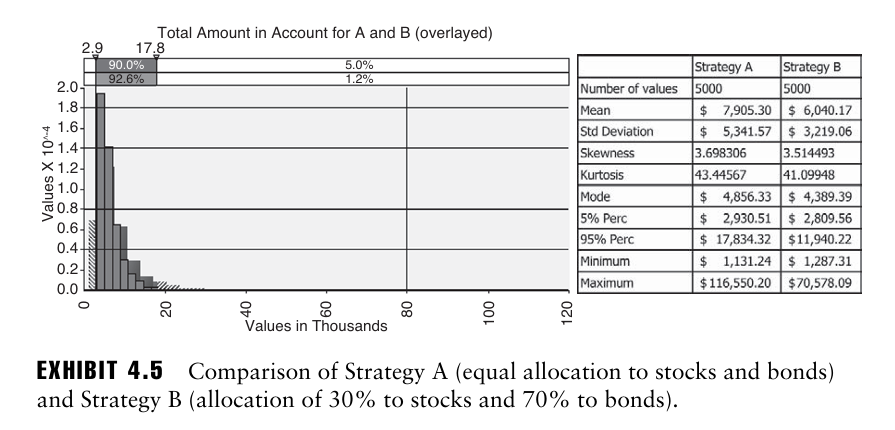
전략 A가 평균 수익에 있어서는 더 좋은 성과를 내는 반면, 그만큼 높은 표준편차를 가지고 있는 것을 확인할 수 있다. CV의 경우 A는 67.57%, B는 53.29%로 전략 A가 B보다 더 위험해 보인다.
그러나 분포가 정규분포가 아닌 비대칭 분포일 때 표준편차가 위험 측정 지표로 가장 적합하지 않을 수 있다.
→ 5번째 백분위수에서 A는 B보다 수익이 덜 나쁘고, 95번째 백분위수에서도 A가 B보다 수익이 더 좋음. 따라서 꼬리 위험만 보게 될 경우 A가 B보다 덜 위험할 수 있음.
즉 전략 A의 높은 표준편차의 원인은 큰 손실이 아닌 큰 이익으로부터 나오는 것이라고 할 수 있다. 이는 전략 A의 왜도가 약 3.7로 분포의 오른쪽 꼬리가 긴 형태로 나타나 이익의 극단값이 높기 때문에 발생한 것.
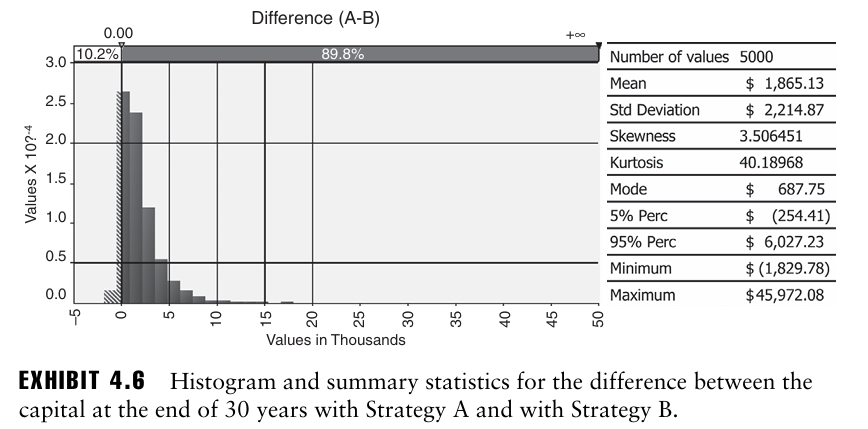
이번엔 전략 A와 전략 B를 시나리오별로 비교해보자.
B가 A보다 더 좋은 성과를 내는 시나리오는 몇퍼센트인가?
→ 효율적인 방법 중 하나는 difference 변수를 만드는 것
- 위 그림은 A-B의 히스토그램을 보여준다.
- EXIHIBIT 4.5에 따르면 A가 B보다 위험해 보였음에도 불구하고 5000개의 생성 시나리오 중 A가 B보다 실현 결과가 낮다는 것(10.2%만이 0보다 작은 값을 가짐).
※ 두 전략간 비교를 위해서는 두 전략 모두 동일한 시나리오를 사용하는 것이 좋음. 이는 우연히 발생할 수 있는 상황을 제거할 수 있기 때문.
4.3 IMPORTANT QUESTIONS IN SIMULATION MODELING
4.3.1 How Many Scenarios?
시뮬레이션이 모델 내의 모든 경우를 포착할 수는 없지만 매우 가까이 갈 수는 있음.
추정의 정확성은 생성 시나리오의 수에 따라 달라진다.
→ 시나리오 생성이 무작위라면, 표준오차는 $\frac{s}{\sqrt N}$ 이 되며, s는 출력 변수의 시뮬레이션 값의 표준편차, N은 시나리오 수를 의미함.
4.2장의 예시를 가져오면, 100개의 시나리오에 대해 1년 후 평균 자본은 $1,087.90 이며, 95% 신뢰구간은 (1058, 1116.9)였음.
→ 만약 표본평균 및 표본 표준편차는 같은 수치인데 시나리오 수가 400으로 4배만큼 증가했다고 가정하자.
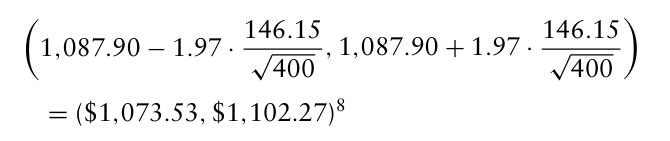
이는 시나리오 수가 100개일 때보다 구간이 절반정도로 줄어든 것을 확인할 수 있음.
따라서 복잡한 다기간 상황의 경우에는 정확도를 높이기 위해 시나리오 수를 증가시키는 것에 대한 계산 비용이 많이 들 수 있다.
또한 시뮬레이션 결과로 보는 지표 중 대표적인 것이 기대값인데, 금융에서는 기대값보다 백분위수와 같은 꼬리 위험에 관심을 가지는 경우가 많다.
근데 이러한 꼬리 위험, 백분위수 추정은 시뮬레이션에 있어서 훨씬 어려움(데이터가 적고 분포에 민감하기 때문). → 부트스트랩이 하나의 대안이 될 수 있긴함.
그렇다면 출력 분포를 잘 나타내기 위해 얼마나 많은 시나리오를 생성해야 하는가?
→ 정확한 답은 없음.
이는 확률 이론의 결과가 실제로 사용되는 시나리오 생성 방법에는 반드시 적용되지 않는다는 사실 때문에 더욱 복잡해지는데, 순수하게 무작위 표본을 시뮬레이션하는 이론과는 달리 우수한 추정 정확도를 위해 스마트 샘플링을 사용하기 때문.
4.3.2 Estimator Bias
추정치 편향(estimator bias)는 시뮬레이션 응용에서 중요한 개념이다.
이는 추정치가 평균적으로 올바르게 추정되는지, 즉 충분한 수의 반복을 거쳤을 때 실제 모수를 근접하게 추정하는지를 보여줌.
→ 시나리오 표본에서 얻은 평균은 불편추정량(표본이 증가할수록 실제 평균에 가까워지기 때문).
그러나 시나리오를 생성하는 방식에 따라 관심 있는 모수의 추정치에 편향이 도입될 수 있다.
편향의 크기는 추정한 평균값과 모수의 차이에 의해 결정되며, 이는 표본 수가 적어서 생기는 랜덤 오차가 아닌 표본을 무한히 늘려도 남는 구조적인 오차를 의미한다.
4.2.1 예제에서, 초기자본 1000에 매년 수익률을 적용해서 30년 후 자산 분포를 계산했는데 실제로는 연 1회가 아니라 훨씬 더 자주 복리가 이루어져야 한다.
→ 연속적인 시간에서 가격 변화가 이루어지는데 이를 이산적으로 연 단위로 점프했기 때문. 여기서 편향이 생기며 이를 이산화 오류 편향이라고 한다.
파생상품의 경우 고정 드리프트와 변동성이 있는 기하학적 브라운 운동(GBM)을 통해 연속 시간 공식으로 미래 자산 가격을 시뮬레이션함으로써 평균 금융 파생상품 수익의 불편추정량을 얻을 수 있지만. 많은 경우는 미래 자산 가격에 대한 closed-form 표현식을 찾는 것이 불가능하다.
→ 이 경우 시간 간격을 줄여 편향을 줄일 수 있지만, 시간 간격을 줄이게 되면 미래 자산 가격에 대한 무작위 경로를 생성하는 데 필요한 단계 수가 늘어나고, 계산 비용이 많이 들게 됨.
4.3.3 Estimator Efficiency
편향에 대한 조건이 모두 동일한 두 추정치 중에서 무엇을 더 선호하는가?
→ 어떤 추정치가 더 효율적인가?
각 추정치의 표준오차는 다음과 같다.
$\frac{s_1}{\sqrt{N_1}}$ and $\frac{s_2}{\sqrt{N_2}}$
통계 이론에 따르면, 표준편차 s가 더 작은 추정치를 선택하는 것이 바람직하다.
그러나 시뮬레이션의 경우, 이러한 통계적 개념에서 수치적 및 계산적 고려사항을 포함할 수 있다.
ex. A가 B보다 표준편차가 더 작음. 그러나 시나리오 생성에 있어서 시간이 더 오래걸린다면, 차라리 B를 추가시간을 사용해서 시나리오를 더 많이 생성하는 것이 좋지 않은가?
$τ_1$, $τ_2$ 를 각각 두 추정치의 시나리오 하나를 생성하는 데 걸리는 시간이라고 하면, 시간 조정된 표준오차 $s_1 \sqrt{τ_1}$, $s_2 \sqrt{τ_2}$ 중에 더 작은 값을 선택해야 한다.
4.4 RANDOM NUMBER GENERATION
4.4.1 Inverse Transform Method
0과 1 사이의 임의의 수를 목표하는 확률 분포의 수로 변환하는 일반적인 방법은 연속 균등 분포에서 생성된 임의의 수에서 누적 확률 분포 함수의 역함수를 평가하는 것이다.
이는 확률 분포의 전체 합이 항상 1이고, 분포의 임의의 값에 대한 누적 확률이 항상 0~1에 존재하기 때문.
먼저 CDF 상에서 y좌표가 0~1 사이인 난수에 해당하는 점의 x좌표를 찾으면, 이를 시뮬레이션 값으로 사용한다. 이 과정을 반복하면 목표한 분포가 만들어짐.
The Inverse Transform for Discrete Distributions
값 5를 갖는 확률 50%, 15를 갖는 확률 30%, 35를 갖는 확률 20%가 되는 확률 분포를 시뮬레이션 하고 싶다고 가정하자.
이 확률 분포의 CDF는 다음과 같다.
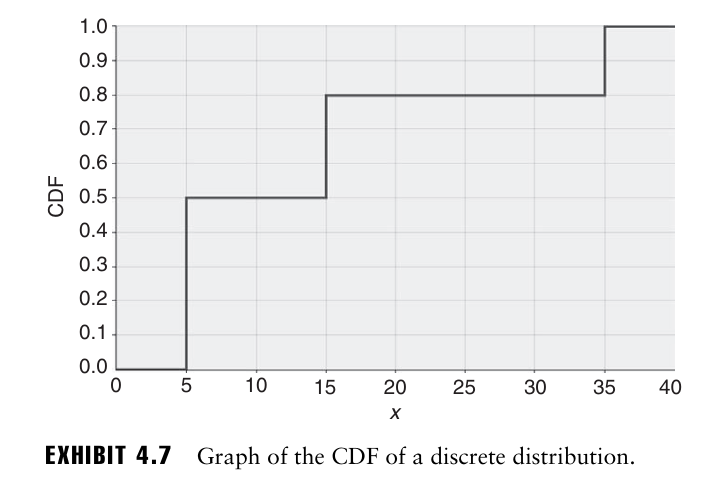
균등분포에서 추출한 무작위수가 구간 [0,0.5]에 속할 경우 값 5를, [0.5,0.8]에 위치할 경우 값 15를 기록한다.
The Inverse Transform for Continuous Distributions
일부 확률 분포는 CDF의 역함수에 대한 closed-form 표현식을 가지고 있다.
대표적인 예시로 지수분포가 있는데, 지수분포의 PDF는
$f(x) = \lambda e^{-\lambda x}$ , $x \geq 0$
이를 통해 지수분포의 CDF를 계산할 수 있다.
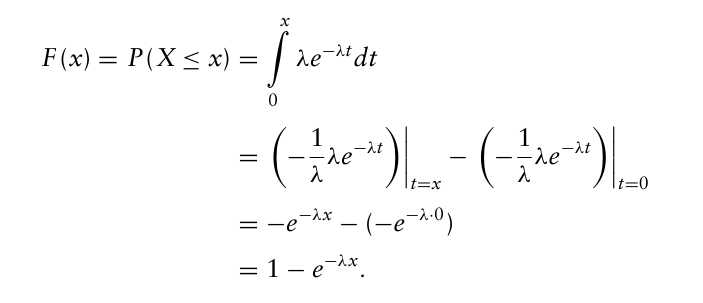
이 CDF의 역함수를 구하면,
$e^{-\lambda x} = 1 - F(x)$
$x = - \frac{1}{\lambda} ln(1-F(x))$
추가적으로 평균 $\mu$ 와 표준편차 $\sigma$ 를 갖는 정규분포를 생각해보자.
예를들어 균등분포의 난수로 0.975가 나왔다면 이는 정규분포의 97.5%에 해당하는 값을 의미한다.
그러나 지수분포와 달리 정규분포는 CDF의 역함수에 대한 닫힌 형태의 해가 없다.
따라서 누적 정규분포 함수의 역함수를 근사하거나,
- The acceptance-rejection method
- The composition method
- The ratio of uniforms method
등의 방법이 존재한다.
이외에도 정규분포의 경우 단변량 및 다변량 정규 확률 변수의 효율적인 시뮬레이션을 위한 방법들이 개발되었는데, Box-Muller 알고리즘과 Beasley-Springer-Moro 방법론이 존재한다.
4.4.2 What Defines a “Good” Random Number Generator?
원하는 확률 분포로 변환하기 위해 좋은 균등 난수를 생성하는 것은 시뮬레이션 알고리즘 성능에 매우 중요하다.
초기에는 진짜 랜덤 추출을 하려 했으나 현실적으로 매우 느리고 측정 비용이 컸음. 또한 재현이 안된다는 단점이 존재했다.
대부분의 시뮬레이션 소프트웨어는 무작위로 보이는 숫자 스트림을 생성하는 난수 생성 알고리즘을 사용하지만, 실제로 난수는 명확하게 저의된 일련의 계산 단계의 결과로 나타난다.
$x_n = g(x_{n-1})$
이는 시드(seed)라는 숫자에 의해 발생되며, 따라서 동일한 시드 값을 사용하면 시뮬레이션 시퀀스는 정확히 동일한 숫자를 포함하므로 전략 간 공정한 비교가 가능하게 한다.
이러한 재귀 공식(의사난수 생성기)이 무작위 행동을 잘 모방한다는 것은 Gilvenko-Cantelli 이론 및 CLT와 같은 법칙을 따른다는 것을 통해 알 수 있다.
일반적으로 의사난수 생성기는 다음 조건을 충족할 때 좋은 것으로 간주된다.
- 생성된 수열의 숫자들에 대해 카이제곱 검정 혹은 KS 검정을 통해 균등하게 분포되어 있는지 확인
- 수열이 긴 주기를 가지고 있음
- 수열의 숫자가 자기상관되지 않음. 이는 Durbin-Watson 검정으로 확인 가능
4.4.3 Pseudorandom Number Generators
가장 초기의 의사난수 생성기 중 하나는 midsquare technique 이라고 부르는데, 시드를 제곱한 후에 중간 자리 숫자 집합을 다음 난수로 사용하는 방식이다.
ex. 시드가 5381이라고 가정하자.

※ 시드 제곱값이 홀수면?
관행적으로 앞에 0을 붙여서 짝수 자릿수로 맞춤.
그러나 이 방식은 중간 자리수가 1 또는 0과 같은 수가 되는 순간 그 이후의 수열들은 반복적으로 생성되버린다.
이러한 문제를 해결하는 의사난수 생성기로 나온 것이 합동 의사난수 생성기(congruential pseudorandom number generators).
$x_n = g(x_{n-1})$ mod $m$
여기서 mod m은 “modulus m”을 의미하며, $x_n = g(x_{n-1})$ mod $m$ 은 $x_n = g(x_{n-1})$ 을 m으로 나눈 나머지를 의미한다.
이는 항상 0과 m-1 사이의 정수로 나타나기 때문에 좋은 난수 표현을 만들기 위해서는 m의 범위를 가능한 한 크게 하는 것이 좋다.
예시로 선형 합동 의사난수 생성기를 보자.
$x_n = Ax_{n-1}$ mod $m$
→ $x_n = A x_{n-1} - m \left\lfloor \frac{A x_{n-1}}{m} \right\rfloor$
이때 $x_0$ 은 시드를 나타낸다.
A = 3, m = 10, seed = 1052 라고 가정하자.
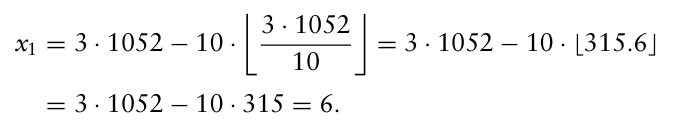
→ 난수값은 0.6
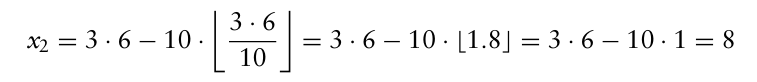
→ 난수값은 0.8
이외에도 더 발전된 다양한 난수 생성기들이 존재한다.
- Linear congruential generators (LCGs).
- Multiplicative recursive generators (MRGs)
- Feedback shift registers (FSRs).
- Generalized feedback shift registers (GFSRs).
- Combined multiplicative recursive generators (CMRGs)
- Twisted generalized feedback shift registers (TGFSRs).
- Add-with-carry (AWC) and subtract-with-borrow (SWB) generators.
- Inversive generators (IG).
현재 대중적인 소프트웨어에서 사용되는 대부분의 의사난수 생성기는 우수한 성능을 보이지만, 시뮬레이션 용도로 만들어지지 않은 소프트웨어 패키지의 의사난수 생성기는 전문 시뮬레이션/소프트웨어의 난수 생성기만큼 우수하진 않다.
4.4.4 Quasirandom (Low-Discrepancy) Sequences
진정한 난수 생성기는 군집화된 관측값을 생성할 수 있으며, 이는 관심 있는 출력 분포를 잘 나타내기 위해 많은 시나리오를 생성해야 함을 의미한다.
반면 준난수(quasirandom) 시퀀스는 이전에 생성된 난수가 남긴 단위 구간의 공백을 지속적으로 채움으로써 범위를 부드럽게 나타낸다.
→ 의사난수 생성기와는 달리 준난수는 무작위라고 볼 수 없음. 의도적으로 값을 채우는 형태이기 때문. 따라서 quasirandom 대신 low discrepancy라고 부르는 경우도 많음.
대표적인 준난수 시퀀스로는 Sobol(1967), Faure(1982), Halton(1960), Hammersley(1960) 등이 존재하며, 이러한 수열은 Van der Corput 수열 계열을 기반으로 한다.
※ Van der Corput 수열?
정수를 2진수로 바꾼 다음, 그걸 거꾸로 뒤집어서 소수로 만든 후에 10진 값으로 표시.
특히 Faure, Sobol 수열은 매우 정확한 추정치를 생성하는 것으로 입증되었다.
4.4.5 Stratified Sampling
시뮬레이션의 실행 속도와 정확도를 높이기 위해서 다양한 분산 감소 기법들이 사용된다.
이 섹션에서는 @RISK와 같은 일부 시뮬레이션 소프트웨어 패키지에서 기본 표본 추출 방법으로 사용되는 층화 샘플링에 대해 소개한다.
※ 층화 표본 추출(stratified sampling)?
유사한 특성을 가진 집단으로 모집단을 나누어 대표 표본을 수집함으로써 전체 모집단을 더 잘 대표하도록 하는 방법
- 이는 최종 샘플에 모든 중요한 그룹이 포함되도록 보장함.
- 준난수 생성기와 유사하게 군집화 관측 문제를 해결하는데에 도움을 줌.
- 의도적으로 추출함에도 불구하고 어느정도 무작위성을 유지함.
- 정확도를 높일 뿐만 아니라 극단적 관측값을 시뮬레이션에 포함시키는 데에도 도움이됨.
→ 시나리오 수를 크게 늘리지 않아도 금융 분야에서 특히 중요한 꼬리부분 데이터를 반영해줄 수 있다는 것
다차원(여러 변수에 대한 난수)의 경우, 각 구간을 더 작게 나누어 hypercube를 만들고 각 hypercube에서 하나씩 추출할 수 있음.
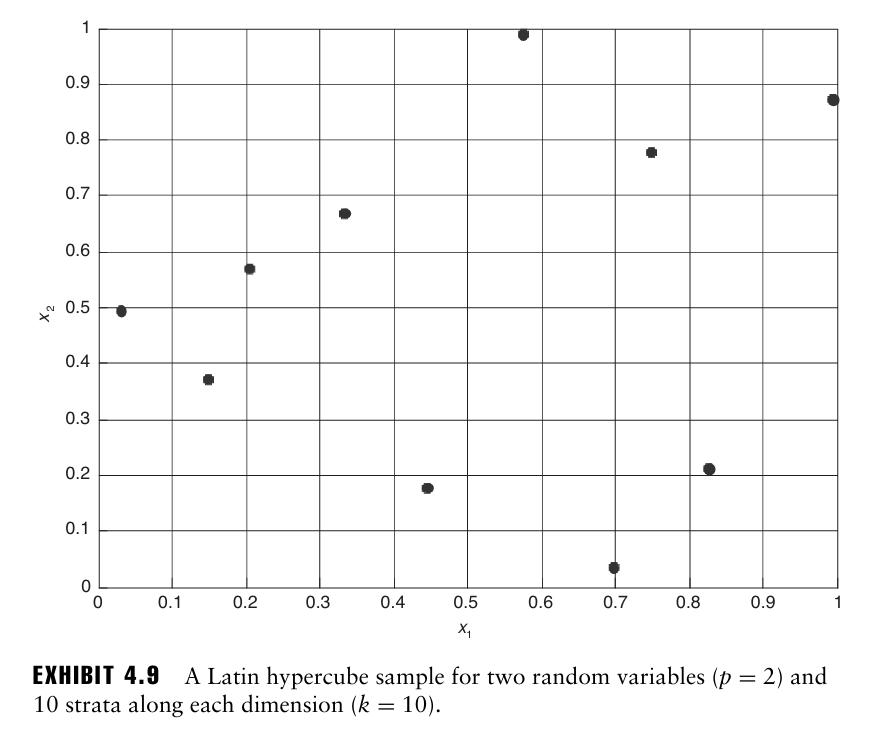
그러나 이 경우 각 p차원에 대해 k개의 구간이 있으면 이는 $k^p$ 만큼의 난수를 시뮬레이션해야 하기 때문에 계산 비용이 많이 든다는 단점이 존재한다.
이러한 층화 샘플링 방법을 개선한 확장 기법이 Latin Hypercube Sampling
이는 처음 생성된 난수 벡터 관측치의 좌표를 순열하여 실제 난수 생성 횟수를 줄이면서 모든 층이 충분히 대표되도록 한다.
- 각 차원에 따라 각 작은 구간 내에서 난수를 생성
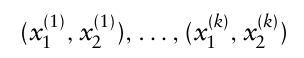
- 각 차원에서 점들의 좌표 순서를 서로 섞는다.
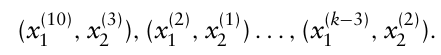
→ 이를 통해 $k^p$ 개의 난수를 생성하지 않고 $k \times p$ 개의 난수만 생성하여 층화 샘플링 수행 가능.
이러한 좌표의 모든 가능한 순열을 고려한다면 모든 하이퍼큐브에 대한 난수를 만들어낼 수 있다.
※ (개인적인 생각) 기존 층화 샘플링과는 다르게 LHS는 처음 생성한 난수는 고정한 상태로 조합만 바꾸는데 더 좋은 샘플링이 가능한것인가?